基于复杂网络理论的P2P覆盖网拓扑结构研究

郑力明,李哓冬,孙伟东

（1.国防科技大学 计算机学院 并行与分布处理国家重点实验室，湖南 长沙 410073；2.武警成都指挥学院 信息技术教研室，四川 成都 610213；3.武警成都指挥学院 科研科，四川 成都 610213）

随着网络技术的发展，计算机网络的规模越来越庞大，基于网络的应用中节点的规模也越来越庞大，传统的集中式客户端/服务器C/S（Client/Server）模式的应用模式因为存在可扩展性低、抗毁性差以及存在单点瓶颈等问题，逐步被分布式的对等端到端P2P（Peer-to-Peer）模式的应用所替代，因此，传统的随机网络模型已很难对其拓扑特性做出客观的描述。复杂网络理论以规模的网络系统为研究对象，其不断发展的理论和取得的成果为计算机网络拓扑的研究提供一个新的视野和思路。这里研究基于复杂网络理论的P2P覆盖网拓扑结构。

1 P2P覆盖网简介

P2P的本质思想在于打破传统的C/S模式，让一切网络成员享有自由、平等、互联的功能，不再有客户、服务器之分，任何两个网络节点之间都能共享资源、传递消息。在对等网络中，每个网络节点在行为上是自由的，在功能上是平等的，在连接上是互联的，因此，它能够极大程度地提高网络效率，充分利用网络带宽，开发每个网络节点的潜力。图1表示C/S模式与P2P模式的区别。

图1 C/S模式与P2P模式的区别

覆盖网（overlay）是在物理网络上构建的连接网络所有节点的逻辑拓扑结构，是P2P网络的核心机制。覆盖网的结构往往和应用相关，对应用系统的性能和效率具有决定性的作用。图2表示物理网络和覆盖网的关系。

2 复杂网络理论

2.1 网络定义

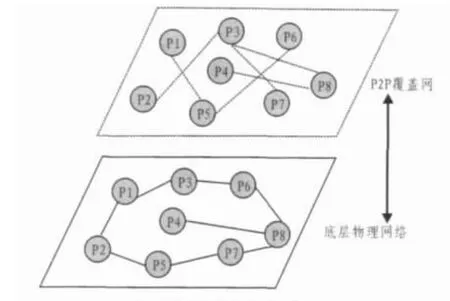
图2 P2P覆盖网示意图

网络是由许多节点与连接两个节点的一些边组成的，其中节点代表系统中不同的个体，边则表示个体间的关系。两个节点之间具有特定的关系则连接一条边，有边相连的两个节点被看作是相邻的。计算机网络可看作是自主工作的计算机通过各种物理介质与通信协议相互连接所得到的网络。

2.2 网络的统计参数

2.2.1 度和度分布

一个节点与其他节点相连的边数称为该节点的度，度是描述网络局部特性的基本参数。节点的度分布是指网络中度为k的节点的概率p（k）随节点度k的变化规律。节点的度分布函数反映网络系统的宏观统计特征，理论上利用度的分布可计算出其他表征全局特征参数的量化行为。

2.2.2 网络的平均距离L

在具有N个节点的网络中，两点i和j的距离定义为所有连通i到j的通路中，所经过的其他顶点最少的一条或几条路径的长度。网络的平均距离L定义为平均距离描述节点对时间的平均分离。

2.2.3 聚集系数C

在具有N个节点的网络中，若第i个节点的度为Ki，在由这ki个邻居节点构成的子网中，实际存在的边ei与这ki个节点所构成的完全图的总边数（ki（ki-1））/2的比值C（i）=2ei/（ki·（ki-1）），称为第i个节点的聚集系数。整个网络的聚集系数C定义为所有节点聚集系数的平均值，即集系数反映网络的聚集程度，聚集程度的意义是指网络集团化的程度，即网络的内聚倾向。

2.3 复杂网络的统计特征

复杂网络的主要统计特征是小世界效应（small-world effect），无标度性（scale free property），并且节点度服从幂律分布(power-law distribution)。研究表明，规则网络具有大的簇系数和大的平均距离，随机网络具有小的簇系数和小的平均距离。Watts和Strogatz通过以某个很小的概率p切断规则网络中原始的边，并随机选择新的端点重新连接，构造出一种介于规则网络和随机网络之间的网络（WS网络）。WS网络同时具有大的簇集系数和小的平均距离，因此既不是规则网络也不是随机网络[1]。随后，Newman和Watts给出一种新的网络构造方法，在他们的网络（NW网络）中，原有的连接边并不会被破坏，平均距离的缩短源于以一个很小的概率在原来的规则网络上添加新的连接边[2]。大的簇系数和小的平均距离两个统计特征被合称为小世界效应[3]，具有这种效应的网络就是小世界网络（small world networks）。图3是小世界网络的演化过程。

图3 小世界网络的演化过程

大量实验研究表明，真实网络几乎都具有小世界效应[4]，真实网络的节点度服从幂律分布[5-6]。幂函数曲线是一条下降相对缓慢的曲线，这使得度很大的节点可以在网络中存在。对于随机网络和规则网络，度分布区间非常狭窄，几乎找不到偏离节点度均值较大的点，故其平均度可被看作是其节点度的一个特征标度。则可把节点度服从幂律分布的网络叫做无标度网络（scale free networks），并称这种节点度的幂律分布为网络的无标度特性。Barabási和Albert把真实系统通过自组织生成无标度的网络归为两个主要因素：生长和优先连接，他们模拟这两个关键机制设计出构造无标度网络的演化模型（BA 网络）[7-8]。

3 P2P覆盖网拓扑结构

覆盖网是构建在一个或多个网络上的逻辑网络拓扑，它通过虚拟链路或逻辑链路连接网络节点，为应用提供与底层网络透明的网络访问接口。按照节点间的耦合度，现有覆盖网拓扑结构可分成结构化和非结构化两种。结构化拓扑通常以严格的规则确定节点之间的邻居关系和数据的放置位置，因此路由效率较高、开销较小，但维护开销较大，对网络的动态性支持不够；非结构化拓扑以一种松散的、随意的方式组织节点，因此构建简单，易于扩展，而且具有很好的鲁棒性，但是路由的效率较低、开销较大。

3.1 非结构化拓扑

在非结构化拓扑中，节点间的逻辑拓扑关系通常较为松散，具有较大的随意性。“非结构化”指覆盖网没有固定、严格的拓扑结构，是一张随机生成、松散组织的普通图或随机图，但理论上随机图可以是任何形状的。经典的非结构化网络有Genutella[9]和FreeNet[10]。非结构化拓扑的构建和维护相对简单，易于扩展并具有较强的鲁棒性。但由于其拓扑结构组织较为松散，节点及数据定位较为困难，通常采用泛洪搜索、随机搜索和选择性转发等方法，其效率和准确率难以保证，且冗余消息较多，网络开销也较大。

3.2 结构化拓扑

在结构化拓扑网络中，节点间的邻居关系通常由确定性的算法严格控制，资源(或资源的元信息)的放置也是由确定性的算法精确发布到特定的节点上。结构化拓扑通常采用分布式哈希表技术DHT（Distributed Hash Table）构建。典型的结构化覆盖网有 Chord[11]、Pastry[12]、CAN[13]等。常度数 P2P 网络是一种新型结构化覆盖网，其路由、定位、自组织方式与传统的模型区别并不大，但每个节点的“度”（即连接数）是固定的，不随网络规模改变，从而在保证数据查询效率的同时减少网络的自适应开销。常度数覆盖网有Viceroy[14]、Koorde[15]、Cycloid[16]等。

3.3 基于复杂网络理论的拓扑结构

传统的覆盖网构建主要研究资源的查询、定位、分发效率等问题，很少从网络的本质属性出发研究覆盖网的特征。随着复杂网络理论研究的逐步成熟，基于复杂网络理论的拓扑研究逐渐成为覆盖网拓扑结构研究的热点。网络是一个不断变化的动态系统，因此掌握网络拓扑行为的演化规律是网络动态覆盖网构建的基础。传统方法大都采用结构相对简单的随机网络[17-18]描述真实的计算机网络拓扑。在规模不大、业务种类比较单一的网络初步阶段，随机网络模型在一定程度上能客观反映计算机网络拓扑演化规律。

随着计算机网络规模和用户数量巨大且不断增长，各种异构的网络需要融合发展、共享资源；网络协议体系庞杂，垂直方向呈现出多样化的层次结构，而水平方向上又以地域和功能为标准进一步形成分布且多级的架构；网络节点间、节点与数据分组间由于协议而产生的非线性作用、用户之间的合作与竞争，这些情况使计算机网络日益复杂。强调系统整体性的复杂网络理论提供了计算机网络拓扑研究的新思路。利用复杂网络理论研究计算机复杂的网络行为，从多个视角、不同抽象角度分析网络系统，研究各个单元之间相互连接、相互作用而导致网络系统表现出的行为规律和本质。例如流量行为特性分析、网络拓扑的生成机理和动力学行为、流量行为和拓扑行为的相互作用、网络同步行为的研究等。

3.4 计算机网络拓扑行为的演化模型

针对计算网络拓扑，主要是基于复杂网络演化模型（BA模型）及其改进型的局部演化模型，从路由器和自治域两种不同层次描述计算机网络的拓扑结构[19-21]。从路由器层次看，路由器相当于网络节点，路由器之间的物理连接相当于边；而从自治域看，如果两个自治域之间存在基于边界网关协议（BGP）的对等连接，则表示这两个节点之间有一条边相连。研究表明，计算机网络的增长遵循BA模型的“偏好连接”法则，演化的结果会导致“富者更富”的现象，即新加入的用户总是更倾向于优先考虑连接到那些知名度高、服务质量好、连接数多的服务器或网络服务商。但这个模型明显的不足之处是，其中的“偏好连接”是基于整个网络的“偏好连接”，这点与实际情况不符，现实中网络路由一般优先考虑连接到本地区的路由器或服务器，即使该地区以外的其他路由器或服务器的连接数可能要高于当地路由器的连接数。针对这种情况，Wang等人所提出的局部演化模型的“偏好连接”的倾向性[22]是基于局部而非全局的信息，在一定程度上改进该模型的缺陷。

现有的模型还不能很好地解释计算机网络拓扑演化规律。无论是BA模型、局部演化模型还是其他演化模型，都是在一些理想化的简单假定下解释计算机网络复杂的拓扑演化规律的，对于在一些复杂情况下（诸如信息传输中的延迟、时变、节点动态加入和退出、不同节点不同动力学的差异等）网络拓扑行为特性的研究较少，所以现有的模型还不能很好地描述网络拓扑对网络动力学的影响以及网络单节点的行为与网络整体行为特性的关系等问题。而能更加真实的细致和全面的刻画计算机网络拓扑结构的动力学演化特性的模型还有待研究[23]。

4 结束语

计算机网络庞大的规模、异质而复杂的体系结构和丰富的动态特性，使传统的随机网络模型难以对其拓扑行为特征做出系统、客观的描述，强调系统整体性的复杂网络理论为网络行为的研究提供了新方法，成为解决网络行为基础理论研究的有力工具，为网络的基础理论研究带来重大突破。任何复杂网络理论研究的新成果都有可能被运用到计算机网络行为特性的研究中，结合计算机网络的特点，应用复杂性理论研究计算机网络的拓扑行为，有可能发现其拓扑行为演化规律，从而根据实际需要，设计出性能较优越的计算机网络。 以下是基于复杂网络理论的计算机网络拓扑行为以及相关技术可以研究的方向和实现的目标：

1）从理论上定义和建立计算机网络的复杂网络理论。包括描述计算机网络拓扑基本性质的特征量，定量与定性分析方法；研究计算机网络的拓扑演化机制，不同节点对于整个网络拓扑演化行为的影响程度，以及彼此间的相互作用；寻求能够真实反映其拓扑结构的复杂网络的构造机制，并建立网络拓扑以及其动力学演化行为的模型，基于该模型讨论网络结构的统计平均性质，如类似节点度的分布特征、小世界性质、无标度特性以及动力学过程中混沌、分形等复杂行为；构造网络拓扑模型的各种算法以及模型的性能评价。

2）基于复杂网络的某些统计特性，研究计算机网络拓扑的构建、拓扑发现、用户的动态更新、资源管理、服务发现、服务部署等问题；针对某种具体网络体系结构服务或应用，构造其相应的性能高、可扩展性好、有利于管理的具有小世界或无标度特性的网络结构，如具有小世界特性或无标度的主动网络、主动Overlay网络、Web服务Overlay网络、P2P网络、组播Overlay网络。

3）基于复杂网络理论的路由机制及其算法的研究，以及如何通过适当的路由机制提高网络的信息传输量。

4）基于复杂网络理论探讨了计算机网络的可靠性、抗毁性，提出一个能够真实描述计算机网络鲁棒同时脆弱的动力学模型。

5）在复杂网络理论中引入节点带宽、网络延迟等物理网络特性，优化拓扑结构。

[1]Watts D J,Strogatz S H.Collective dynamics of small-world networks[J].Nature,1998（393）：440-448.

[2]Newman M E J.Models of the small world[J].Phys.Rev,1999（60）：7332-7336.

[3]Watts D J.Networks,dynamics,and the small world phenomenon[J].Amer.Sociol,1999:493-499.

[4]Sen P,Chakrabarti B K.Mall-world phenomena and the statistics of linear polymers[J].Phys，2001:7749-7753.

[5]Faloutsos M,Faloutsos P,et al.On power-law relationships of the internet topology[J].Computer Communications Rev,1999（29）：251-255.

[6]Ebel H,Mielsch L I.Scale-ree topology of e-mail networks[J].Phys.Rev,2002（26）：035103-035110.

[7]Barabási A-L,Albert R.Emergence of scaling in random networks[J].Science,1999（286）：509-513.

[8]Barabási A-L,Albert R,etal.Mean-field theory for scale free random networks[J].Physica A,1999（272）：173-179.

[9]Gnutella protocol specification[EB/OL].2001.version 0.4Http://www.clip2.com/GnutellaProtocol04.pdf.

[10]Clarke I,Sandberg O,Wiley B,et al.Freenet.A distributed anonymous information storage and retrieval system[C]//InPr oc.of ICSI Workshop on Design Issues in Anonymity and Un observability.Berkeley,2000.

[11]Stoica I,Morris R,Liben-nowell D,et al.A scalable Peer-topeer lookup protocol for internet applications[J].IEEE/ACM Transactions on Networking,2003（11）：17-25.

[12]Rowstron A,Druschel P.Pastry.Scalable,distributed object location and routing for large-scale Peer-to-Peer systems[C].In Proc.of IFIP/ACM Middleware,2001.

[13]Ratnasamy S,Francis P,Handley M,et al.A Scalable content-addressable network[C]//In Proc.of ACM SIGCOMM,2001.

[14]Malkhi D,Naor M，Ratajczak D.A scalable and dynamic look up network[C]//In 21st ACM Symposium on Principles of Distributed Computing （PODC）.Monterey,CA,USA,2002.

[15]Kaashoek F,Karger D R.A simple degree-optimal hash table[C]//In 2nd international workshop on peer-to-Peer systems（IPTPS）.Berkeley,CA,USA,2003.

[16]Shen H，Xu C,Chen G.A constant-degree and lookup-efficient P2P overlay network[C]//In IPDPS,2004.

[17]Erd＂os P，R′enyi A.On random graphs[J].Publ.Math.Debrecen,1959（6）：290-295.

[18]Erd＂os P，R′enyi.A On the evolution of random graphs[J].Magyar Tud.Akad.Mat.Kutat′oInt.K′ozl,1960（5）：17-23.

[19]Vázquez A,Pastor-Satorras R,et al.Large-scale topological and dynamical properties of the Internet[J].Phys Rev E,2002（65）：066130-066135.

[20]Wang X，Chen G.Complex networks.small-world,scale-free,and beyond[J].IEEE Circuits and Systems Magazine,2003,3（2）：6-12.

[21]Chen G,Fan Z,Li Xiang.Modeling the complex Internet topology[C]//Complex Dynamics in Communication Networks.Springer Publisher,2004.

[22]Wang X,Chen G.Synchronization in scale-free dynamical networks:robustness and fragility[J].IEEE Transactions on Circuits and Systems,Part I:Regular Paper,2002,49（1）：54-61.

[23]Li Xiang,Chen Guan-rong.A local-world evolving network model[J].Physical A,2003,328（1/2）：274-279.