直流锅炉-汽轮发电机组的自适应PID控制①

王印松，岑 炜，李涛永，刘鸿达

(1.华北电力大学控制科学与工程学院，保定 071003;2.中国电力科学研究院，北京 100192;3.中石油华北油田采油三厂，河间 062450)

PID控制器是广泛应用于工业过程的控制策略之一。它具有结构简单、参数物理意义清晰等优点。在PID控制器的应用中，关键问题是如何在线或离线整定PID控制器的参数。传统的方法是在获取对象的数学模型基础上，根据某一整定原则来确定PID控制器参数。然而，火力发电机组往往具有非线性、时变、不确定性等特点，难以建立其精确的数学模型。这就要求在控制系统运行中，PID控制器参数变化不能依赖于对象原始数学模型，而需要根据具体运行工况在线调整，以达到满意的控制效果。针对上述问题，Wellstead等[1]提出了极点配置自适应控制算法，而后Wittenmark等[2]对该控制算法进行了相应的改进，Tjokro等[3]针对具有未知或时变纯滞后时间和可测量噪声干扰的控制系统，提出了极点配置自适应PID控制算法;文献[4～6]分别针对多功能除湿机的温度控制系统、电阻加热炉温控系统、同步发电机励磁控制系统研究了极点配置自校正PID控制器，均取得了比较满意的控制效果。

虽然，极点配置自适应PID控制算法已经比较成熟，也在工业过程控制中得到了广泛应用;但是，针对火电厂直流锅炉-汽轮发电机组中的锅炉-汽轮机协调控制问题，鲜见研究报道。本文针对某765 MW直流锅炉-汽轮发电机组在正常运行工况下的模型，研究了极点配置自适应PID控制算法。协调控制系统是一个非线性、大惯性、强耦合的动态系统，传统的PID控制很难取得满意的控制效果。为了解决这个问题，本文针对协调系统模型进行了双重动态解耦，然后在此基础上研究了极点配置自适应PID控制算法。仿真结果表明该控制策略能克服非线性、强耦合等干扰因素的影响，得到较理想的控制效果，是一种实际工程中可行且实用的控制策略。

1 直流锅炉-汽轮发电机组模型

文献[7]给出了某765 MW燃煤-燃气联合循环火力发电机组模型，其包含一台652.5 MW燃煤直流锅炉汽轮发电机组和一台112.5 MW燃气发电机组。燃煤蒸汽机组的直流锅炉有32个燃烧器，分四层布置;煤粉和空气经燃烧器送入炉膛后，在炉膛中呈切圆式燃烧;主蒸汽压力为19.5 MPa，主蒸汽温度为535℃。燃气轮机的排气流量大约为499 kg/s，温度大约为566℃，其送入蒸汽锅炉的炉膛用于加热和携带氧气，对燃煤蒸汽机组锅炉-汽轮发电机协调控制系统[7～9]的影响可以忽略不计。整个机组的原理如图1所示。其中:Y1、Y2为输出的电功率(MW)和锅炉焓值(J/g);U1、U2为输入的给煤量(kg/s)和给水量(kg/s)。

从控制工程角度而言，大型的火力发电机组的是一个时变、非线性、多变量耦合系统，是一个比较复杂的控制系统。一般来说，一台火力发电机组的输入变量包括:燃料、给水、减温水和助燃空气，输出变量包括:电功率、锅炉蒸发器出口焓值(为蒸汽温度和压力的函数)、排气等。由于燃气轮机组的动态系统相对比较简单，且对燃煤机组中的锅炉-汽轮发电机的协调控制问题影响较小，为了简化问题的分析，本文在研究燃煤机组直流锅炉-汽轮发电机协调控制问题时，忽略燃气机组的影响;建立一个以燃料量和给水量为输入量，蒸汽轮机输出的电功率和锅炉蒸发器出口焓值为输出量的动态系统模型，如图1所示。

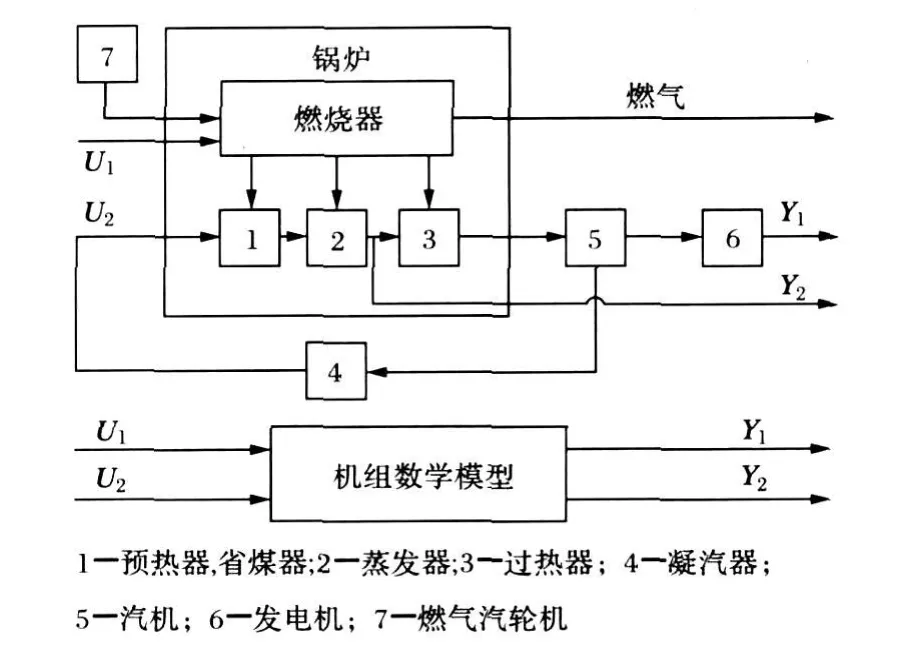
图1 直流锅炉机组协调控制系统模型原理Fig.1 Schematic diagram of the once-through boiler unit coordinating control system

在图1所示的模型结构中，燃料量和给水量作为输入变量，蒸汽轮机输出的电功率和蒸汽焓值作为输出变量。直流锅炉没有汽包，锅炉蓄热小，锅炉的蓄热对汽轮机输出的电功率的影响可以忽略。这样，在机组负荷波动过程中，蒸汽轮机输出的电功率的变化速度主要依赖于蒸发器产生蒸汽的速度。控制系统结构如图2所示。整个控制系统由控制器、解耦器和协调系统动态模型组成，两个控制器采用极点配置自适应PID控制器。

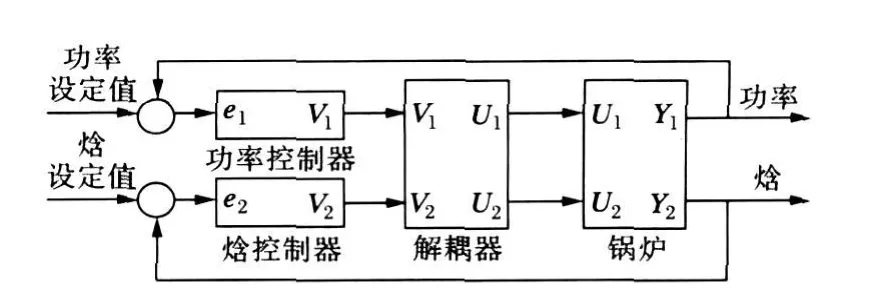
图2 火力发电机组控制系统结构Fig.2 Control system structure of the turbogenerator unit

蒸汽轮发电机组协调控制系统模型[7]为

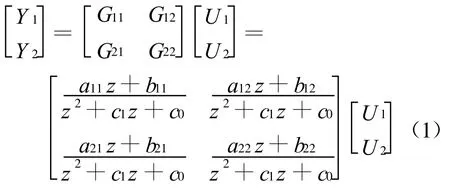
2 直流锅炉-汽轮发电机组极点配置自适应PID控制算法

自适应PID控制器的设计思想是:在模型参数估计和双重动态解耦的基础上，根据工程设计要求确定所期望的闭环系统极点分布，来自动调节PID控制器参数使闭环传递函数的极点位于理想的位置。极点配置自适应PID控制系统包含六个部分，PID调节器、初始模型解耦器、被控对象、最小二乘递推参数估计器、辨识模型解耦器、参数更新律，结构如图3所示。

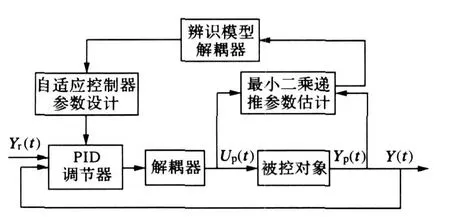
图3 自适应PID控制系统结构Fig.3 Structure diagram of adaptive PID control system

2.1 极点配置自适应控制律

考虑到过程扰动的影响，被控对象可表示为

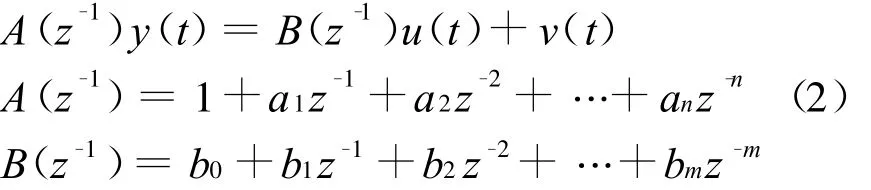
式中:u(t)为控制变量;y(t)为实测输出变量;v(t)为扰动;A(z-1)和B(z-1)为平移算子多项式。为简单起见，在以后的叙述中，直接用A和B表示。

设期望的闭环系统特性由传递函数表示为

式中，Am(z-1)和Bm(z-1)为互质多项式。为了达到期望的动态特性，可采用图4所示的控制方案[10]。

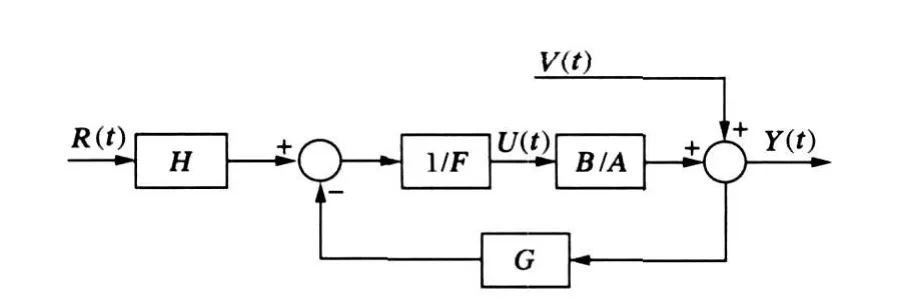
图4 极点配置自适应控制方案Fig.4 Pole placement adaptive control scheme

这样，反馈控制策略为

从式(2)和式(4)中消去 u，可得

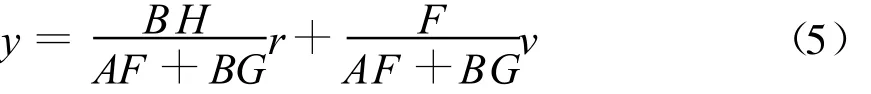
为了获得期望的动态特性

条件必须成立。

上式中的分母 AF+BG是闭环特征多项式。令T表示附加的观测器动态特性。于是得到Diophantine方程为

通过求解上述Diophantine方程可得出极点配置控制器参数。

2.2 动态解耦

对式(1)所描述的协调系统动态模型，为了建立自适应控制器的输出V1、V2和动态系统的输出Y1、Y2的一一对应关系，设计解耦器为

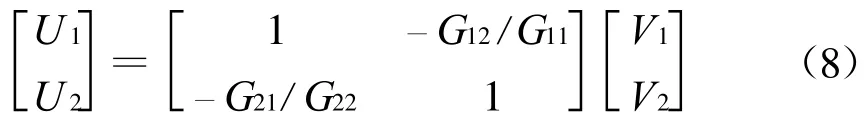
将式(8)代入式(1)得

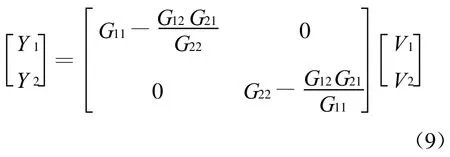
由此可知，Y1只依赖于V1，Y2只依赖于V2;这样动态系统就被解耦成两个单回路系统，控制器的设计就相对简单了。

2.3 极点配置自适应PID控制算法

解耦后的两个单回路系统的被控对象模型可分别描述为

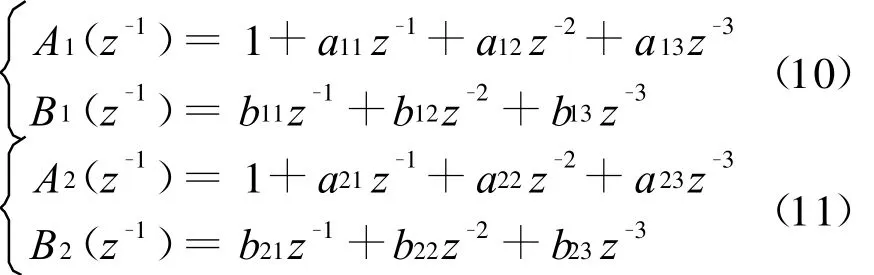
由于上述两个单回路多项式形式相同，可统一描述为

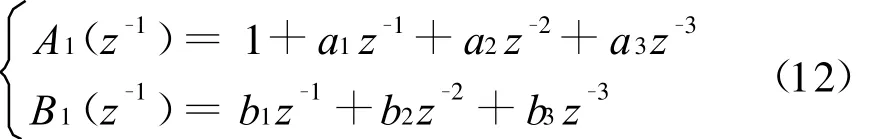
根据前面叙述的极点配置自适应控制算法取

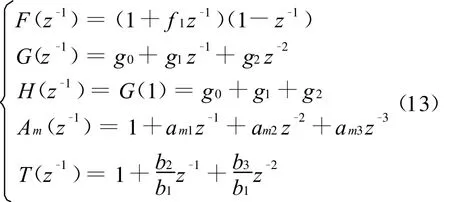
将式(13)带入式(7)可得

根据式(14)，计算 f1、g0、g1、g2的值 。

在数字控制系统中，通常采用带数字滤波器的PID控制器，控制算法[11]表示为

其中

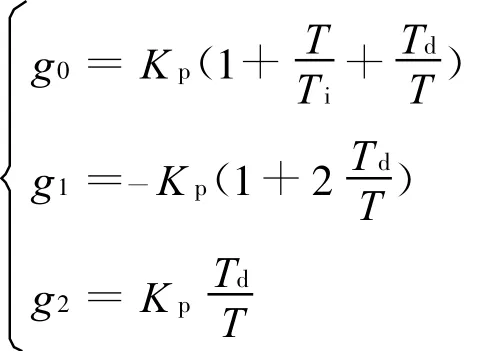
上一方程式对Kp、Ti、Td有唯一解，即

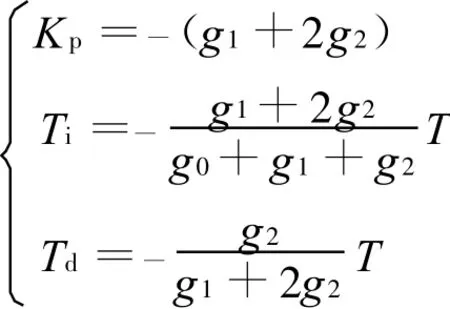
这样，就实现了自适应PID控制算法。

2.4 实时参数估计算法的改进

式(1)中的 aij(i=1 ，2;j=1，2)，ck(k=1 ，0)，bij(i=1，2;j=1，2)均为未知参数 ，在参数的在线辨识中，为了克服"数据饱和"现象，采用带遗忘因子的渐消记忆递推最小二乘算法分别辨识式(1)中各个传递函数中的系数。辨识算法如下。

其中，未知量参数向量θ为

数据量信息向量为

该递推算法表达式为

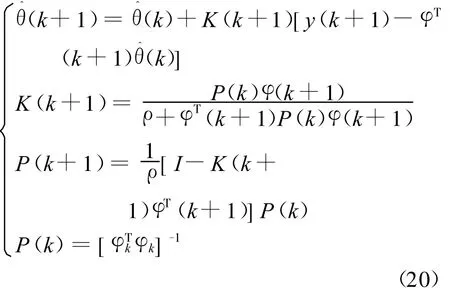
其中，ρ为遗忘因子。它的大小应根据参数的时变性由经验确定，一般范围为0.95～0.99[12];参数变化快时取值低，变化慢时取值高。

由于遗忘因子的存在，对于时不变系统或慢时变系统来说，经多次迭代后，遗忘因子的作用已把比较陈旧的数据赋予很小的权值，减小了历史数据的作用，加强了当前数据在模型辨识中的作用。

3 仿真研究

为了验证上述自适应PID控制器的有效性，下面通过2个仿真实验将它与传统PID控制器进行仿真对比。仿真实验中采用式(1)给出的蒸汽轮发电机组协调控制系统模型，该模型在95%工况下的传递函数为

3.1 设定值跟踪实验

在图2所示的控制系统中，对电功率和蒸汽焓值的设定值分别加一个幅值为0.5的阶跃信号。待控制系统输出稳定后，再加入幅值为-0.5的阶跃信号，仿真时间取为8 000 s。蒸汽轮机输出的电功率及锅炉蒸汽的焓值跟踪响应曲线如图5和图6所示。

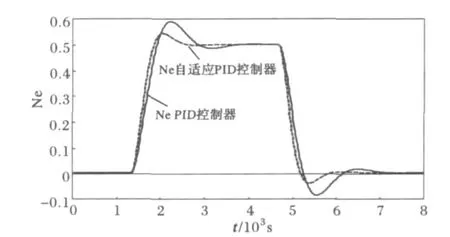
图5 输出功率对设定值阶跃扰动的跟踪曲线Fig.5 Tracking curves of output electric power follwing reference value step disturbance

图6 焓值设定值阶跃扰动跟踪曲线Fig.6 Tracking curves of boiler output enthalpy following reference value step disturbance

由图5和图6可以看出，在电功率设定值阶跃扰动下自适应PID控制系统能快速恢复稳定，且其超调量相对较小。极点配置自适应PID控制器的超调量大约是传统PID控制器的1/3，调节时间大约是传统PID控制器的1/2。在焓值跟踪实验中，自适应 PID控制器的焓值输出超调量大约是传统PID控制器的2/5，其调节时间大致是传统PID控制器的1/2。

3.2 脉冲扰动试验

在图2所示的控制系统中，在电功率和焓值控制器的输出端分别加入幅值为0.05、宽度为2 s的脉冲扰动;待控制系统稳定后，再加入幅值为-0.05、宽度为 2 s的脉冲扰动，仿真时间取为8 000 s。蒸汽轮机输出的电功率及锅炉蒸汽的焓值调节响应曲线如图7和图8所示。

由图7和图8可以看出，在脉冲扰动下，极点配置自适应PID控制器较传统PID控制器的调节速度较快，调节时间较短，且其波动也相对比较小。

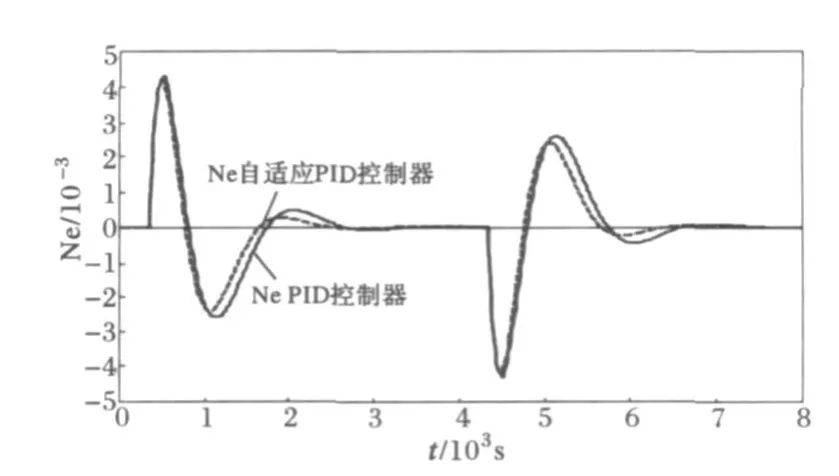
图7 电功率脉冲响应曲线Fig.7 Response curves of electric power following pules disturbance

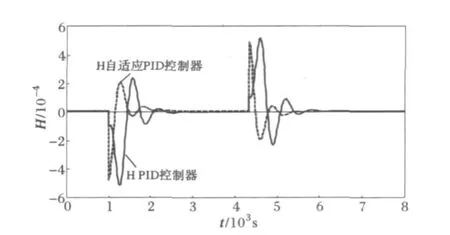
图8 焓值脉冲响应曲线Fig.8 Response curves of enthalpy following pulse disturbance

5 结语

本文针对直流锅炉-汽轮发电机组协调控制系统的动态模型设计了极点配置自适应PID控制算法。该算法不需要事先知道系统的精确模型，在线计算量小;能够在线辨识动态系统的模型，并进行动态解耦、自动更新PID控制器的参数。仿真实验表明本文所提方法具有较好的跟踪能力和自适应调节能力;与传统PID控制器相比，极点配置自适应PID控制器的超调较小，调节时间较短(电功率输出超调量大致是传统PID控制器的1/3，其调节时间大致是传统PID控制器的1/2;焓值输出超调量大致是传统PID控制器的2/5，其调节时间大致是传统PID控制器的1/2)，可以较好地解决火力发电机组锅炉-汽轮机协调系统的控制问题。

[1] Wellstead P E，Edmunds J M，Prager D，et al.Selftuning pole/zero assignment regulators[J].International Journal of Control，1979，30(1):1-26.

[2] Wittenmark B，Astrom K J.Methods and applications in adaptive control[J].Automatica，1991，27(6):21-30.

[3] Tjokro Supardi，Shah Sirish L.Adaptive PID control[C]∥American Control Conference，Boston，USA:1985.

[4] 李开霞，张金波，曹爱华(Li Kaixia，Zhang Jinbo，Cao Aihua).一种实用的自校正PID控制器设计与仿真研究(Design and simulation of an useful self-tuning PID controller)[J].计算机仿真(Computer Simulation)，2008，25(9):167-170.

[5] 刘伯春，殷建宁(Liu Bochun，Yin Jianning).极点配置自校正PID调节器及其应用(Pole assignment selftuning PID regulator and its application)[J].基础自动化(Basic Automation)，1995，36(4):9-12.

[6] 周双喜，张恒(Zhou Shuangxi，Zhang Heng).一种新型自校正 PID励磁调节器的研究(Self tuning PID excitation regulator for synchronous generators)[J].清华大学学报:自然科学版(Journal of Tsinghua U-niversity:Science and Technology)，1997，37(1):31-34.

[7] Kocaarslan Ilhan，Cam Ertugrul，Tiryaki Hasan.A fuzzy logic controller application for thermal power plants[J].EnergyConversion and Management，2006，47(4):442-458.

[8] Kocaarslan I，Cam E.Experimental modeling and simulation with adaptive control of power plant[J].Energy Conversion and M anagement，2007，48(3):787-796.

[9] Kocaarslan I.Application of adaptive control concept in a 750M W coal fired power plant[J].Control Engineering Practice，1994，2(6):711-718.

[10] 韩曾晋.自适应控制[M].北京:清华大学出版社，1995.

[11] 陶永红.新型PID控制及其应用[M].北京:机械工业出版社，1998.

[12] 李鹏波.系统辨识基础[M].北京:中国水利水电出版社，2006.

[13]田浩(Tian Hao).MATLAB在电机教学中的应用(Applications of M ATLAB in the teaching of electric machinery)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA)，2006，18(2):108-112.