具有网络诱导时延的非线性奇异网络系统脉冲控制器设计

赵贤林 费树岷 林金星

(1南京农业大学工学院，南京 210031)

(2东南大学自动化学院，南京 210096)

(3南京邮电大学自动化学院，南京 210003)

近年来，由于奇异系统在复杂电路、机器人、飞机模型、生物和混合经济等系统中具有十分广泛的应用，并且奇异系统在很多情况下表现出脉冲行为［1-2］，因此研究奇异脉冲控制系统有很重要的实际意义.对于脉冲系统的研究已取得一些成果.如文献［3］提出了脉冲控制和非线性脉冲控制系统的渐近稳定条件的概念.文献［4］通过使用一个新的比较定理给出了一类不确定系统的渐近稳定性条件.文献［5］用切换控制方法研究了奇异脉冲系统的稳定性、鲁棒镇定和H∞控制问题.文献［6-7］分别用线性近似法和LMI方法研究了系统稳定性问题.其他脉冲时滞系统，可以参考文献［8-11］及相关文献.而对网络控制系统的研究，文献［12-13］给出了具有网络诱导延迟和数据包丢失的网络控制系统的结论.文献［2］讨论了网络脉冲控制系统(NICS)的稳定性问题，文献［14］基于模型方法研究了具有传输时滞的网络脉冲控制问题.

另一方面，对于奇异非线性脉冲网络控制系统(SNICS)的稳定性分析以及控制器的设计，到目前为止，很少有文献涉及.因此，基于以上原因，本文主要讨论了具有传输延迟的非线性奇异网络脉冲控制系统(NSINCS)的稳定性问题.在文献［2］的基础上，本文给出了确定性和不确定性的奇异非线性脉冲网络控制器的设计方法.该网络控制器可以通过求解几个矩阵不等式得到.仿真结果表明了提出的方法是有效的.

1 问题的提出

非线性奇异网络脉冲控制系统模型可以描述为

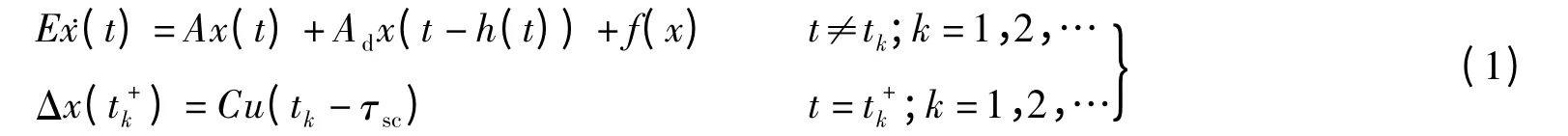
式中，x(t)∈Rn，u(tk)∈Rm分别为系统的状态变量和控制变量;h(t)≤T为时变时滞.其中，T是传感器的采样周期，E∈Rn×n形如并且0＜rank E=r≤n;A，Ad，C是具有适当维数的常数矩阵;对于t≥t0存在正数L，使得对所有x(t)∈Rn满足‖f(x(t)‖≤L‖x(t)‖;0≤τsc≤tk－tk－1指从传感器到控制器的网络传输延时;x(t1－τsc)=φ(t)为系统的初始值，脉冲间隔}满足)，并且

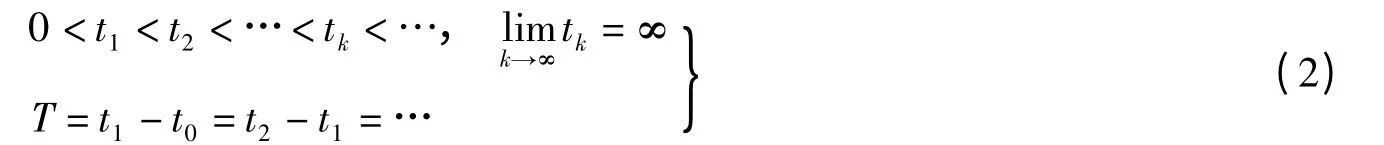
对于不确定的非线性奇异网络脉冲控制系统，模型可以描述如下:

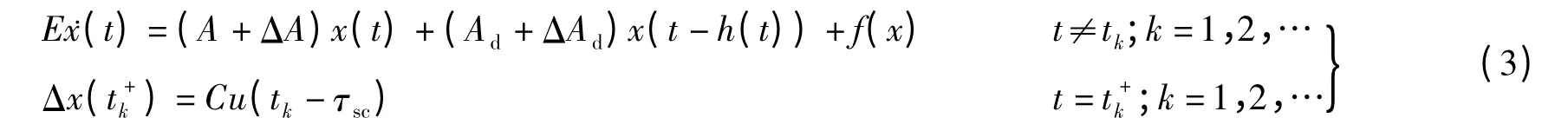
式中，ΔA，ΔAd为容许的不确定参数，满足[ ΔA ΔAd]=MF(t)[ G1G2]，M，G1，G2为适当维数的常数矩阵，F(t)是未知Lebesgue可测函数，满足FT(t)F(t)≤I.

定义1 当det(sE－A)≠0，则称矩阵对(E，A)是正则的;并且当rank(sE－A)=rank E，则(E，A)是自由脉冲.

定义2 若存在常数a＞0，b＞0，则当t＞t0时，如果有‖Ex(t)‖≤a‖Ex(t0)‖e－b(t－t0)，则称系统(1)和(3)是E指数稳定的.

假设1 ①矩阵对(E，A)是正则的，即det(sE－A)≠0;②信号传输中无数据包丢失.

引理1［14］如果矩阵对(E，A)是正则的和自由脉冲，则对于相应的初始条件φ(t)∈Cn，τ，系统(1)和(3)在［0，+∞)存在一致连续解.

引理2［3］系统(1)和(3)的E指数稳定等价于指数稳定.

引理3 设V(t)是一个正定的标量函数，并满足下列条件:

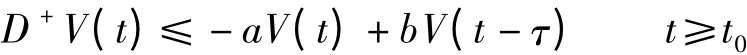
式中，a，b为大于0的常数.则当t≥t0时，存在一个正数α，使得下式成立:

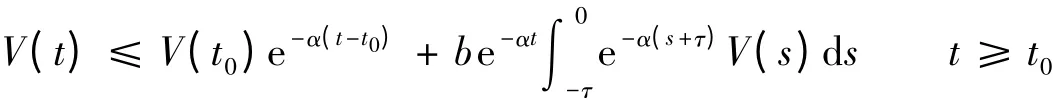
式中，α满足α－a+b eατ0=0.

2 不确定非线性奇异网络系统脉冲控制器设计

对于不确定非线性奇异网络系统(3)，有以下定理:

定理1 如果存在矩阵P，K及常数ε＞0，其中P可逆，有以下条件成立:

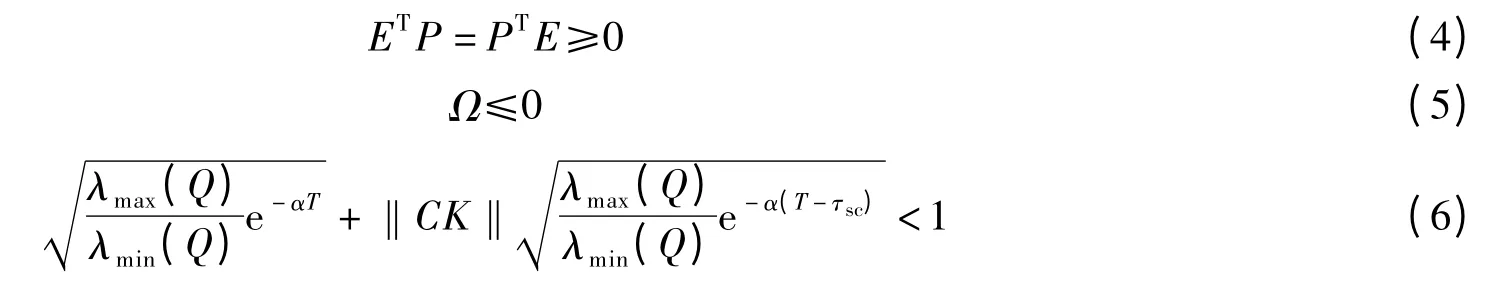
式中，a＞b＞0，正定对称矩阵Q满足ETP=ETQE.

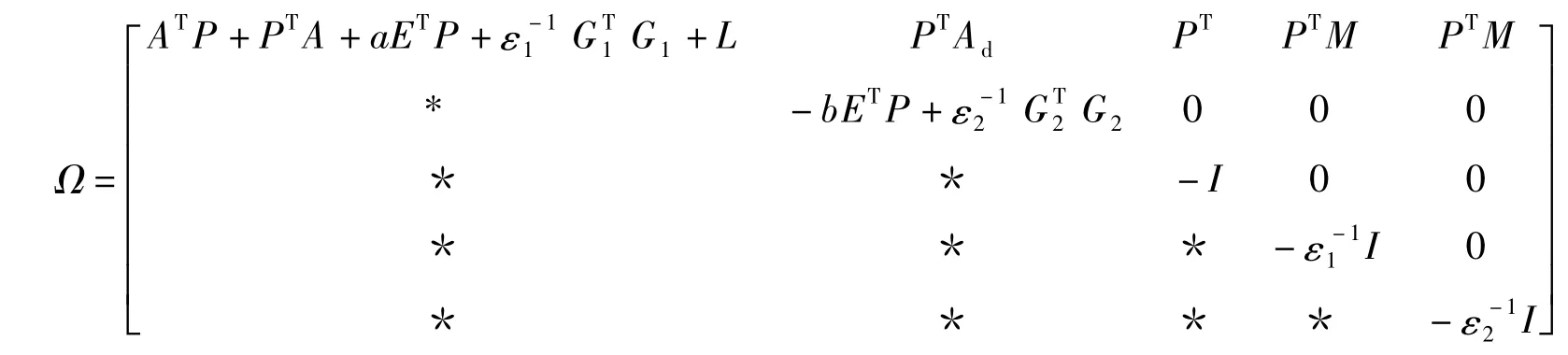
式中，α＞0满足为方程α－a+b eατ0=0的解.则系统(3)在控制器u(tk－τsc)=Kx(tk－τsc)作用下是指数稳定的.

证明 考虑Lyapunov函数为V(t)=xT(t)ETPx(t)，则当t∈(tk－1tk］时有

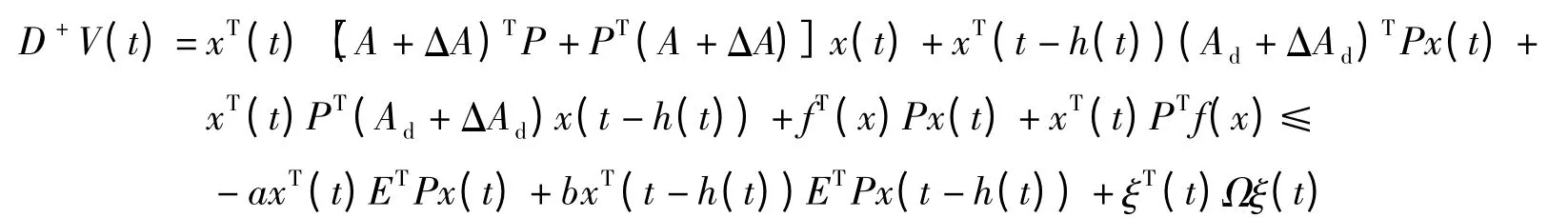
式中，ξT(t)=[xT(t)xT(t－h(t))]T.因此，当条件(5)成立时，由引理3知，对于t∈(tk－1tk］有V(t)

由于ETP=PTE=ETQE≥0，并且P为可逆的，因此有下式成立:

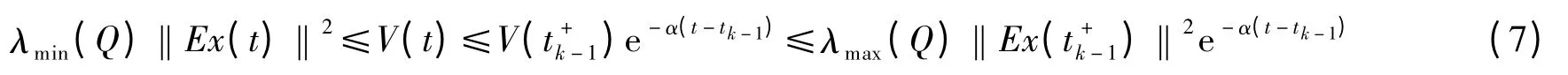
由引理2知，条件(4)、(5)成立时，系统(3)在t∈(tk－1tk］时是指数稳定的.

另一方面，当t=t+k时，

因此有

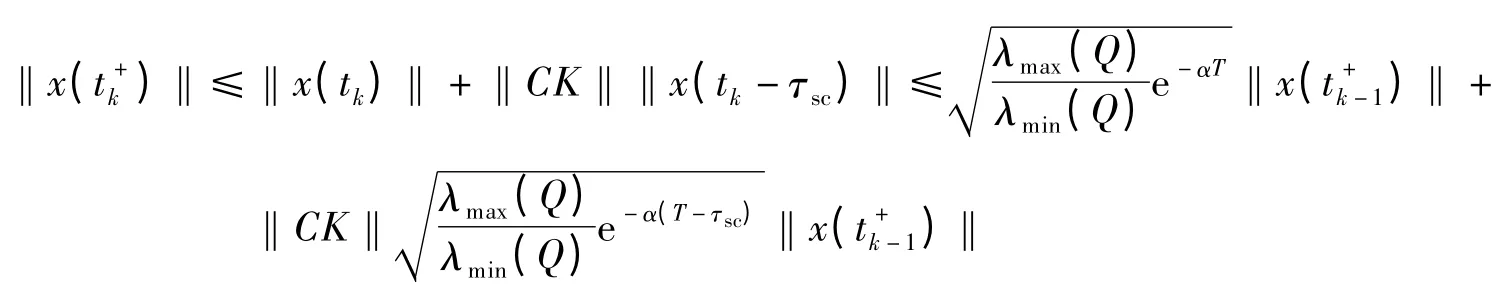
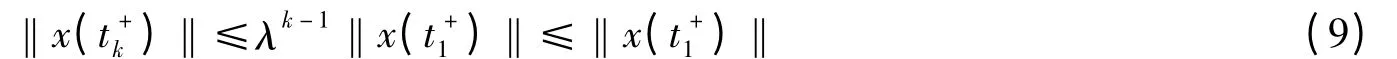
所以有V(t)≤e－α(t－t1)V(t+1).故当条件(6)成立时，系统(3)在时刻t=t+k是指数稳定的.

综上所述，当条件(4)～(6)成立时，系统(3)在控制器u(tk－τsc)=Kx(tk－τsc)作用下在t∈内是指数稳定的.证毕.

对于非线性不确定奇异网络控制系统(3)，当ΔA=ΔAd=0时，系统(3)退化为系统(1).令定理1中M=G1=G2=0，则有以下推论成立:

推论1 如果存在矩阵P，K及常数ε＞0，其中P可逆，有以下条件成立:

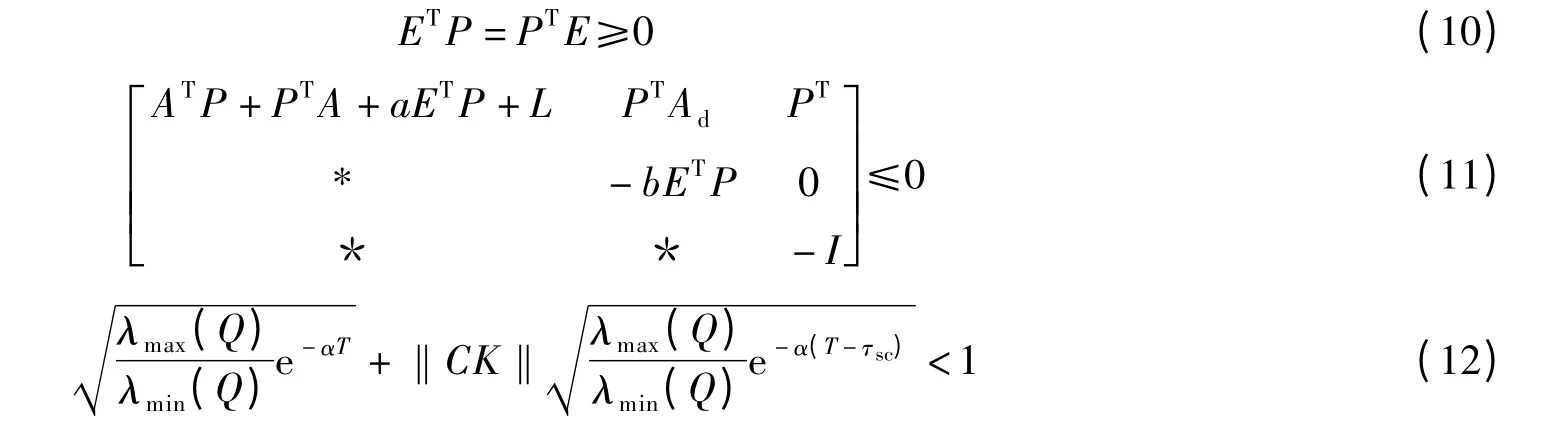
式中，a＞b＞0，正定对称矩阵Q满足ETP=ETQE，α＞0满足为方程α－a+b eατ0=0的解.则系统(1)在控制器u(tk－τsc)=Kx(tk－τsc)作用下是指数稳定的.

3 仿真算例

考虑如下系统(3)，参数分别为

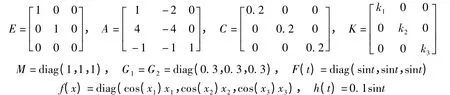
本文取τsc=0.05;tk－tk－1=0.1;a=3;b=2.根据定理1，得到，α=0.292;并且‖I+CK‖≤0.8203，因此取k1=k2=k3=－1.75.系统的初始条件为φ(t)= [ 1 2 3]时，仿真曲线如图1所示.

从图1中可以看出，当非线性奇异网络系统(3)满足定理1的3个条件时，则该系统在脉冲时滞控制器u(tk－τsc)=－1.75x(tk－τsc)作用下是指数稳定的.

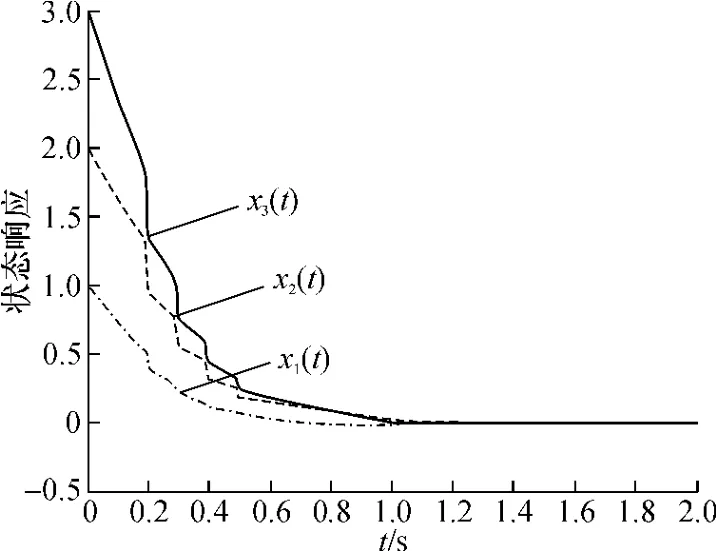
图1 系统状态响应曲线

4 结语

本文主要研究了具有诱导网络时滞的确定性和不确定非线性SNICSs的控制器设计问题.根据Lyapunov函数理论，通过求解一组线性矩阵不等式得到正定矩阵P，通过求解不等式得到相应的脉冲时滞控制器增益K.利用本文的脉冲控制器设计方法，可以使得闭环系统在容许的不确定范围内达到指数稳定.数值仿真算例体现了所用方法的有效性.

References)

［1］Suykens J A K，Yang Tao，Vandewalle JL O.Impulsive control and synchronization of chaos［M］//Chen G.Controlling Chaos and Bifurcations in Engineering Systems.Boca Raton，FL，USA:CRC Press，1999:275-298.

［2］Guan Zhihong，Huang Jian，Chen Guanrong.Stability analysis of networked impulsive control systems［C］//Proceedings of the 25th Chinese Control Conference.Harbin，China，2006:2041-2044.

［3］Yao Jing，Guan Zhihong，Chen Guanrong.Stability，robust stabilization and control of singular-impulsive systems via switching control［J］.Systems and Control Letters，2006，55(11):879-886.

［4］Yang Tao.Impulsive control［J］.IEEE Trans Auto Control，1999，44(5):1081-1083.

［5］Sun Jitao，Zhang Yinping，Wu Qidi，Less conservative conditions for asymptotic stability of impulsive control systems［J］.IEEE Trans Automatic Control，2003，48(5):829-831.

［6］Ye Hui，Michel A N，Ling Hou.Stability theory for hybrid dynamic systems［J］.IEEE Trans Automatic Control，1998，43(4):461-474.

［7］Ding X J，Xu Honglei.Robust stability and stabilization of a class of impulsive switched systems［J］.Dynamics of Continuous Discrete and Impulsive Systems:Series B，Applications and Algorithms，2005，SI2(6):795-798.

［8］Yan Jurang，Shen Jianhua.Impulsive stabilization of functional differential equations by Lyapunov-Razumikhin functions［J］.Nonlinear Anal Theory，Methods Appl，1999，37(2):245-255.

［9］Liu Xinzhi.Stability of impulsive control systems with time delay［J］.Math Comput Model，2004，39(4):511-519.

［10］Li Chuandong，Liao Xiaofeng，Zhang Rong.A united approach for impulsive lag synchronization of chaotic systems with time delay［J］.Chaos Solitons Fractals，2005，23(1):1177-1184.

［11］Yang Zhichun，Xu Daoyi.Stability analysis and design of impulsive control systems with time delay［J］.IEEE Trans Automatic Control，2007，52(8):1448-1454.

［12］Fridman E.Stability of linear descriptor systems with delay:a Lyapunov-based approach［J］.Math Anal Appl，2002，273(1):24-44.

［13］Zhu Shuqian，Zhang Chenghui.Delay-dependent robust stability criteria for two classes of uncertain singular time-delay systems［J］.IEEE Trans Automatic Control，2007，52(5):880-885.

［14］Zhang Wei，Branicky M S，Phillips S M.Stability of networked control systems［J］.IEEE Control Syst Mag，2001，19(2):84-99.