一种改进的七电平逆变器对比仿真研究
孙长冬 黄松清 刘绪良 谢玉干 龙佼佼
(安徽工业大学电气信息学院,安徽 马鞍山 243002)
1 引言
近年来,多电平结构大量应用于高压大功率等场合,主要是多电平逆变器由于其电平数多、开关频率低、输出谐波小等特点,因此越来越受到重视,并得到迅速发展。到目前为止,各国学者提出了大量的拓扑结构,归纳起来主要有三种:二极管钳位型、飞跃电容型多电平逆变器、级联型。
传统的逆变器由于输出的PWM脉冲波电平数很少,因此存在很高的电压变化率和共模电压,而且波形谐波含量较大,使得输出滤波器的设计更加复杂。为了解决这些问题,发展了各种多电平逆变器电路。所谓多电平逆变器,就是采用多个直流电源和电力电子器件经过特定的拓扑变换,控制不同的直流电源输出,将其组合成不同幅值的多电平交流输出的功率变换装置。这种逆变器在高压大容量电力电子系统中发展迅速,成为电力电子领域新的研究热点。自1980年日本学者A.Nabse提出三电平中点钳位式逆变电路以来,经过多年的发展,现已形成钳位型和级联型两大类多种样式的多电平逆变器拓扑结构。丰富了多电平逆变电路的拓扑形式。
本文结合传统两电平逆变器和嵌位多电平逆变器的拓扑结构,取长补短,既采用了两电平电路结构,也吸取三电平钳位的优点,以及当今非对称电路拓扑的研究的特性,提出本文所研究的七电平逆变器的拓扑结构,并对分析了电路的工作原理,通过Matlab对其仿真,用简单的硬件电路验证了分析和仿真的正确。此电路和三电平逆变器的单相所用的开关管数量相当,钳位二极管减少,但是电平数增加到七电平。
2 电路拓扑
图1给出了单相7电平逆变器的电路拓扑和5电平电路拓扑,7电平电路也正是在5电平电路的基础之上,5电平工作过程见参考文献[1],结合钳位3电平逆变器,才产生的本文的研究电路拓扑,增加2个开关管,电平数也增加2个,控制方法大致相同。本文主要是对7电平逆变器进行分析和研究,左边的7电平电路拓扑的前边 Q3,Q4组成的桥是传统的2电平单相桥,后边的 Q5,Q6,Q7,Q8桥是钳位3电平的单向桥,用 Q1,Q2对电源进行控制,通过对此拓扑进行适当的控制,产生期望的7电平。主要是通过控制开关的导通,让电源叠加,产生7电平。7电平仅仅是将后板桥换成了钳位3电平的形式,可以再换成钳位5电平,可以产生11电平。依次类推可知,如果换成钳位七电平逆变器的半桥可以产生15电平。同样如果换成理想的钳位N电平逆变器,可以产生(2N+1)个电平。电平数越高,需要的独立电源也越多,控制也会变的更加复杂。

图1 5电平逆变器电路拓扑和改进的7电平电路拓扑
3 拓扑的工作原理
5电平逆变器的工作原理在此就不再分析,重点分析7电平逆变器的工作原理,图1有7种工作形式,本文主要对下面这7种工作状态进行了分析和研究。
(1)第1种工作状态,令Q3和Q6导通,其余的开关管关闭。电流从电源V2的正极开始,通过Q2的反并联二极管,以及Q3和Q6,还有嵌位二极管D2形成电流回路,最后流回电源V2的负极。输出电压为+V2。
(2)第2种工作状态,在Q3和Q6导通的基础上,再令Q8导通,从电源V2的正极开始,通过这三个开关管,流回V3的负极,逆变器输出电压为+(V2+V3)。
(3)第3种工作状态,在以上开关管导通的基础之上,再打开Q1,电流从电源V1的正极开始通过Q1,Q3,Q6,Q8流回电源V3的负极,逆变器输出电压为+(V1+V2+V3)。
(4)第4种工作状态,令Q2导通,其余的开关管都关闭,电流通过Q2,然后通过Q4,Q5,Q6的反并联二极管,形成续流回路,此时输出电压为0,还有其他的0导通状态,此处不再分析。
(5)第5种工作状态,令Q4,Q5导通,其它开关都关闭,电流从V3的正极开始,通过钳位二极管D1,以及Q4,Q5,最后流回V3的负极。逆变器输出电压为-V3。
(6)第6种工作状态,在第5种工作状态的基础之上,再令Q7导通,电流从V2正极开始,经过Q2的反并联二极管,再通过Q4,Q5,Q7流回电源V3的负极,逆变器输出电压为-(V2+V3)。
(7)第7种工作状态,令Q1,Q4,Q5,Q7导通,其余都关闭,电流从电源V1的正极流出,通过Q1,Q4,Q5,Q7后,流回 V3的负极,逆变器输出的电压为-(V1+V2+V3)。
(8)第8种工作状态,令Q2导通,其余开关管都关闭,形成电流的续流回路,逆变器输出的电压为0。
4 电路拓扑的控制原理
一种拓扑结构,必须采用合适的调制方法,才能得到期望的输出,不同主电路结构的逆变器都对应有一定的调制方法。本文采用SHEPWM,作为该拓扑的调制方式。该方式的思想是通过傅里叶级数分析,得出特定开关角下的傅里叶级数展开式,然后令某些特定的低次谐波为零,从而得到一个反映N个开关角的N个非线性独立方程,按求解的开关角进行控制,必定不含这些次数的谐波。通常这种方法着眼于低次谐波和低频次非3倍次谐波。假设V1= V2= V3=E,图2明显满足狄利克雷充分条件,又属于1/4周期对称的波形,所以傅里叶级数不存在余弦项和偶数谐波。于是可得
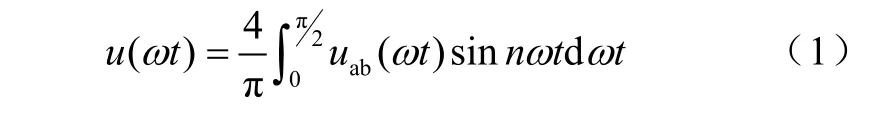
式中,uab是期望输出的相电压波形。
将式(1)展开,并解此积分,可得
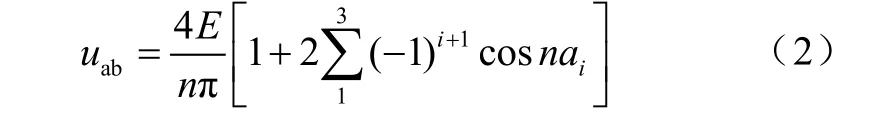
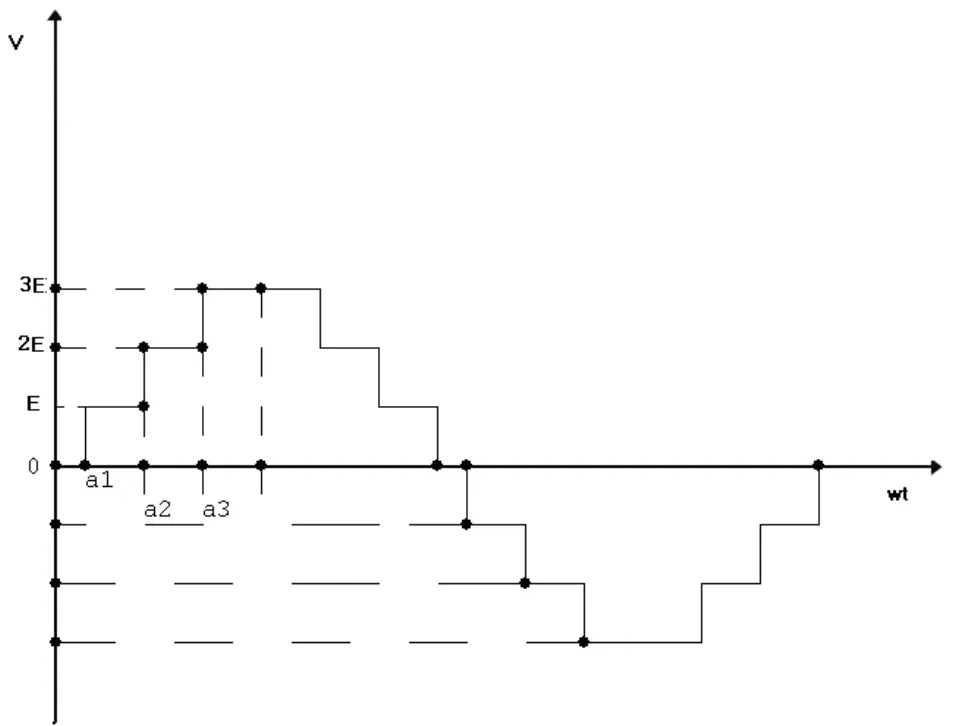
图2 逆变器输出电压波形
令u=(-1)i+1cosnai为调制比,其值的大小决定了直流电压利用率的大小。由式(2)可列出非线性方程为
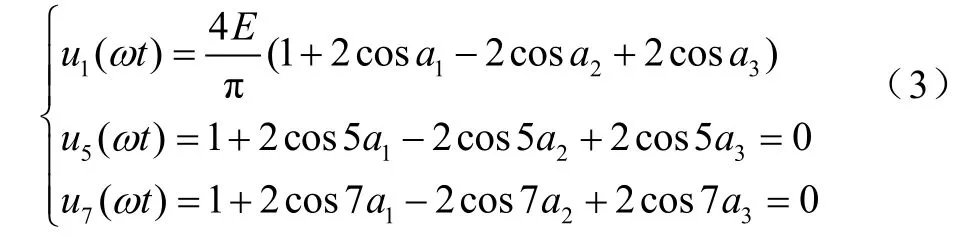
根据式(3),并利用牛顿迭代法,即可解出a1、a2、a3的值,从而实现电路的SHEPEM控制。现利用Matlab7.1中的相关数学工具,解出了不同调制比下a1、a2、a3的值。算出角度后,用一个常量代替角度值,与固定周期的正弦波相交,就可以产生相对应的驱动波形。
5 仿真结果
图3是通过Matlab6.5建立的系统仿真模型,a为5电平逆变器的仿真模型,b为7电平逆变器的仿真模型,每个直流电源的电压为100V,5电平逆变器的最大直流电压为400V而7电平逆变器的直流最大电压为300V,设置频率为50Hz,仿真结果如图4。取了前0.1s的输出波形。拓扑电路的驱动的搭建比较复杂,基本原理就是用正弦波和计算出来的具体角度值的差值,产生驱动。从输出的仿真实验结果可以看出,7电平逆变器的波形更加近似正弦波。能够按照预期的控制方法输出波形。
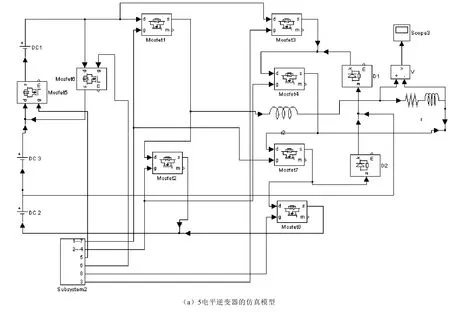
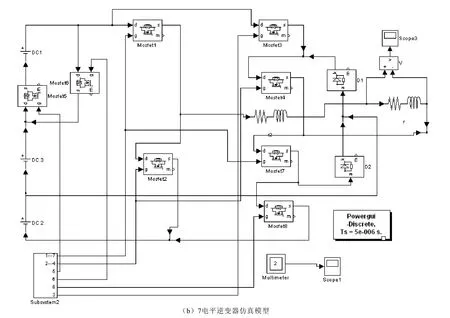
图3
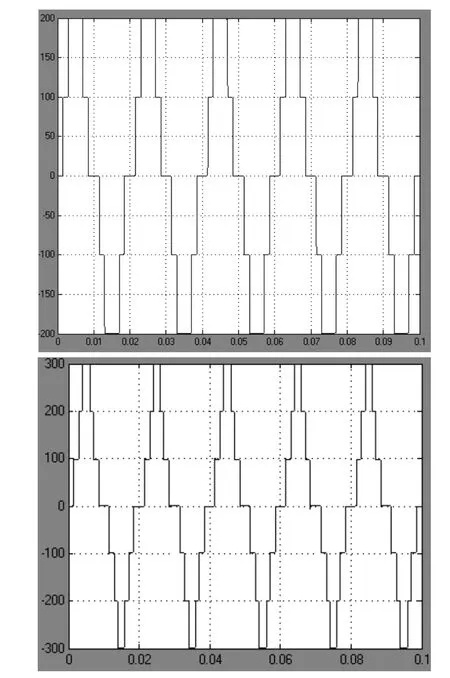
图4 逆变器输出电压波形
6 结论
改电路是对原有的五电平逆变器电路拓扑的改进,控制思路简单,产生的电平数高,通过了软件仿真设计和单相电路的研究,三相电路的控制还在进一步的研究,实验结果表明,这种电路能够在控制合理的条件下正常工作,且输出稳定。应用于大功率场合更能体现多电平的好处。
[1]MiroMilanovic,Franc Mihalic and Drago Dolinar.“Component Minimized Topology of DC to three-phase Inverter. World Scientific Publishing Company. 2004,13(4):863–875.
[2]李永东.大容量多电平逆变器-原理、控制、应用[M].北京:科技出版社, 2005.
[3]张艳莉,费万民.三电平逆变器SHEPWM 方法及其应用研究[J].电工技术学报,2004,19(1):17-19.
[4]王兆安,黄俊.电力电子技术(第4版) [M].北京:机械工业出版社,2006.
[5]洪乃刚.电力电子和电力拖动控制系统的MATLAB仿真[M].北京:机械工业出版社,2006.

