三相SPWM逆变电源输出电压的谐波抑制综合方法
王正 潘高强
(沈阳工业大学电气工程学院,沈阳 110178)
1 引言
随着SPWM控制技术在电力电子逆变电源的广泛应用,为了降低逆变电路输出侧产生的高次谐波对其负载和周围电气装置所产生的负面影响,人们把改善输出波形,消除谐波,提高波形质量作为一项重要的研究内容。所以,对SPWM波形的谐波分析有着十分重要的意义。
针对现代各行各业对电气设备控制性能日益提高的要求,本文对电压型SPWM逆变电源的控制方法进行了谐波分析,根据谐波在频谱上的分布情况,提出减少谐波对电机及其他用电设备危害的方法。
2 SPWM逆变电源模型的建立
正弦脉宽调制(Sinusoid Pulse Width Modulation-SPWM)是在脉宽调制(PWM)的基础上发展起来的。因其调制波采用正弦波故称为正弦脉宽调制。正弦波脉宽调制SPWM是利用三角波与正弦波的交点作为逆变电源的开关控制信号,SPWM逆变电源主电路和控制方式波形如图1所示。其中逆变电源的主回路采用高速开关元件,以保证逆变电源能工作在较高的开关频率下。SPWM控制技术的实质在于功率开关元件的开关信号是通过期望频率的正弦调制波与特定的载波信号相比较而获得的。这种方法适用于各种调频或调压装置中,是一种开关式稳压电源领域广泛应用的方法。在变频器中,通过正弦脉宽调制来控制逆变电源的功率开关器件的导通或关断,将整流器变换成的直流电压逆变为具有可控幅值和频率的电压源。
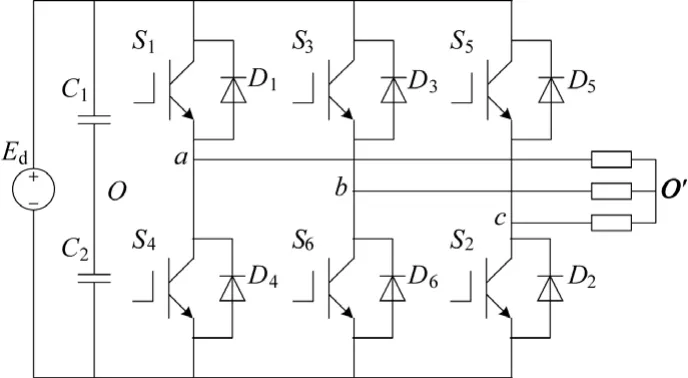
图1 三相SPWM逆变电源原理图
3 SPWM逆变电源的谐波分析
3.1 谐波分析的基本假设
为了便于分析谐波,在此对SPWM逆变电源作以下假设.
假设1:支流环节电压Ed是最理想的电压源,不考虑其纹波对逆变器输出的影响;
假设2:视功率开关元件为理想器件,具有理想的开关特性。
3.2 逆变电源输出电压的谐波分析[1]
在3.1的假设下,SPWM逆变电源的输出相电压傅里叶级数表示为
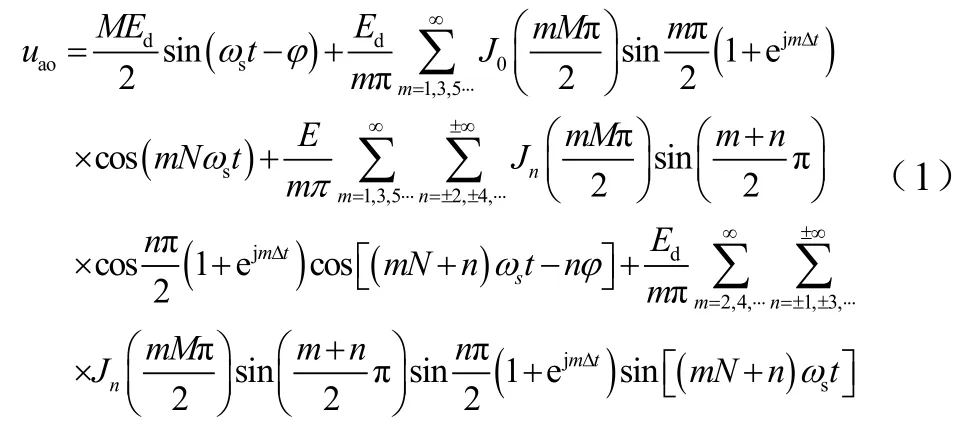
同理可得ubo、uco,所以在不考虑死区Δt的情况下,线电压uab=uao-ubo,将上式代入并简化得
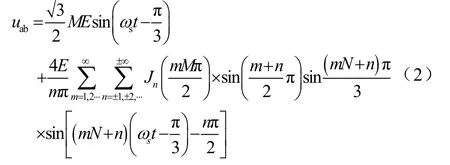
式中,ωs=2πfs;fs为调制波频率;Ed为直流电源电压;M为调制度;N为载波比;m为相对于载波的谐波次数;n为相对于调制波的谐波次数;φ为调制波初相; J0,⋅ ⋅⋅,Jn为第一类Bessel函数。
由式(2)输出电压的谐波集中分布在
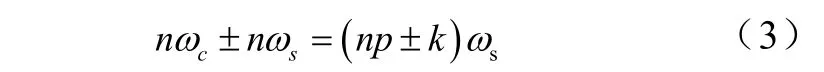
其中,n=1,3,5,…时,k=3(2m-1)±1,m=1,2,3…n=2,4,6…时,k=6m±1,m=0,1,2,…,或k=6m±1,m=0,1,2, …,
由上式可知,在载波频率的整数倍处的高次谐波不再存在。SPWM 的谐波分布带有明显的“集簇”特性,也就是一组一组地集中分布于载波频率的整数倍频率两侧,而且在每一组谐波中,随着k的增大,即远离该组谐波的中心,则谐波幅值通常逐渐减小。值得考虑的最低次谐波为p-2次。另外,由于3的整数倍次谐波属谐波分量,故逆变电源输出线电压中将不存在3的整数倍次谐波。
4 SPWM逆变电源的谐波抑制
为抑制SPWM电压源型逆变电源的输出谐波,从工程实际出发,正确选择和精确实现载波频率是使输出波形改善的最简洁途径。但是随着载波频率的提高,会增加功率元件的开关次数和开关损耗,提高对功率元件和控制电路的要求。本文将分别从调制法和计算法两个角度来提出SPWM逆变电源的谐波抑制方法。
4.1 基本的抑制方法[2]
选择合适的载波频率,以消除低次和某些奇次谐波。SPWM的载波频率越高,则逆变器输出电压谐波频率也就越高,所需的滤波器的体积就越小。虽然提高载波频率可以消除逆变器的低次谐波减小电机的谐波损耗,但是也会使逆变器开关损耗大幅度增加。因此为协调二者的矛盾,一般认为在中小功率的IGBT逆变器中,SPWM的载波频率取3kHz左右为宜。同时,载波比N应为3的整数倍,以消除3的整数倍数次谐波。
精确实现选定的载波频率,以避免异步调制中会出现的偶次谐波。但是,在实现选定的载波频率时,无论采用模拟电路,还是采用数字电路,总是不可避免地带来一定的误差。为避免以上情况的出现,需要设法使载波频率精确实现,尽可能减小载波频率误差。在载波频率误差不可避免的情况下,可在SPWM的实现中强行使载波和正弦调制波同步。
4.2 调制法
所谓调制法就是在正弦调制波中叠加入一定比例的零序谐波,即3倍频谐波的谐波注入式SPWM(HIPWM)。它能使调制波呈现出马鞍形,以降低调制波幅值,增大直流电源电压的利用率,同时又能使逆变电源具有良好的谐波抑制特性[1,3]。
在正弦函数中注入一定的零序谐波后,其调制函数可表示为
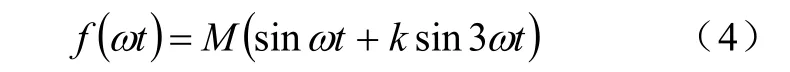
式中,Μ为调制系数;k∈[0,1]为注入的3次谐波的系数。
当k 取不同值时,调制函数 f(ωt )中注入的3次谐波含量亦不同。图2为调制系数Μ为0.9情况下k 不同时的调制函数波形,其中包括k=0、0.1、0.2、0.5四种情况。
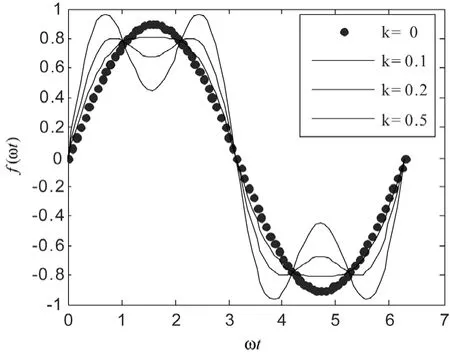
图2 注入三次谐波后的调制函数波形图
由图2可见,改变k便可改变调制函数 f(ωt)与横轴之间包围的面积,从而可使逆变器输出电压的幅值随之改变。同时,当逆变电源加入对称负载时,3的整数倍谐波自行消失,因此,注入3次谐波分量的SPWM并不增加逆变器输出电压中的谐波含量。
4.3 计算法
本文介绍在计算法中一种较有代表性的方法——特定谐波消去法。其基本理论是在电压波形的特定位置设置“缺口”,通过每半个周期间中逆变器的多次换向,恰当地控制逆变器脉宽调制电压的波形,通过脉宽平均法把逆变器输出的方波电压转换成等效的正弦波,以消除某些特定的谐波。
若以图1中的直流侧电压中点O为参考点,可得出a相双极性的电压输出波形,如图3所示。而b、c相的电压波形只需将a相的波形移相120°和240°即可得到[4-5]。

图3 特定谐波消除PWM的相电压波形
从0到π /2的电压波形有N个开关时刻,波形在[0,2π]域对 π 点为中心对称,在[0,2π ]域对 π/2点为轴对称,因此,a相电压的傅里叶级数为

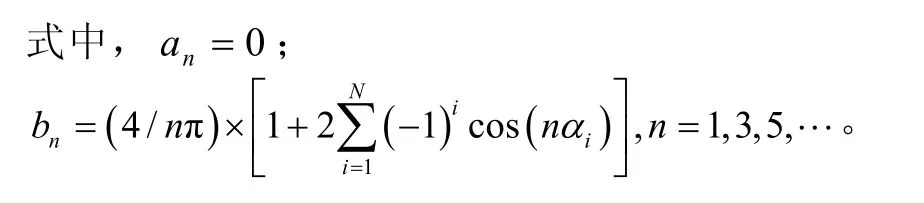
式(5)表明,谐波幅值与开关角α有关,只要适当选择N个α值,就可以使基波电压得到控制并且消除N-1个频率的特定谐波。对于三相对称负载而言,3的整数倍次谐波在线电压中因同相被抵消,所以只存在的谐波次数为5,7,11,13,…。
如果令q为选定的输出基波电压与逆变器直流侧电压的幅值比[(E1Ed2)],被指定消除的N-1个谐波幅值为零,则周期内的开关角的方程组为
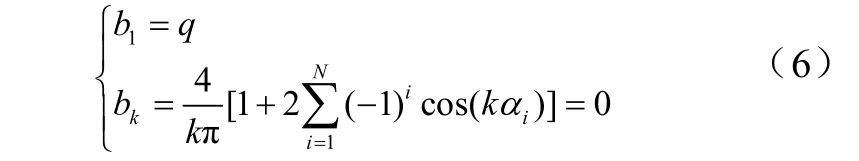
式中,k=6±1(i =1,2,⋅⋅⋅)为谐波次数;αi为1/4周期内第j个开关角。
5 仿真与试验验证
5.1 调制法的仿真验证
本文就图1所示电路应用Matlab/Simulink作仿真分析[6]。仿真负载为异步电动机,电动机星形连接,空载运行,逆变器采用双极性同步调制,载波为共用的等腰三角波,频率 fc=2850Hz;调制波为三相正弦波,频率 fs=50Hz,调制度M=0.9。式(4)中k从0到0.5之间变化,得出在不同3次谐波系数k时逆变器输出电压谐波含量变化如表1所示。

表1 不同k时逆变器输出线电压谐波含量变化
由表1可知,当k=0(即没有注入三次谐波)时,逆变电源输出线电压uab的THD为29.88%。
当k由零逐渐增大时,逆变电源输出线电压THD就逐渐减小。直到k=0.25时,逆变器输出线电压uab的THD为21.66%,此时逆变电源输出线电压uab的THD最小。
当k值超过0.25时,逆变器输出线电压uab的THD又逐渐增大。当k=0.5时,逆变器输出线电压uab的THD为28.56%。由以上分析说明:三次谐波分量的注入并不是越多越好,更不能随便定一个数值,而是要根据具体的电路结构和载波频率来选择一个比较合适的值。本文仿真得到比较理想的k值为0.25。
在某种意义上,可以认为注入3次谐波分量的SPWM逆变器输出电压中的谐波含量有所减小,从而在一定程度上改善了逆变器的输出电压特性。
5.2 计算法的仿真验证
同调制法的仿真一样,本文也利用Matlab对SHE做了仿真验证。负载为异步电动机,电动机星形连接,空载运行,N=9,fc= 2850Hz,fs= 50Hz,q=0.6,Ed2=190V;实验步骤包括:利用编制的开关角计算程序,计算出事先设定的q、N值所对应的开关角时刻并生成数据文件。将该数据文件与仿真实验模型相连,用于控制触发角。
据式(4)所抑制的谐波次数来看,对于给定的N,能抑制的最大谐波次数为。也就是说,谐波出现的次数应为以上的谐波。本文N=9时,能抑制的最大谐波次数为25,在频谱图上就会出现29次以上的谐波。表2为N=9时基波及各次谐波幅值,图4和图5为SPWM调制与SHEPWM调制线电压的频谱图。
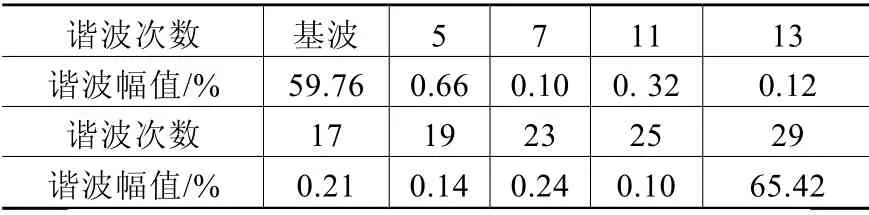
表2 基波及各次谐波幅值
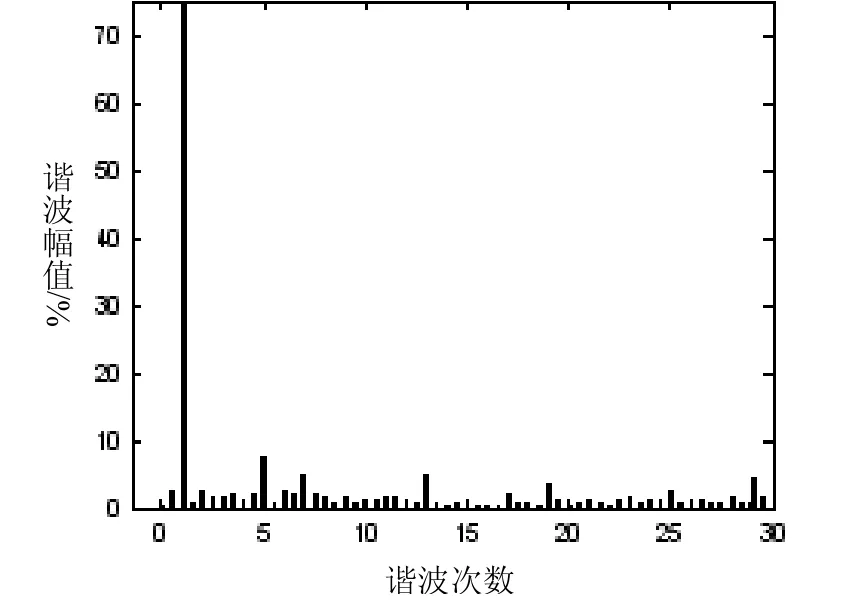
图4 SPWM线电压频谱图
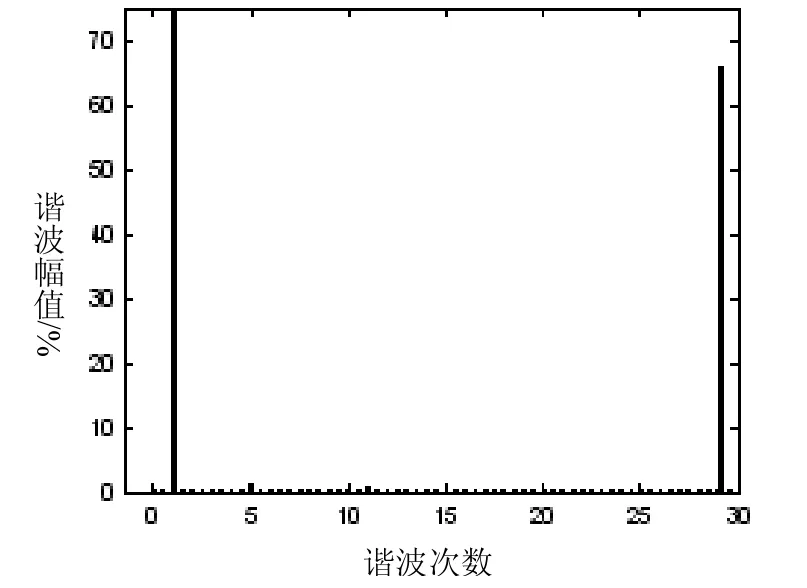
图5 特定谐波消除PWM线电压频谱图
从仿真结果来看,线电压的基波幅值与设定的q值一致,5、7、11、…、6i±1次特定谐波得到了有效的抑制;通过对SHEPWM仿真实验,进一步验证了用计算出的开关角来控制的逆变电源,能够实现抑制特定谐波,对SHEPWM技术的实用化具有一定的参考价值。
本文设计出一功率为500W的PWM逆变器。图6和图7分别为SPWM调制与SHEPWM时输出滤波电容上测量得到的波形,对波形进行分析发SHEPWM技术消除谐波的效果要好于SPWM,这与理论和仿真实验相一致。
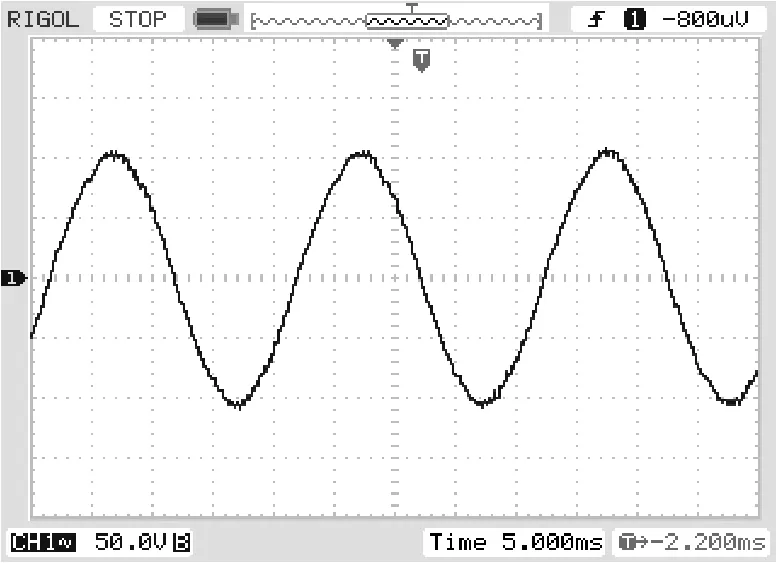
图6 SPWM调制制输出波形
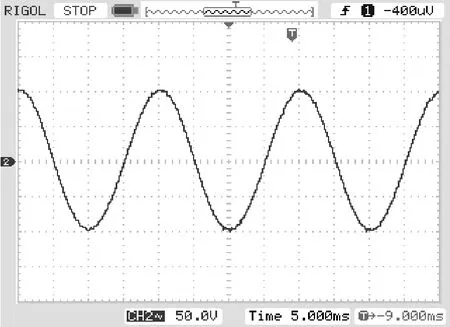
图7 SHEPWM调制时输出波形
6 结论
本文主要分析研究了电压型SPWM逆变器输出电压谐波及其产生规律,并通过仿真进行了验证。从调制法和计算法两个角度分析研究表明:注入适当的三次谐波分量都应是工程应用上较为有效的谐波抑制方法,而且该种谐波抑制方法比较简单,在工程上容易实现;采用SHEPWM技术使逆变电源具有优良的谐波抑制特性,能够从根本上解决谐波抑制问题,随着DSP等处理芯片的快速发展,通过软件、硬件的设计可使SHEPWM这一很有前景的技术尽快走向实用化。
[1]刘凤君.现代逆变技术及应用[M].北京:电子工业出版社, 2006.
[2]吴忠,等.自然采样SPWM电源的谐波分析及抑制策略[J].电网技术, 2001,25(4): 17-20.
[3]HE Yu-yao,LiHong,HeHua.A novelsoft SPWM waveform synthetic method and harmonic analysis[J].Proceedings of the CSEE,2002,22(12):118-122.
[4]孙柯,罗利文,吴晓毅.利用特定消谐技术进行PWM逆变器的设计[J].仪表技术,2007,5:55-57.
[5]费万民,吕征宇,姚文熙.多电平逆变器特定谐波消除脉宽调制方法的仿真研究[J].中国电机工程学报,2004, 24(1):102-106.
[6]洪乃刚等编著.电力电子和电力拖动控制系统的Matlab仿真[M].北京:机械工业出版社, 2006.

