基于Y型阵的互耦矩阵与DOA的同时估计方法

吴彪，陈辉,2，胡晓琴

（1. 空军雷达学院 重点实验室，湖北 武汉 430019；2. 信息综合控制国家重点实验室，四川 成都 610036）

1 引言

空间谱估计是阵列信号处理的一个重要研究方向，其大多数经典的算法，如MUSIC[1]等均是针对等距均匀线阵（ULA）提出并进行讨论的。然而，均匀线阵的最大缺点就是只能提供 0°到 180°范围内的估计，而且由方向图可知其分辨力在线阵法线方向最高，而在轴线方向最差，所以实际的有效范围只有 120°，且只能提供一维角信息；均匀圆阵虽然可以提供 0°到 360°全方位、无模糊的二维角信息，且任何方向上都具有近似相同的估计精度和分辨力，但其阵列流型不具备均匀线阵的Vandermonde矩阵形式，这就使得基于均匀线阵的许多优良算法不能直接应用于均匀圆阵；面阵的阵元数较多，计算量较大，结构比较复杂；L型阵[2]具有均匀线阵和平面阵的特点，结构简单，而且对于均匀线阵的研究成果可用于L型阵，但L型阵和十字阵共同存在的不足是信源DOA方向接近两臂延长方向时，可能会出现前后向模糊[3]（即把方位角误认为其补角），这是阵列结构本身的固有缺陷，虽然可以通过减小阵元间距解决这一问题，但阵列孔径也会同时减小，而且互耦效应也会增加。Y型阵兼有L型阵和圆阵的特点，与L型阵相比，Y型阵可以提供0°到360°全方位、无模糊的二维角信息，任何方向上具有相同的阵列孔径；与圆阵相比，Y型阵的波束宽度更窄，CRB更低，具有更高的分辨精度，与前面几种阵列结构相比，Y型阵在角度一致性、阵列孔径和阵元数方面是个较好的折中。此外，Y型阵列能够灵活扩展孔径，阵元间的互耦效应较小，且在低仰角时不存在前后向模糊[3]。虽然Y型阵作为一种阵列结构已经出现，并实际应用于巨型孔径的光学天文望远镜及射电天文望远镜中，但在阵列信号处理等领域讨论较少。文献[2]中针对L型阵所提出了2-D角估计方法，但没有考虑模型误差的影响。文献[3]讨论了Y型阵列的DOA估计，但用的是矩量法补偿阵元间的互耦，而矩量法有一些固有的缺点。

早期的阵列校正是通过对阵列流型直接进行一系列的测量和内插，但这种方法的效果不太明显，不满足实时性要求。矩量法[4]（MoM）可以严格计算出任意几何形状下阵列的互耦矩阵，但缺点是阵元的电磁参数会随着环境的改变而改变，影响整个系统的工作效率。自校正[5,6]（self-calibration）或在线[7]（on-line）校正算法将互耦的补偿问题转化为一个阵列参数的估计问题，从而实现DOA和互耦矩阵的联合估计，但这类方法通常需要求解一个多维的非线性优化问题，且全局收敛性往往无法得到保证，因此这种方法的容许度较小。文献[8]利用ML-EMSGA的修正遗传算法实现了互耦条件下最大似然估计中似然函数的多维参数估计问题，具有全局收敛的优点。文献[9]利用MP算法估计互耦条件下信源DOA，运算量小，且估计相干源时无需空间平滑，但互耦的补偿用的是矩量法。文献[10]基于RBF神经网络得到了互耦矩阵的快速计算方法，与传统的矩量法相比，这种算法速度快，实时性强，但不能用于非均匀阵列，而且对于复杂环境中线阵的校正需要借助辅助信号源。文献[11]通过设置适量的辅助阵元实现了互耦条件下的DOA估计，但只是针对ULA，其他形状阵列的辅助阵元如何设置没有讨论。本文提出的自校正算法把DOA和互耦系数联合估计问题化为级联估计问题，将多维的非线性搜索降为二维搜索，从而避免了多维搜索带来的庞大运算量和迭代中的全局收敛性问题，且无需辅助信源和任何互耦信息。该方法不仅可以估计Y型阵中线阵内的互耦，还可以估计线阵间的互耦。仿真实验证明了本文所提算法具有运算量小、估计精度高的特点。

2 数据模型

2.1 Y型阵列互耦分析

本文中设置的Y型阵列结构如图1所示，由3个夹角为120°均匀线阵组成，端点处共用一个阵元。设公共阵元位于原点处（O点），阵列位于xoy平面上，其中一个阵位于x轴，另2个阵与x轴正方向的夹角为120°，3个阵的阵元数分别为M1、M2和M3，则总阵元数M=M1+M2+M3-2，阵元间距为d1、d2和d3。假设d1=d2=d3=d=λ/2，3个阵的阵元数相等，M1=M2=M3=M。

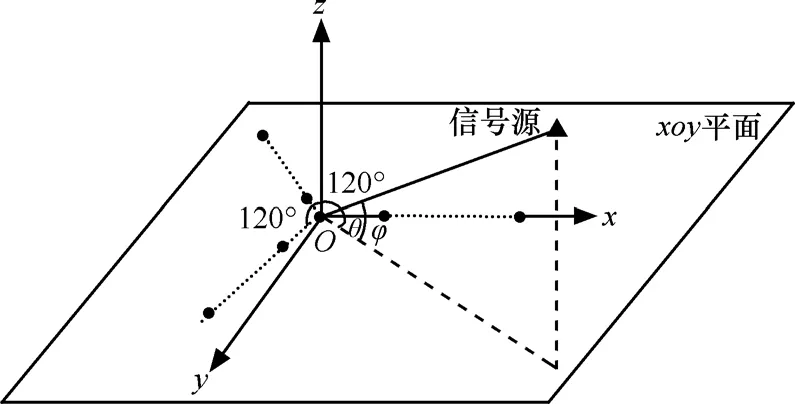
图1 Y型阵列结构（水平放置）

假设C为整个Y型阵列的互耦矩阵

其中，D为阵M×M维线阵内的互耦矩阵，B为M×M维线阵间的互耦矩阵。理想情况下，阵列流型A反映的是阵列在信号方向的空间响应。由于互耦的影响，A不能反映阵列在信号方向的真实空间响应，导致估计性能下降甚至失效。某些互耦系数还会使某一方向的导向矢量是其他几个方向导向矢量的线性组合，从而产生伪峰[11]。

设均匀线阵内的互耦自由度为p，则第一行的系数矢量可表示为

由文献[3,12]可知线阵内的互耦矩阵D可由首1的p维矢量d唯一表征。

其中，Toeplitz( z, z)表示由矢量z组成的对称Toeplitz矩阵。M×M维矩阵B为对称矩阵，但不具有Toeplitz性，所以其阵列结构与D不同，其中第i行，第j列元素Bij可用式(4)描述。

其中，di,j为第i个阵元与第j个阵元的距离，p'=(p-1)d+ε，ε为大于0小于d的常数，该式表示线阵间的阵元间距大于p'时，其互耦效应为0，该值的大小要根据Y型阵列的具体结构合理确定。

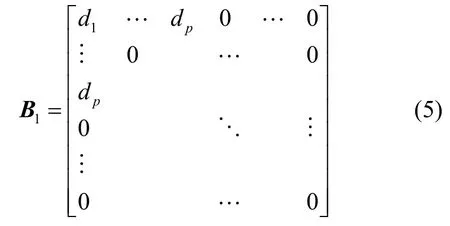
B2是一个第一行和第一列均为0的对称矩阵，它的结构及非零元素的个数都没有很明显的规律，只能根据p值、值和Y型阵列结构具体分析。设[B2]p×p为B2的前p行和前p列组成的矩阵，其余元素为0。这里只给出p=3，=1时的情况。

2.2 互耦存在时的数据模型

如图1所示，假设原点O为参考点，入射信号为窄带远场信号，方位角和俯仰角分别为θi和φi，其中i=1,2,…,N，N为信号源数。设第k个阵元的坐标为(xk,yk)(k=1,2,…,3M)，则

所以第k个阵元相对于参考阵元的相位差为

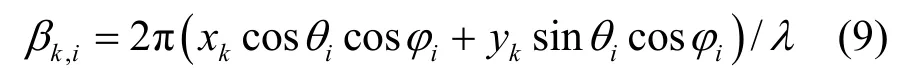
其理想的阵列流型表示为

其中，

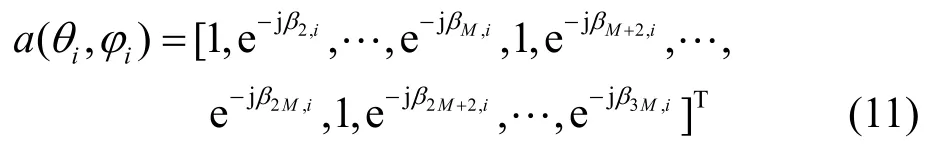
当阵元间距过小或信号频率较高时，阵元间会发生电磁耦合效应，且阵元间距越小，互耦效应越严重。则受到噪声扰动后的阵列接收的快拍数据可表示为

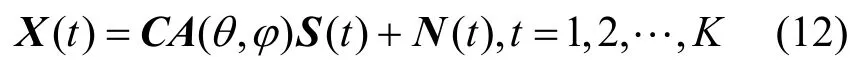
式中，3M×N维矩阵A(θ, )φ满足无秩3M-3模糊，S(t)为N×K维入射信号矢量，3M×K维阵列噪声矢量为N(t)，K为快拍数。信号和阵列噪声均假定为相互独立的零均值平稳Gauss序列。互耦矩阵C维数为3M×3M，具体表达式由式(1)～式(6)给出。

阵列接收数据的协方差矩阵可表示为

由子空间理论的知识可知互耦存在时的MUSIC算法为

3 Y型阵互耦自校正算法

3.1 算法原理

为推导方便，设(θ, φ)=(θi, φi),i=1,2,…,N，相应地，βj=βj,i,j=1,2,…,3M，对于互耦不存在时的导向矢量a(θ, φ)，可以分为

其中，

由式(1)可得存在互耦时的导向矢量。

由于D为带状、对称的Toeplitz矩阵，所以通过矩阵运算可表示为

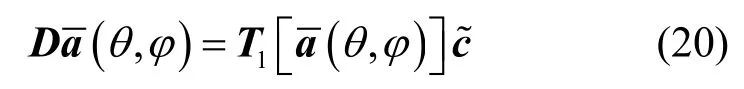
由上节的互耦分析可知线阵间的互耦矩阵B可以分解为B1和B2，则

由矩阵运算可得

T3是一个M×维的重构矩阵。由于矩阵B2的结构及非零元素的个数都没有很明显的规律，只能根据p值、值和Y型阵列结构具体分析，所以M×维矩阵也没有很明显的规律，只能根据矩阵B2的具体结构具体分析。设[T3]p×p表示T3的前p行和前列组成的矩阵，其余元素为0，不表示出来。由式(6)可得

将重构矩阵T1, T2, T3代入式(19)得

由子空间理论有

本文定义如下优化问题来对方位、俯仰参数和互耦系数进行联合估计。

由于互耦系数不全为 0，即c≠0，式(33)成立的充要条件是矩阵 Q ( θ , φ)为奇异矩阵。当p+≤3M-2-N，且阵列导向矢量 a ( θ ,φ,c)满足无秩3M-3模糊时，通常情况下(p +) ×(p +)矩阵Q ( θ , φ)是满秩的，当且仅当(θ , φ)取为信号的真实方位角和俯仰角时才会出现秩损，使其变为奇异矩阵。基于此原理可以得到一种将方位、俯仰估计与互耦系数估计“去耦”的参数级联估计方法。

通过式(35)和式(36)先估计出信号的方位角和俯仰角。

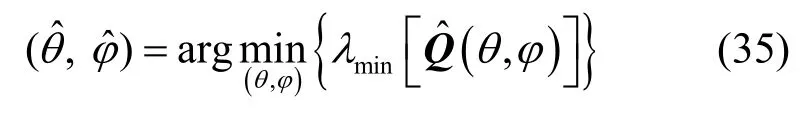
或

其中，λmin[·]为求矩阵最小特征值的算子，det[·]为求矩阵行列式的算子。再利用估计出的方位角和俯仰角 (,)得到互耦系数。

其中，emin[·]为求矩阵最小特征值对应特征矢量子。

3.2 算法步骤

根据以上的分析过程，现将Y型阵列的互耦自校正算法总结如下：

3) 根据式(21)～式(23)计算重构矩阵T1；

4) 根据式(27)计算重构矩阵T2；

6) 根据式(29)计算重构矩阵T；

7) 构造空间谱估计器；

或

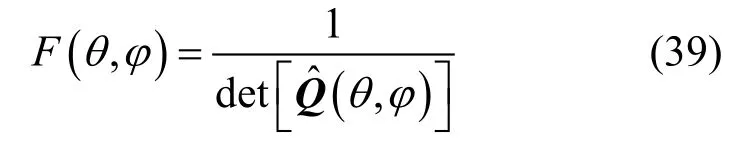
8) 根据式(38)或式(39)搜索谱峰，得到方位角和俯仰角的估计值 ˆˆ(θ, )φ；

9) 根据式(37)得到互耦系数的估计值ˆc。

通过分析发现必须同时校正线阵内和线阵间的互耦才能正确估计DOA。线阵内是一均匀线阵，其互耦矩阵D是一带状、对称的Toeplitz矩阵，线阵间互耦矩阵B是一对称矩阵。基于这些特点，通过矩阵运算，将耦合的角度参数和互耦系数去耦，把联合估计问题化为先估计DOA，再估计互耦系数的级联估计问题。这样的最大优点就是无需求解高维的非线性优化问题，只需进行二维搜索就能解决Y型阵列的二维参数及互耦系数的估计问题。

另外，当线阵内的互耦矩阵自由度p=1时，D为单位阵，B1除了第一行第一列的元素为1外，其他均为0，B2为全零矩阵，本文提出的算法退化为无误差时的二维MUSIC算法。

3.3 算法的模糊性分析

阵列流型是阵列对空域观察区间内单位功率信源响应的集合，它与阵列几何结构和阵列各种电磁参数有着密切关系，是阵列本身固有的一种性质，具体算法对于这类参数的模糊估计是无能为力的，只有通过阵列结构的优化设计或对电磁参数进行某种数值约束[12]。理想均匀线阵在无互耦和其他参数扰动情况下，其导向矢量是理想的Vandermonde矢量，它满足阵列流型无模糊的充要条件是阵列间距小于等于半波长。互耦存在时，由于互耦参数与理想导向矢量耦合，阵列流型几何性质发生了变化，此时阵列流型保证无模糊的条件很难进行理论分析，下面给出经过大量仿真实验得出的结论。

假设均匀线阵不存在模糊（即阵元间距小于等于λ/2），互耦自由度p,满足下列条件：

4 仿真实验

Y型阵的阵列结构如图1所示，共有22个阵元，阵元间距均为半波长。p=3，= 1 ，d = [ 1,0.7821+0.258 3i,- 0 .547 6 + 0.246 9i]T， b = [ 0.652 4-0.2478i]T，互耦系数是随机选取的，噪声为零均值的高斯白噪声，2个信号源为非相干源，方位角分别为 20°和 40°。

仿真1：Y型阵列的互耦自校正算法的空间谱曲线。在快拍数为100，信噪比为10dB的条件下，图 2(a)为互耦未补偿和互耦已知时的 MUSIC算法以及本文提出的SAY算法（最小特征值法，SAYE和行列式法，SAYD）空间谱曲线的比较。图 2(b)给出了只校正线阵内互耦时的谱，此时，式(29)中的是维数为M×的全零矩阵。

图2 空间谱曲线

图2（a）表明互耦存在时，MUSIC算法失效，而本文提出的算法和互耦已知时的MUSIC算法均可以准确地估计信号的DOA。图2（b）表明只校正线阵内的互耦，无法获得理想的效果，只有同时校正线阵内和线阵间的互耦时，才能得到理想的估计性能。

仿真2：方位角估计性能随信噪比变化的曲线。快拍数为100时，比较SAYE、SAYD算法和互耦已知时的MUSIC算法与信噪比的关系。每个信噪比做100次Monte-Carlo仿真实验，比较DOA估计的成功概率和均方根误差（RMSE）与信噪比的关系，并在图3(a)和图3(b)中分别给出了两者的变化曲线。2个信号源DOA的估计值与真实值的误差均在0.5°内时视为成功。

图3(c)给出了互耦已知MUSIC算法、SAYE算法与互耦已知和互耦未知时的 CRB随信噪比的变化曲线。

图3 估计性能与信噪比关系

图3(a)～图3(c)说明了SAYE算法和SAYD算法的性能曲线非常接近。SAY算法的估计性能要稍差于互耦已知时的MUSIC算法，但当信噪比变大时，三者的曲线基本重合，性能趋于一致。这表明了互耦未知的条件下，本文所提算法也可以获得较高的估计性能。

仿真3：互耦系数的估计性能。参数设置同仿真2。表1给出的是SAYE算法在不同信噪比条件下，通过100次Monte-Carlo仿真实验，其中互耦系数为

互耦系数矢量的相对校正误差定义为

从表 1和图 4(a)、(b)中可以看出信噪比大于15dB，快拍数大于100时，Y型阵列的 ρcoupling很小，并且随着信噪比的增加， ρcoupling逐渐趋近于零，即互耦系数矢量的估计值逐渐趋于真值。

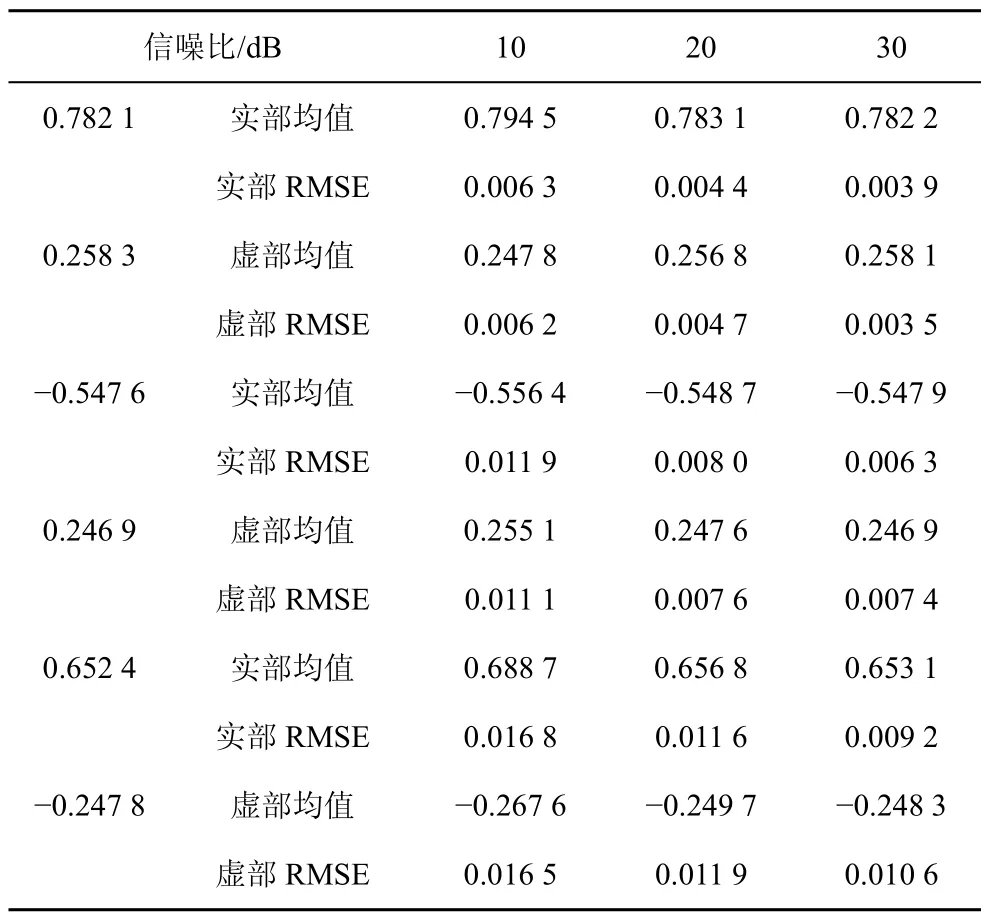
表1 互耦系数估计值与信噪比的关系

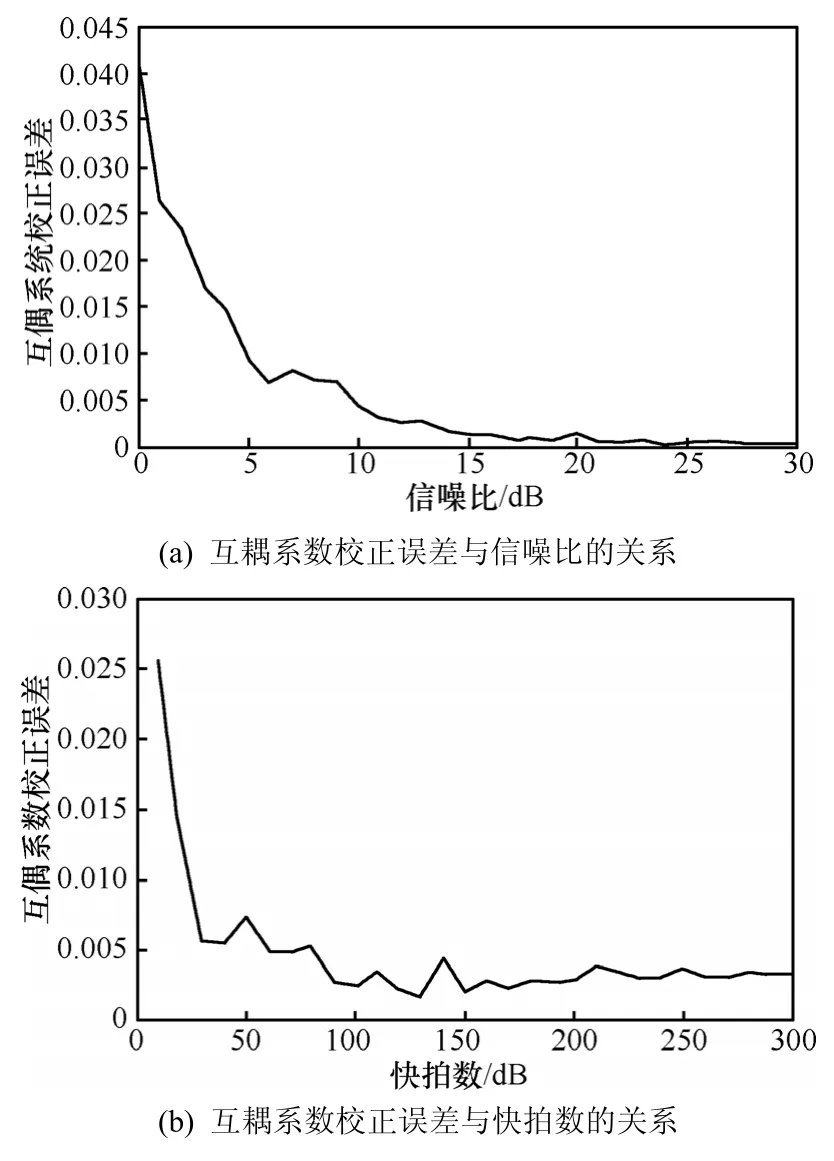
图4 估计性能与快拍数关系

5 结束语

本文针对Y型阵列的特殊结构，对互耦矩阵进行了详细分析，建立了互耦条件下的数据模型，并基于子空间原理，提出了一种基于Y型阵列互耦条件下非相干源的DOA估计及互耦自校正算法。该算法把相互耦合的DOA和互耦系数的联合估计问题转化为“去耦”的级联估计问题，避免了传统自校正算法运算量大，全局收敛性无法保证等问题，很好地解决了Y型阵列的互耦问题。理论分析和仿真结果均表明了本文提出的自校正算法的DOA估计不需要互耦矩阵的任何信息，具有估计精度高、分辨力强等特点，并且在DOA估计的同时，还可以精确地估计出互耦矩阵，从而实现Y型阵列的自校正，具有较大的实际意义。

[1] SCHMIDT R O. Multiple emitter location and signal parameter estimation[J]. IEEE Transactions on Antennas and Propagation, 1986,34(3): 276-280.

[2] HUA Y, SARKAR T K, WEINER D D. An L-shaped array for estimating 2-D directions of wave arrival[J]. IEEE Transactions on Antennas and Propagation, 1991, 39 (2): 143-146.

[3] ELLINGSON S W. Design and evaluation of a novel antenna array for azimuthal angle-of-arrival measurement[J]. IEEE Transactions on Antennas and Propagation, 2001, 49(6): 971-979.

[4] YUAN Q W, CHEN Q. Accurate DOA estimation using array antenna with arbitrary geometry[J]. IEEE Transactions on Antennas and Propagation, 2005, 53(4): 1352-1357.

[5] FRIEDLANDER B, WEISS A J. Direction finding in the presence of mutual coupling[J]. IEEE Transactions on Antennas and Propagation,1991, 39 (3): 273-284.

[6] SELLONE F, SERRA A. An iterative algorithm for the compensation of toeplitz mutual coupling in uniform and linear arrays[A].12th-signal Processing Education Workshop, Digital Signal Processing Workshop[C]. 2006. 438-443.

[7] LIN M, YANG L X. Blind calibration and DOA estimation with uniform circular arrays in the presence of mutual coupling[J]. IEEE Antennas and Wireless Propagation Letters, 2006, 5: 315-318.

[8] ZHANG T T, LU Y L, HUI H T. Compensation for the mutual coupling effect in uniform circular arrays for 2D DOA estimations employing the maximum likelihood technique[J]. IEEE Transactions on Aerospace and Electronic Systems, 2008, 44(3): 1215-1221.

[9] ELKAMCHOUCHI H M, OMAR M M M. An efficient computational approach in the matrix pencil method to find one dimensional and two dimensional direction of arrival[A]. National Radio Science Conference 2007[C]. Cairo, 2007.1-8.

[10] 于斌, 尹成友, 黄冶. 基于RBF神经网络的互耦逆矩阵快速计算方法[J]. 电子与信息学报, 2008, 30(6): 1496-1499.YU B, YIN C Y, HUANG Y. A fast computation method of mutual coupling inverse matrix based on RBF neural network[J]. Journal of Electronics & Information Technology, 2008, 30(6): 1496-1499.

[11] YE Z F, LIU C. On the Resiliency of MUSIC direction finding against antenna sensor coupling[J]. IEEE Transactions on Antennas and Propagation, 2008, 56(2): 3741-380.

[12] 王布宏, 王永良, 陈辉等. 均匀线阵互耦条件下的鲁棒 DOA 估计及互耦自校正[J]. 中国科学 E辑. 技术科学, 2004, 34(2): 229-240.WANG B H, WANG Y L, CHEN H, et al. A robust DOA estimation algorithm for uniform linear array in the presence of mutual coupling[J].Science in China Ser E Technological Science, 2004, 34(2): 229-240.