基于圆自卷积的主载波捕获算法

吴建强， 詹亚锋， 颜学龙， 陆建华

（①桂林电子科技大学 电子工程学院，广西 桂林 541004；②清华大学 宇航技术研究中心，北京 100084）

0 引言

统一测控体制中，需要首先捕获主载波的频率，以实现下行信号的接收。在深空探测中，航天器高速飞行，具有很大的径向速度和加速度，使下行信号产生特别严重的多普勒频偏和多普勒频偏变化率，前者高达信息速率的几十倍甚至几百倍，后者高达信息速率的几倍甚至几十倍；另外，为了充分利用探测器的有限发射功率，必须增大信号的调制度，当调制度大于1.4时主载波频谱幅度将小于副载波频谱幅度，导致主载波的捕获更加困难。大调制度下主载波的捕获方法，成为目前深空通信领域的研究重点，同时也是一个研究难点。

在现有的深空通信系统中，主载波捕获采用的方法主要有判最大值法、频率扫描法[1]、频谱模板匹配法、频谱能量中心法[2]、判频谱对称法[3]等。其中，判最大值法实现简单，但只适合小调制度下的主载波捕获；频率扫描法需要根据扫频控制的步进精度设计环路滤波器的捕获带宽，步进小，扫描速度慢，载波锁定时间长，步进大，环路滤波器捕获带宽大；频谱模板匹配法需要预先知道信号模板，而信号模板在实际应用中很难获取；频谱能量中心法有一个前提——载波能量中心和频谱的对称中心重叠，但当有噪声和多普勒频偏存在时，这个前提不成立；判频谱对称法是一种适合工程应用的方法，但目前还没有一种较好的具体实现算法。

文献[3]中提出了一种基于判频谱对称法的伪对称点最小误差判定方法。仿真结果显示，该方法能够在大调制度下有效捕获主载波的位置。但是，该方法需要在最大多谱勒频偏范围内逐一假设对称点，完成一次主载波捕获需要的加法次数为：

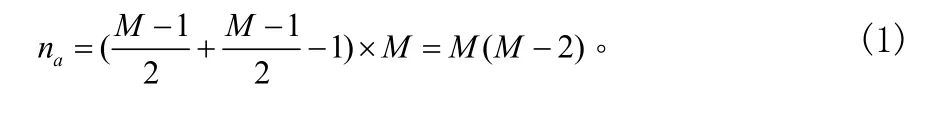
为了提高主载波的搜索精度必须保证M值足够大，在工程应用中一般取M为2048～4096点,那么完成一次主载波捕获需要的加法次数为4190208～16769024次,这几乎无法实现。

综上所述，深空测控通信领域急需一种抗噪声能力强、正确捕获概率高、适应大调制度、计算量适中且适合工程实现的主载波捕获方法，以提高接收机的抗多普勒频偏性能。针对判频谱对称法，本文提出一种基于圆自卷积的主载波捕获算法。

1 算法分析

微波统一测控体制的信号为：

其中，A为载波幅度；wC为主载波角频率；mi为第i个副载波对主载波的调制度；wi为第 i个副载波的角频率；ai(t)为原始调制码元。

从文献[2]中可知，此信号频谱中除了含有主载波分量wC外，还存在无穷多个频率为(wC+ niwi)的分量、无穷多个频率为(wC+∑niwi)的交叉分量，它们都对称分布在主载波分量两侧。可见，信号频谱是以主载波为中心呈左右对称分布的，依次为副载波和副载波的谐波频谱。因此，通过判频谱对称法确定主载波频率是一种适合工程应用的方法。

圆卷积是利用圆周时间反转运算的卷积，其表达式为：

其中，x2((n-m))NRN(n)为 x2(n-m)周期延拓后的主值序列。如果 x1(n)=x2(n)，则式(3)为圆自卷积表达式，假设 x1(n)=x2(n)= x(n)，则有：

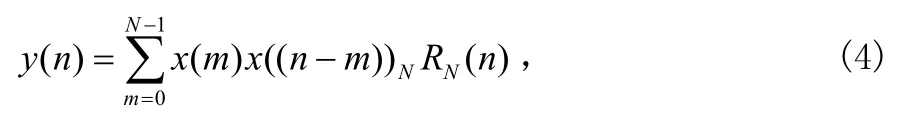
假设h(n)为x(n)周期延延拓后以原点为对称点翻转的主值序列，即：

将式(5)代入式(4)，有：

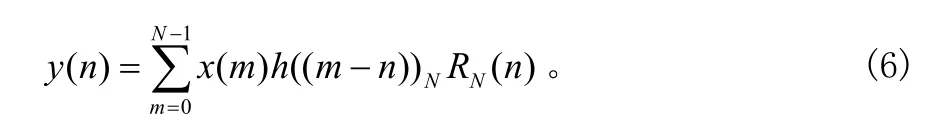
式(6)即为 h(n)和 x(n)的圆互相关表达式，可见，x(n)圆自卷积即为x(n)周期延延拓后以原点为对称点翻转的主值序列和x(n)的圆互相关。众所周知，互相关是两个函数间存在相似性的量度。由互相关函数的性质可知，x(m)与 h((mn))NRN(n)越相似，其相关函数 y(n)越大；即 x(n)和 x(n)周期延延拓后以原点为对称点翻转的主值序列越相似，其相关函数 y(n)越大。如果 x(n)是圆周 N内以 m为对称点呈圆周对称的信号，则x(n)周期延延拓后以原点为对称点翻转的主值序列就是圆周 N内以(N-m)为对称点呈圆周对称的信号，此时只要将x(n)周期延延拓后以原点为对称点翻转的主值序列圆周右移 2m点即和 x(n)完全重叠，因此相关函数 y(2m)最大。

由上可知，通过判定圆自卷积结果的最大值即可确定信号频谱的对称点位置。由于采样信号计算频谱前做了下变频，消除了主载波角频率wC，因此当多普勒频偏为x Hz时，信号频谱在圆周N内以(xN/fs)点为对称点呈圆周对称,其中fs为采样频率，N为计算频谱时做FFT变换取的点数，此时相关函数y(2xN/fs)最大。当0≤x＜fs/2时，相关函数y(2xN/fs)最大；当fs/2≤x＜fs时，相关函数y(2(x- fs/2)N/fs)最大。因此，当0≤x＜fs/2时，多普勒频偏为x Hz和(x+ fs/2) Hz的相关函数均为y(2xN/fs)最大，这样就无法区分多普勒频偏是x Hz还是(x+ fs/2) Hz。为了区分这两种情况，必须保证多普勒频偏范围内不会出现两个频率点使同一点的相关函数值最大，即多普勒频偏范围必须小于采样频率fs/2，这正是避免频谱混迭需要满足的奈奎斯特定理。

直接计算圆自卷积计算量很大，完成一次主载波捕获需要的乘法次数为N2个，需要的加法次数为N(N-1)个。为了提高主载波频率的搜索精度必须保证N值足够大，在工程应用中一般取N为2048～4096点，则此算法的计算量将远超过伪对称点最小误差判定方法的计算量,在工程中更是无法实现。

但是，圆自卷积可以利用 FFT实现。由圆卷积定理可知，序列的圆自卷积的离散傅里叶变换等于此序列离散傅里叶变换的平方，即若：

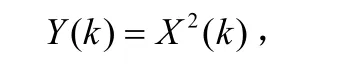
则：

因此，对频谱做 FFT变换后取平方，然后做 IFFT变换，此序列即为频谱的圆自卷积结果，通过判定此序列最大值可确定信号频谱的对称点位置，即主载波频率。

2 算法仿真及性能分析

假设调制信号只有一个副载波，即式(2)中 k为 1，并且其副载波调制频率为 32 kHz，副载波调制方式为未成型的BPSK调制，原始调制码元的信息速率为1 kb/s。由于在主载波捕获前对接收信号进行了下变频，因此进行主载波捕获的主载波角频率就是多普勒频偏，假设多普勒频偏为100 kHz，则进行主载波捕获的信号表达式为：

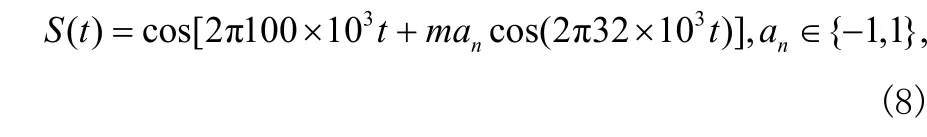
其中m为调制度，an为信息速率为 1 kb/s的原始调制码元。通常深空通信中，多普勒频偏范围为±150 kHz，根据奈奎斯特定理，采样率选为 800 kHz，并分别做 2048点和4096点的FFT，经过n次平均(n分别取1，2，4，8)后得到信号的平均频谱E(k)，然后对E(k)采用圆自卷积算法捕获主载波的位置，统计 100次，得出调制度分别为 1.4和 1.9时，副载波（功率为C）处于各种载噪比C/N0[4]条件下一次捕获主载波的概率曲线图，如图1～图4所示。

图1 8次平均4096点FFT的一次捕获概率曲线

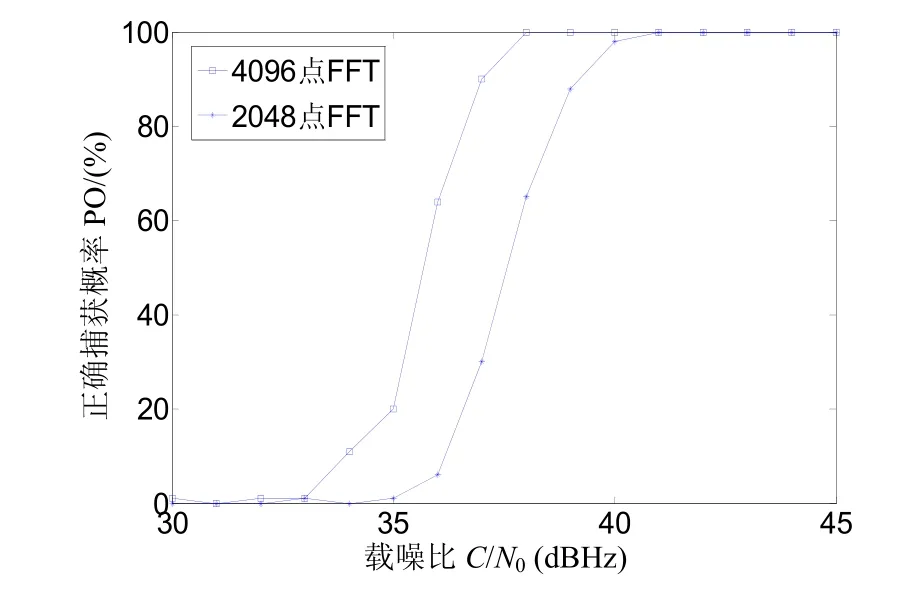
图2 8次平均调制度1.4的一次捕获概率曲线

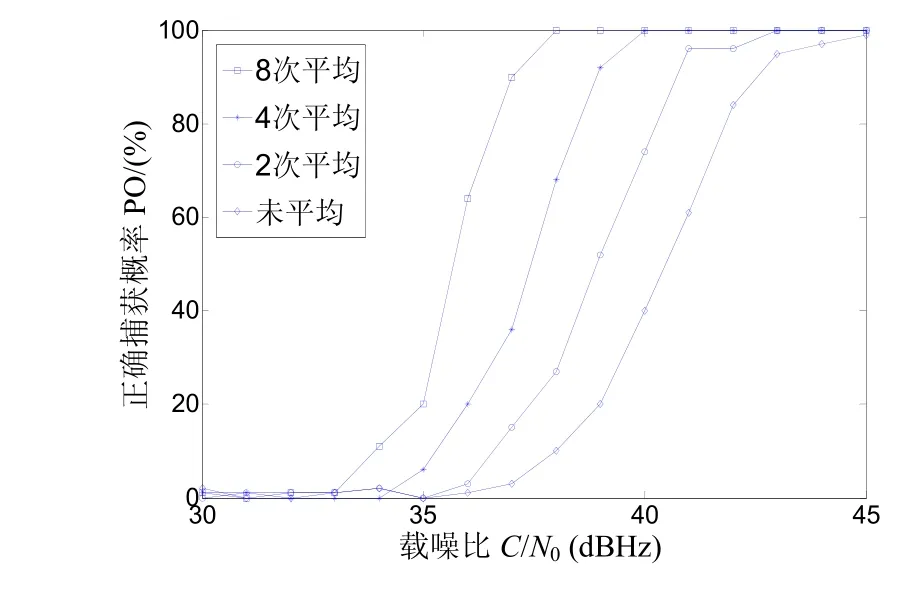
图3 4096点FFT调制度1.4的一次捕获概率曲线

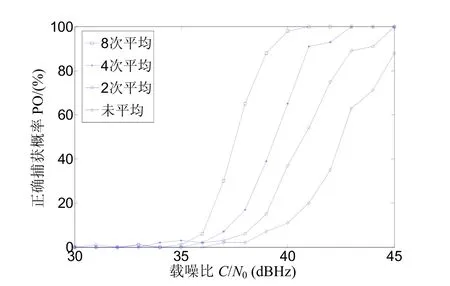
图4 2048点FFT调制度1.4的一次捕获概率曲线

图 1为 4096点 FFT变换，频谱平均 8次，调制度为1.4和 1.9条件下一次捕获主载波的概率曲线图。调制度为1.4和 1.9时，分别在载噪比C/N0≥38 dBHz和≥40 dBHz时，一次主载波正确捕获的概率为 100%。可见，调制度为1.9时比 1.4时主载波捕获的性能降低2 dB。但是，当调制度增大时，副载波能量将增大，副载波载噪比也随之增大，因此，该算法在大调制度下依然适用。

图 2为调制度为 1.4，频谱平均 8次，2048点和 4096点 FFT变换条件下一次捕获主载波的概率曲线图。2048点和 4096点 FFT变换分别在载噪比C/N0≥40 dBHz和≥38 dBHz时，一次主载波正确捕获的概率为 100%。可见，2048点比4096点FFT变换主载波捕获的性能降低2 dB左右。从这一点看，资源足够时应该选择更多点 FFT变换的圆自卷积法。但是 FFT变换点数越多，一次主载波捕获时间越长，而深空通信中多普勒频偏变化率很大，当主载波捕获时间过大将导致很大的捕获误差，如果该误差超过后续的主载波跟踪环路带宽将导致主载波失锁，整个系统无法正常工作。因此，在设计主载波捕获方案时应选择合适的FFT变换点数以达到最佳的主载波捕获性能。

图3、图4分别为2048点和4096点FFT变换，调制度为 1.4，频谱平均n次(n分别取 1，2，4，8)条件下一次捕获主载波的概率曲线图。可见，不管 FFT变换点数为 2048点还是 4096点，对频谱平均次数每增加一倍，圆自卷积法在主载波捕获上的性能都提高 2 dB左右。由于频谱平均次数越多，抑制白噪声能力越强，因此增加频谱平均次数将提高主载波捕获性能。从这一点看，在设计主载波捕获方案时应该尽量增加频谱平均次数。但是，增加频谱平均次数必然导致增大主载波捕获时间。前面已分析，一次主载波捕获时间不能过长，因此，在设计主载波捕获方案时同样要选择合适的频谱平均次数。

通过对深空通信中的调制信号在各种情况下利用圆自卷积法实现主载波捕获的分析可知，圆自卷积法可以实现各种调制度下的主载波捕获。在设计圆自卷积法实现主载波捕获方案时，应综合考虑硬件资源和系统需求选择合适的 FFT变换点数和频谱平均次数。当以上选择均为最佳时，将能实现各种调制度下的最佳主载波捕获性能。

3 FPGA验证

作者把上述算法在 Xilinx的 FPGA——XC4VLX60平台上进行了实现。通常深空通信中，多普勒频偏范围为±150 kHz，根据奈奎斯特定理采样率选为800 kHz。圆自卷积法的主载波捕获首先需要一个 FFT模块和两个乘法器计算出信号频谱，然后利用 FFT变换实现圆自卷积需要一个FFT模块、一个 IFFT模块和三个乘法器；而 Xilinx的XC4VLX60中，DSP资源为 64个[5]，一个乘法器占一个DSP资源，2048点基 2FFT占 6个 DSP资源，基 4FFT占18个DSP资源，流水线FFT占28个DSP资源。假设多普勒频偏变化率最大能达到 50 KHz/s，而以 800 kHz的采样率采2048点需要2.56 ms，采4096点需要5.12 ms，信号频谱最大捕获误差见表1。

由表 1的分析可知，在硬件平台为 XC4VLX60下，基4FFT变换为最佳选择。而主载波捕获的后续主载波跟踪环路带宽通常为1KHz时性能较佳，由表1针对不同频谱平均次数下最大捕获误差的分析可知，2048点 FFT变换、4次平均和 4096点 FFT变换、2次平均都是较好的选择。

表1 各种实现方案在FPGA内的DSP资源占用率及其捕获性能分析表

4 结语

为了对抗深空测控通信中的多普勒频偏，本文提出一种利用对称频谱、基于圆自卷积的主载波捕获算法。仿真结果和 FPGA实现验证了这种主载波捕获算法能够有效消除大调制度下的多普勒频偏，并且根据硬件资源和系统需求选择合适的 FFT变换点数和频谱平均次数能够实现低载噪比下的主载波捕获，在2048点基4FFT变换、4次信号频谱平均时，能够在调制度为 1.9，载噪比C/N0≥45 dBHz时一次正确捕获概率达到100%，且在FPGA内实现时占用的DSP资源为 59个。因此，它适用于深空通信中各种调制度下多普勒频偏的快速估计，且适合FPGA实现。

[1] 王福昌,鲁昆生. 锁相技术[M]. 武汉：华中科技大学出版社,1997.

[2] 李海涛. 微波统一测控系统载波捕获防错锁技术研究[D]. 长沙：国防科学技术大学，2002

[3] 赖卫东，詹亚锋，陆建华. 大调制度微波统一测控系统载波捕获算法[J]. 清华大学学报，2009(07):940-943.

[4] Paul Collins, Peter Stewart. GPS SNR Observations[R].Canada: Geodetic Research Laboratory, 1990.

[5] Xilinx Inc. Virtex-4 Family Overview[R]. USA: Xilinx Inc.,2007.