复杂网络攻击与修复策略

崔强 谭敏生 王静

南华大学计算机科学与技术学院 湖南 421001

0 前言

随着复杂网络研究的兴起，作为复杂网络最重要的课题之一，对复杂网络攻击与修复策略的研究的重大理论意义和应用价值日益凸显出来，人们开始关注：这些复杂的网络到底有多可靠？在网络遭受攻击后如何高效快速的修复网络？例如2008年1月25日，在持续了十多天的冰雪天气后，湖南、浙江、安徽、江苏、福建、湖北、四川、重庆、贵州、云南、广西、广东等电网的电力设施均遭到不同程度破坏，局部地区由于电力设施毁坏严重使电力供应中断达数天之久。电网和交通的瘫痪使一些县城、乡镇成了孤岛，交通瘫痪、电力中断、供水停止、燃料告急、食物紧张。那么当出现此种情况后如何快速修复我们的生命线网络就变得尤其重要。

1 攻击策略

复杂网络通常面临两种攻击：随机性攻击(Random attack)和选择性攻击(Selective attack)。所谓随机性攻击就是网络节点(边)以某种概率被随机的破坏；而选择性攻击是网络节点(边)按一定的策略被破坏，一般按照节点的度值大小依次去除节点。一般来说，网络自身原因引起的故障属于随机性攻击，而蓄意的破坏则属于选择性攻击。例如，敌人在选择攻击目标时，总是先选择重要的军事目标，而不是随机破坏。所以研究攻击策略的效率，时效性就变得很有意义。

1.1 基于不完全网络拓扑信息的有目的攻击

有关攻击策略的仿真研究中，比较全面的要数Holme等的研究工作。他们将攻击策略分为节点攻击与边攻击两种方式。每种攻击又包括四种不同的策略：①ID移除策略。对初始网络按节点或边的度大小顺序来移除节点或边；②IB移除策略。对初始网络按照节点或边的介数大小顺序来移除节点或边；③RD移除策略。每次移除的节点或边是当前网络中节点或边的度最大的节点；④RB移除策略。每次移除的节点或边是当前网络中节点或边介数最大的节点。ER模型对节点的基于度的攻击比基于介数的攻击效果好，使用重新计算的信息比基于原始信息的危害性更强 ；而对边的攻击RB远比其他策略更具破坏性。无尺度网络对节点移除比ER模型更敏感，在攻击初期四种策略的差异性不明显，随着移除的继续进行，攻击对网络的破坏程度按以下顺序排列：RB>RD>ID>IB；而且对边的攻击情况同节点攻击相似。作者还对Internet等真实网络作了数字分析，验证了Albert等的结论。

1.2 基于局部网络拓扑信息的分布式攻击

分布式攻击能逐步在网络上传播，攻击已经“沦陷”节点的邻节点，且下一个攻击目标的选择仅仅需要节点的局部信息——被攻击节点的邻节点的度值信息。如果一个节点被攻击，本文称之为“沦陷”节点，否则称之为“存活”节点。

本文基于Internet真实子网和BA网络模型(网络模型同上)，对以下3种分布式攻击策略的攻击效率进行仿真测试：

（1）贪婪顺序攻击：选择与上一步被攻击节点相连的最大度值“存活”节点作为攻击目标。如果没有这样的节点存在，则随机选择一个“存活”节点作为攻击目标。

（2）协同攻击：搜索“沦陷”节点的“存活”邻节点，在它们中选择一个最大度值的“存活”节点作为攻击目标。如果没有这样的节点存在，则随机选择一个“存活”节点继续展开攻击。

（3）限下界平行攻击：不同于每步只攻击一个与“沦陷”节点相邻的最大度值节点，而是攻击所有满足以下两个条件的“存活”节点：与“沦陷”节点邻接；度值在预先设定的界值之上。

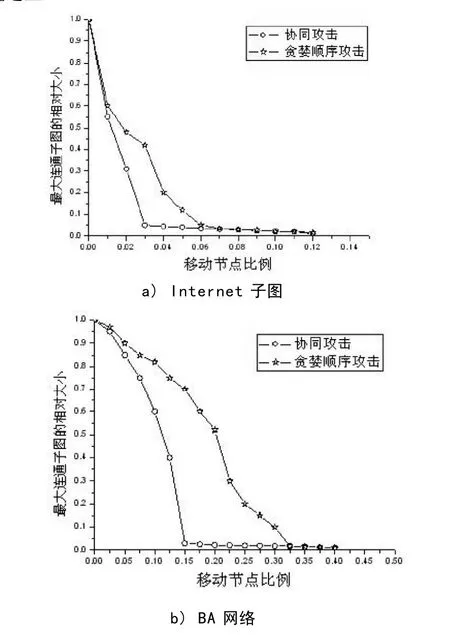
图1 贪婪顺序攻击和协同攻击的攻击效率

图1比较了贪婪顺序攻击和协同攻击各自的攻击效率。结果表明，贪婪顺序攻击并不能高效地击垮整个网络，相反，仅利用局部信息的协同攻击却能得到与有目的攻击差不多的崩溃阈值。这个观察结果可以这样理解，在贪婪顺序攻击中，因为没有中心节点与刚刚沦陷的节点相邻，大量攻击步骤都不得不攻击许多小度值的节点。在协同攻击中，每一步能够在比较多的节点中选择下一步的攻击目标，因此，很少会需要攻击小度值的节点。协同攻击最主要的缺点就是，为了找到下一个攻击目标，在攻击前要收集所有“沦陷”节点的度值信息。

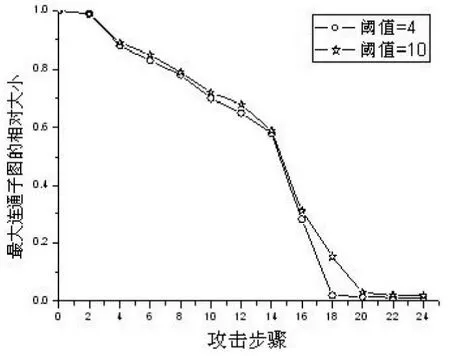
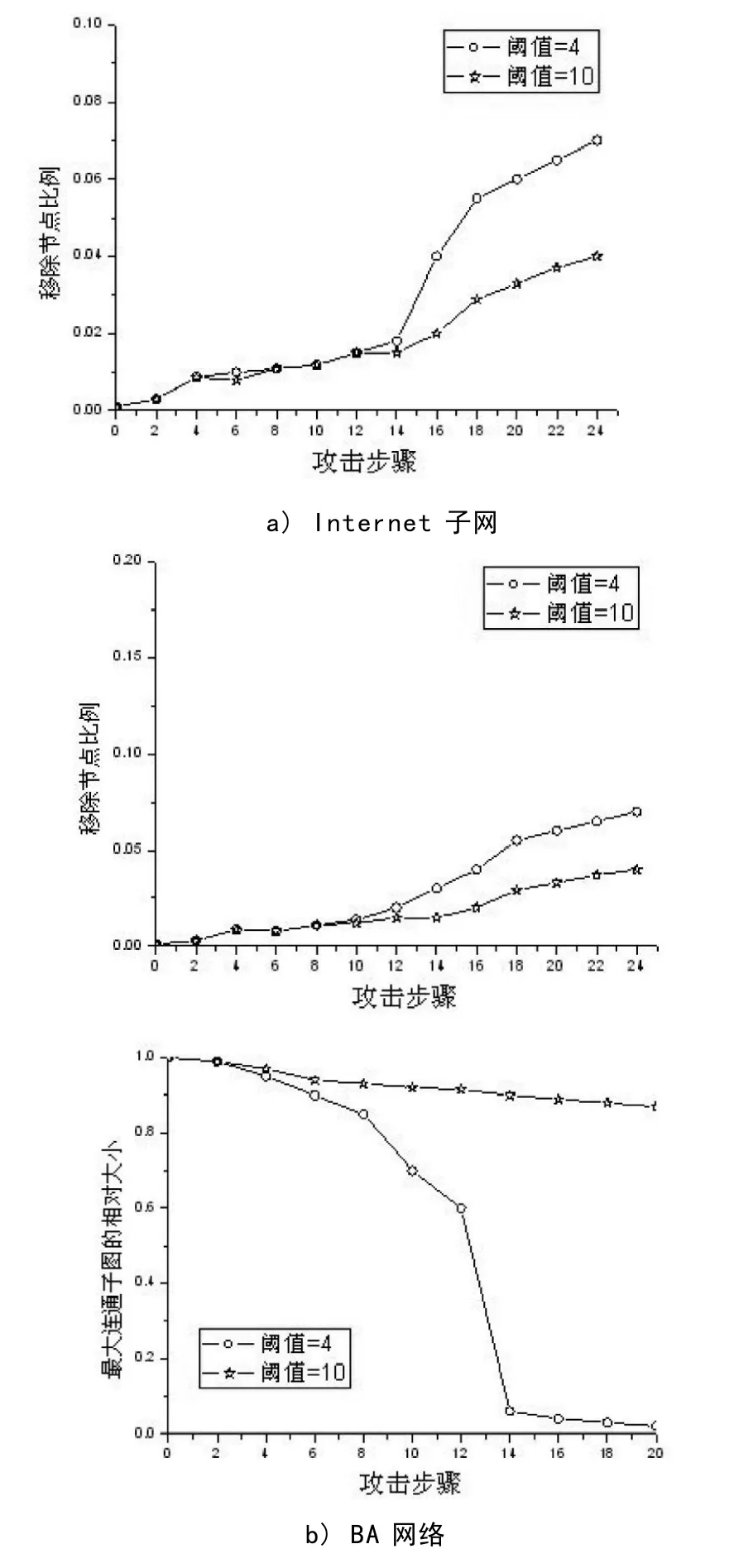
图2 平行攻击的攻击效率

为了减少攻击前节点间非常复杂的协作和信息交换，本文提出了限下界的平行攻击。这种攻击方式非常类似于现实世界的攻击。为了避免攻击许多低度值的节点，本文设定的下界值分别是4和10，也就是说与上一步被攻击节点邻接的节点的度值大于4和10时，才会被攻击。

仿真结果如图2所示。在Internet模型中，下界值为10的攻击和有目的攻击一样高效，崩溃阈值从3.8%只轻微上升到4.1%。假如设置的下界值是4，在网络崩溃前，攻击节点数增多(崩溃阈值变为5.7%)，并且由于每一步攻击的节点数增多，攻击的步骤减少。在BA模型中观察的结果是不同的，如果下界值设定为4，崩溃阈值非常接近于有目的攻击(崩溃阈值为16%)。当下界值设定为10，攻击将在17步后终止，因为这时所有“沦陷”节点的存活邻节点的度值都低于下界值，此时，网络还存在较大的连通子图。

可以这样理解所观察到的结果，仅仅掌握Internet局部网络拓扑信息，只攻击度值相对大的节点，同样可以摧毁整个网络。从图2可以看出，在早期，网络分解速度较慢，在某些步骤以后，分解的速度急剧加快。因此，为了保护Internet免遭这种分布式攻击的破坏，关键在于尽早识别并阻止攻击。此外，选择合适的阈值对攻击方非常重要：太低的阈值需要攻击更多度值小的节点，使攻击速度变慢，攻击时间延长，这样一来防御方有机会加强保护，甚至对攻击者予以反击；而设定太高的阈值使攻击的破坏程度降低，甚至不可能摧毁整个网络。

2 复杂网络修复策略

目前国际和国内虽然对网络的修复性有一定研究但对复杂网络遭到破坏的研究还只局限于研究复杂网络的鲁棒性，即复杂网络对外界的破坏的承受能力。即使一些文章中涉及到复杂网络的修复性研究但其修复策略和一般网络的修复策略也没什么区别，而我们首次针对复杂网络的幂率分布特性提出了一种基于马太效应的复杂网络修复策略。

2.1 相关研究

（1）在文献[3]中总结了基于拓扑信息的修复策略，在此种修复策略中分析拓扑图论与网络生存性的关系，介绍拓扑图论算法在网络修复中的实际应用，对基于网络分割的故障修复算法、基于拓扑结构的修复路径选择算法、用于链路故障保护的P-Cycle 算法等进行比较，研究和探讨了目前网络修复中亟待解决的问题。网络的修复与网络的生存性密切相关，但从目前的研究成果来看，两者的结合还不够，而且大多数研究考虑的拓扑结构简单、故障种类单一。目前的网络拓扑研究在物理拓扑和逻辑拓扑上是混淆的。这就导致了基于网络拓扑结构的修复算法难以用实验仿真也难于实现，而且从大型实际网络中测量其全部拓扑也存在一定的难度这就导致了此种修复策略的实用性不高。

（2）以一定的修复几率重新连接遭到袭击的节点和网络中的其它节点。在其修复模型中是以一定的修复几率来修复网络的并没有考虑复杂网络本身的一些特性这就使得此种修复模型的针对性不强，而我们的修复策略充分考虑了复杂网络的幂率特性及其在随机重连时的马太效应，所以我们的修复策略更具有针对性。

（3）网络修复过程中的评价标准：最大效率法和Horn算法。对网络修复算法提出了量化的评价标准。

2.2 基于马太效应的复杂网络修复方法

近年来在复杂网络研究上的一重大发现是许多复杂网络，包括Internet、WWW以及新陈代谢网络等的链接度分布函数具有幂率形式。BA网络模型能很好的反映这一特性，BA网络模型的生成过程很好的考虑了实际网络的以下两个特性 ：

（1）增长(growth)特性：即网络的规模不断扩大。

（2）优先连接(preferential attachment)特性：即新的节点更倾向于与那些具有较高连接度的“大”节点相连接。这种现象也称为“马太效应(Matthew effect)”。

我们从无标度网络的马太效应出发研究马太效应在复杂网络修复中的应用。我们主要考虑持续攻击下的随机删除节点和有目的删除节点(比如删除网络中的最大度值节点)，在这种攻击中以比率r优先选择删除一个节点的同时把一个节点重新连接到网络上，我们假设新加入到网络中的节点选择网络中度值最大的节点连接。失去邻接点的节点不是坐以待毙而是重新连接其他节点来代替丢失的邻节点；此外，被攻击的节点作为新节点重新连接到网络中。这样，当攻击网络的最大度值节点时，补偿动力学协议仍然能够保护密率分布的指数。而且，我们的仿真显示即使在很高比率的优先攻击下或攻击网络中的大度值节点时，只要新加入的节点拥有m≥2的随机连接网络就能够保持一个很大的连接部分；这样，失去的连接就不再是这个持续攻击的损害结果。

我们是把构建BA网络的思想应用到幂率分布网络的修复中能得到很好的效果，这不仅能得到很高的修复率而且还能优化网络的拓扑结构。我们的方针结果显示在此种修复方法下对internet网络和BA网络的修复率可达98%以上，即使攻击网络中的最大度值节点修复率也可达到95%以上。

3 结论

本文分别研究了基于不完全网络拓扑信息的有目的攻击和局部网络拓扑信息的分布式攻击下以及有关复杂网络修复策略的相关研究并提出了基于马太效应复杂网络修复策略，该研究对于制定高效的攻击策略和修复策略具有重要的意义特别是在军事领域具有很高的实用价值。

[1] Watts D J,Strogatz S H.Collective dynamics of small-world networks[J].Nature.1998.

[2] Holme P, Kim B J, Yoon C N, et al. Attack vulnerability of complex networks[J]. Phys.Rev.E.2002.

[3] 缪志敏,丁力等.基于拓扑信息的网络修复[J].计算机工程.2009.