基于轨迹模块设计的捷联惯导仿真研究*
刘文远 李 恒 丁 涛 付 欣
(海军驻昆明750军代室1) 昆明 650051)(海军工程大学兵器工程系2) 武汉 430033)(92858部队3) 宁波 315812)
1 引言
捷联式惯性导航系统将陀螺和加速度计等惯性传感器与载体固连,用计算机来完成导航平台功能,相比平台式惯导系统具有两个显著的特点:1)惯性仪表便于安装和维护,也便于更换;2)惯性仪表可以直接给出航行器线加速度和角速度信息,而这些信息是航行器控制系统所需要的。此外,捷联式惯导还具有功能强、重量轻、成本低等优点,因而逐渐成为主流的惯性导航方式,特别是在体积受限的水下航行器中得到了广泛应用。
由于惯性导航系统造价昂贵、结构复杂、加之捷联惯导水下试验难度高、花费大,所以借助系统仿真开发出一种水下航行器捷联惯性导航仿真系统,以模拟真实惯导,并依此研究影响捷联惯导精度的因素和提高导航精度的方法,以减少研制经费,降低研制难度。近年来,很多学者利用各种软件对捷联惯导仿真进行了广泛深入研究[1~3],但这些研究重点都集中于如何用软件实现导航仿真模块和惯性元件模块,忽视了载体轨迹模块的设计,所以无法提供实验对比的基准,限制了影响导航精度各因素的进一步研究。虽然很多文献详细讨论了载体运动轨迹[4~5],但其复杂程度让人望而生畏,如果根据航行器模型和力学原理,用数学方法来产生一个与实际完全相符的航行轨迹数据,将会因为各航行轨迹量之间的耦合关系,使数学模型的建立非常复杂。本文在系统阐述了捷联惯导仿真系统功能模块基础上,详细阐述一种简单易实现的航行轨迹数据产生方法,使整个仿真系统更完备,为后续研究仿真精度奠定基础。
2 仿真系统模型
系统仿真是以实际系统为原型,根据实际系统的某些属性,关系和功能,建立与原型相似的模型。通过仿真实验,可以加深对原系统的认识,从而为原系统的改进提供指导性的技术支持。
进行捷联惯导算法仿真研究,需要陀螺仪和加速度计的测量数据以及航行器的真实轨迹数据,可先通过模拟出一条航行器的航迹,计算陀螺仪和加速度计的输出,作为仿真的输入,仿真结果和模拟出的航行器航迹数据相比较,得到误差曲线,检验仿真的正确性。捷联惯导仿真系统原理如图1所示。
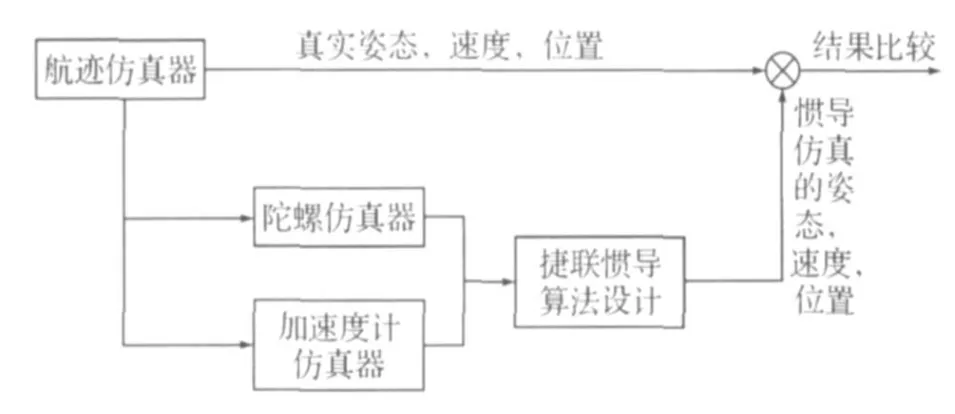
图1 捷联惯导仿真系统原理图
3 航迹仿真器设计
航迹仿真器的作用就是生成航行轨迹数据,它是测试验证导航仿真系统而必需的输入信号源;对于捷联式惯导仿真系统,需要诸如:姿态角(航向角、俯仰角、倾斜角)、位置(纬度、经度、深度)、速度(相对地球系的北向速度、东向速度、地向速度)以及陀螺和加速度计的理想输出数据等共十五个数据。
根据运动学观点,一般刚体运动可以拆分为两个子运动:定点转动和平移,其中转动完全独立于平移[6]。
对于捷联惯导仿真系统测试验证所用航行轨迹数据,我们用如下方法得到,假设航行体的某一段运动轨迹,该轨迹用两组独立的方程组描述:相互独立的三个姿态角时间函数和三个位置时间函数;这样做出的航行轨迹虽然不完全是实际航行轨迹,但是可以很方便地得到任意时刻的精确测试用航行轨迹数据,用来验证导航仿真系统的正确性和精度。航行数据的生成方法和具体公式如下:
3.1 航行姿态数据生成方法
航行姿态数据包括航行器任意时刻的姿态角数据和载体系相对于导航系的转动角速度数据。可先设定姿态角随时间变化的函数,由此可以得到姿态角一阶导数随时间变化的函数,再由姿态角和姿态角的一阶导数算出载体系相对于地理系的转动角速率在载体系中的投影。
1)姿态角及其一阶导数的变化规律
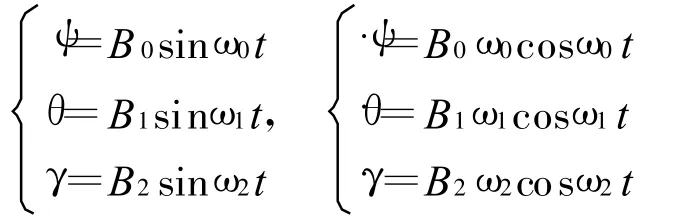
2)载体系相对于导航系的转动角速率在载体系中的投影[7]
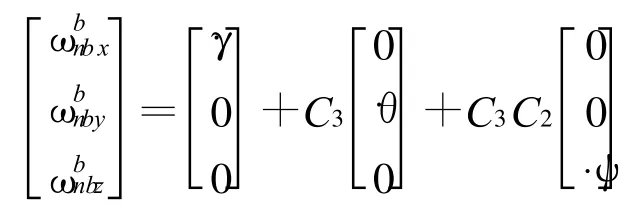
其中
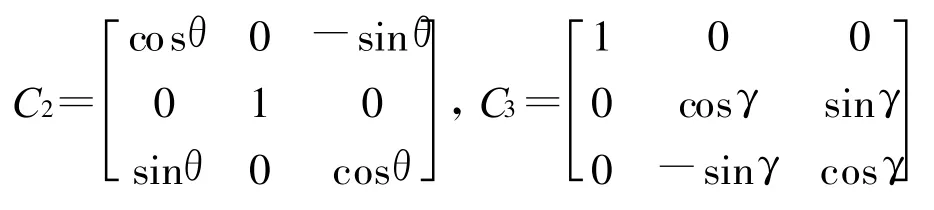
3.2 航迹数据生成方法
航迹数据包括航行器任意时刻速度和位置数据以及导航系中地速变化率数据。推导航迹数据时,将航行体看作一个运动着的质点,其航迹的变化与航行姿态的变化无关。
先设定位置(纬度、经度、深度)随时间变化的函数,并计算位置的一阶、二阶导数。再计算地球直角坐标系中,纬度、经度、深度对应的直角坐标值R(x,y,z),并求直角坐标的一阶导数R′、二阶导数R″。R′就是相对于地球的速度在地球系中的投影与地球系向导航系的坐标转换矩阵叉乘就得到航行轨迹数据中的速度数据。R″是在地球系中的对地加速度在地球系中的投影,R″乘上就得到在地球系中的对地加速度在导航系中的投影。航行轨迹中的加速度数据是导航系中的对地加速度在导航系中的投影an,由哥氏转动定理,an和之间相差一个载体相对于地球转动所产生的向心加速度ωe n×。
1)设定位置的变化规律为时间的正弦函数,并计算位置的一阶、二阶导数
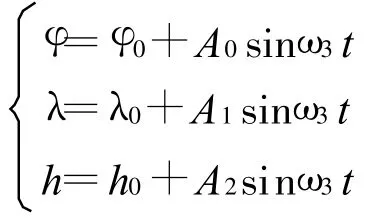
2)求解位置在地球系下的坐标值(x,y,z),并计算其一阶层数(x′,y′,z′)、二阶导数(x″,y″,z″)(具体公式略)
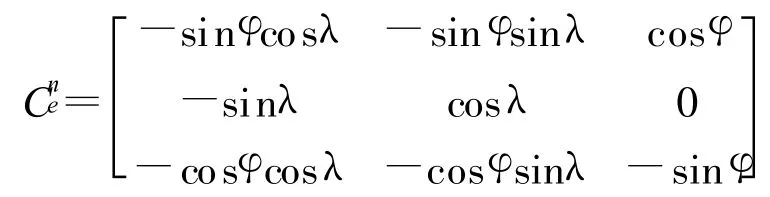
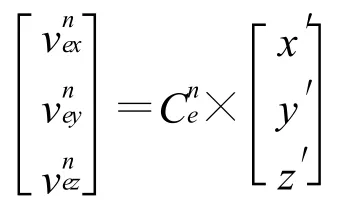
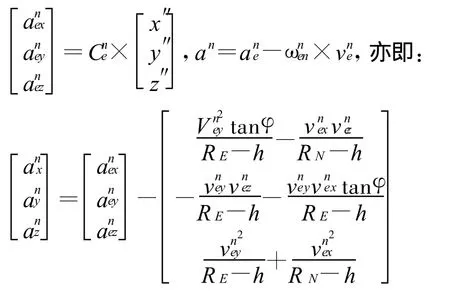
4 陀螺及加速度计数学模型
1)陀螺数学模型
完整的陀螺模型包括理想输出量、随机误差量(随机常值误差、白噪声、一阶马尔可夫过程误差)、刻度因子误差。用数学公式表示如下:
式中:UG为完整陀螺模型的输出,KG为刻度因子,δ KG为刻度因子误差,DG0为陀螺随机常数误差,DG 1为陀螺白噪声误差,DG 2为陀螺一阶马尔可夫过程误差,为陀螺模型理想输出:
2)加速度计数学模型
与陀螺模型相同,完整的加速度计模型包括理想输出量、随机误差量、刻度因子误差。用数学公式表示如下:
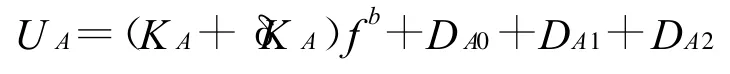
式中:UA为完整陀螺模型的输出,KA为刻度因子,δ KA为刻度因子误差,DA0为加速度计随机常数误差,DA1为加速度计白噪声误差,DA2为加速度计一阶马尔可夫过程误差,fb为陀螺模型理想输出:¯fb
5 仿真实验及结论
按照前述仿真系统模型,利用Matlab 7软件,采用如下捷联惯导算法进行仿真实验:姿态解算采用等效旋转矢量三子样优化算法,导航解算采用三子样划桨补偿优化算法[9~11];
仿真参数选择如下:仿真时间t=1800s,采样时间:ts=0.01s,子样数:n=3;φ0=30°,λ0=100°,h0=300m,A0=1.5°,A1=1.5°,A2=1000m,B0=B1=B2=15°,ω0=ω1=ω2=2π/240,ω3=2π/(7200*40)。
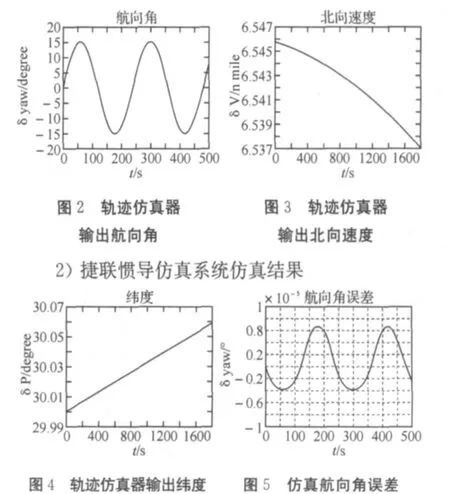
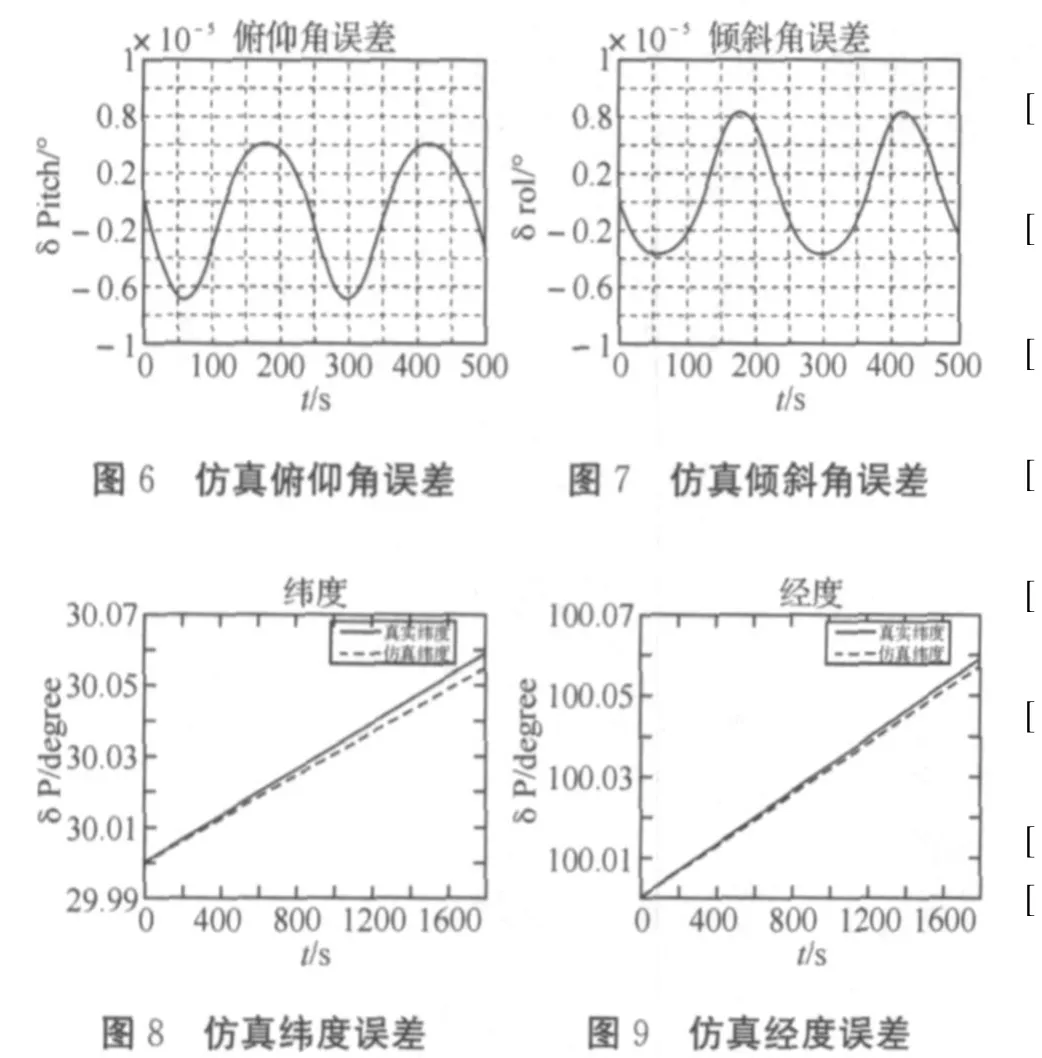
理想对准精度,理想惯性条件下仿真结果如图2~9所示(篇幅所限,轨迹仿真器仅给出3幅仿真图),由图2~4可见,建立的轨迹仿真器能方便的生成任意时刻所需的真实导航参数,给惯导仿真系统提供了基准,便于仿真研究、提高捷联惯导精度;图5~9所示为将轨迹仿真器输出数据与捷联惯导仿真数据进行对比得到误差的仿真图,由图可见纯惯导系统的导航误差随时间积累,符合检验标准,这也验证了本文轨迹仿真器数据的合理性及仿真系统参数解算的正确性。
1)轨迹仿真器仿真结果
[1]王海青.惯性导航系统仿真试验研究[J].飞机设计,2007(10):43~48
[2]蓝仁恩,付战平.基于Matlab_Simulink的捷联惯性导航仿真研究[J].计算机仿真,2007(11):45~46
[3]赵方,李永红.基于Simulink/S-Function的惯性导航系统的仿真[J].四川兵工学报,2008(2):86~89
[4]郑亚弟.导航载体轨迹仿真系统的研究与开发[D].解放军信息工程大学硕士论文,2006
[5]张婷.轨迹仿真器设计[J].微计算机信息,2008(4):241~242
[6]J.M.McCarthy.Introduction to Theoretical kinematics:MIT Press,Cambridge,Massachusetts,1990
[7]张天光,王秀萍,王丽霞,等译.捷联惯性导航技术[M].第二版.北京:国防工业出版社,2007:24~32
[8]陆元九.陀螺及惯性导航原理上册[J].北京:科学出版社,1964
[9] 秦永元.惯性导航[M].北京:科学出版社,2007:288~340
[10]P.G.Savage.Strapdown inertial navigation integration algorithm design,part 1:attitude algorithms[J].Journal of Guidance,Controland Dynamics,1998,21(1):19~28
[11]P.G.Savage.Strapdown inertial navigation integration algorithm design,part 2:velocity and position algorithms[J].Journal of Guidance,Control and Dynamics,1998,21(2):208~221

