极限上限分析中“切线法”引入非线性破坏准则的探讨
赵炼恒,李 亮,但汉成,罗苏平,任东亚
(中南大学土木建筑学院,长沙 410075)
极限上限分析中“切线法”引入非线性破坏准则的探讨
赵炼恒,李 亮,但汉成,罗苏平,任东亚
(中南大学土木建筑学院,长沙 410075)
基于极限分析上限法,讨论了“切线法”引入非线性M-C破坏准则时采用“初始切线法”和“外切线法”对边坡临界高度、地基承载力、主动土压力3个经典土力学问题的影响,用以分析“外切线法”引入非线性破坏准则对分析岩土问题的合理性和有效性。研究表明:非线性参数对土工结构的安全性有重要影响,恰当引入岩土材料的非线性破坏特性更加符合工程实际;基于上限法通过“初始切线法”引入非线性破坏准则是众多上限解答的一个上限解答,特定条件下能够获得较好的上限解,但随着非线性参数m的增大由此引起的误差也越来越大,采用“外切线法”更具有效性和合理性。
土力学;非线性M-C破坏准则;极限上限法;切线法
1 概 述
现有研究表明,岩土介质服从非线性破坏准则[1-4],自从Zhang和Chen(1987)[5]引入了幂函数非线性破坏准则以来,基于该破坏准则的岩土工程问题的分析研究成为热点。Collins(1988)[6],Drescher(1988)[7]和马崇武(1999)[8]根据“插值法”,采用非线性破坏准则获得了边坡的稳定性系数。Maksimovic(1996)[9]和Li(2007)[10]结合数值分析法分析了岩土非线性破坏准则对边坡稳定性的影响。王建锋(2005)[11]基于Janbu普遍条分法,获得了非线性强度下的边坡稳定性分析;胡卫东(2006)[12]基于极限平衡法研究了非线性强度准则对边坡安全系数的影响。
上限法由于其明确的物理意义和能够提供严格的解答范围而被更多学者认可,杨小礼(2002,2004,2006,2007)[13-16]基于非线性SQP优化方法和“外切线法”研究了边坡的稳定性,土压力和地基承载力问题。胡卫东(2007)[17]采用“初始切线法”对螺旋线破坏机制条件下的竖直边坡进行了稳定性系数计算并与Zhang X J和Chen W F(1987)[5]的结果进行了对比,认为“初始切线法”引入非线性破坏准则的方法也是有效、合理的。但由于该文献所举对比算例极为有限,尚不足以说明“初始切线法”的正确性,此时ct和φt实际均为常数,在进行分析时与基于线性破坏准则的方法无实质上的差别,因而“初始切线法”的合理性有待进一步证实。
基于以上原因,本文主要讨论“外切线法”引入非线性破坏准则时采用“初始切线法”和“外切线法”对边坡临界高度、地基承载力、主动土压力3个经典的土力学问题的影响,用以分析“外切线法”引入非线性破坏准则对岩土问题的合理性和有效性。
2 基本理论与假设
2.1 非线性破坏准则
设非线性破坏准则为

将式(1)绘制成如图1所示的曲线。c0,σt,m均为需通过试验确定的岩土材料参数,c0为曲线与纵轴的截距,-σt为曲线与横轴的截距,曲线恒定通过(0,c0)和(-σt,0)两点,m决定强度曲线的弯曲程度,进而影响岩土材料的屈服特性。当m=1时,式(1)变为线性Mohr-Coulomb强度准则。
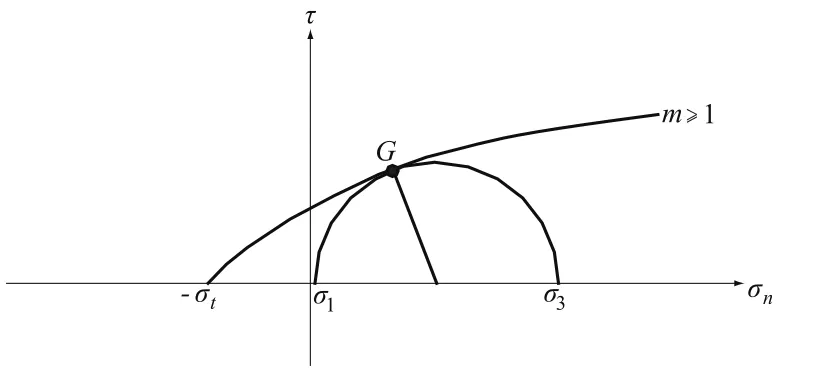
图1 非线性破坏准则Fig.1 Nonlinear failure criterion curve
2.2 基于非线性破坏准则的极限分析方法
结构上限分析时,提高材料的屈服强度不会降低结构的极限载荷,因而采用上限分析时,对非线性破坏准则下的上限分析可采用“外切线法”,以提高岩土材料强度为手段来分析结构物的上限解[2,18]。2.2.1 外切线法
图2中虚线所示即为由切线和初始切线确定的线性破坏准则,切线为经过非线性破坏准则上的任一点并与其外切的直线方程,若曲线的曲率随着σn的增加而减小则切线完全位于曲线的外侧,位于直线破坏准则上的所有点对应的材料强度均相应得到了提高,故切线表示的破坏准则上限解答一定为真实解答的上限。初始切线属于切线的一种特殊情况,切点位于点(σn=0,τ=c0)处,一般情况下该初始切线表示的破坏准则大于切线表示的破坏准则,因而也是真实解答的一个上限。

图2 非线性破坏准则的切线Fig.2 The tangential line for a nonlinear failure criterion
表达式(1)的切线方程为
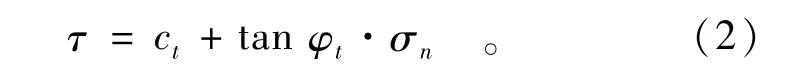
式(2)中,ct,tanφt分别表示切线的截距和斜率,如图1所示。ct,tanφt的表达式为

2.2.2 初始切线法
当采用“初始切线法”时,由于切点位于点(σn=0,τ=c0)处将σn=0代入式(4),可得初始切线的斜率
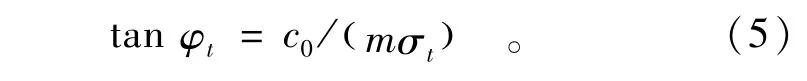

则初始切线的方程为c0和φt一经确定后,ct,tanφt实际退化为只与非线性参数m相关的参数了,此时即可用初始切线代替非线性破坏曲线做上限分析,在进行上限分析时与线性破坏准则便无差别。
2.2.3 基本假设
基于岩土材料非线性破坏准则,本文在采用极限分析上限理论对“外切线法”引入非线性破坏准则时,应用了如下假设:①所有问题均符合平面应变问题条件;②岩土材料为理想刚塑性体,破坏时服从非线性M-C破坏准则,破坏面上某一点对应的抗剪强度指标为ct,φt(ct,φt的具体含义如图2所示),并遵循相关联流动法则。
需要说明的是:极限分析上限定理是对服从相关联流动准则的材料而发展起来的,因而对满足非相关联流动准则的岩土材料是不适用的,然而根据极限分析定理[18]:服从非相关联流动准则的材料的实际破坏荷载,必定小于或等于服从相关联流动准则的同样材料的实际破坏荷载。因而采用相关联流动准则计算土工构筑物的极限平衡状态参数实际仍然满足上限定理的基本概念。
3 对比计算与分析
为分析“外切线法”引入非线性破坏准则进行上限分析的合理性和有效性,选取了以下3个经典的土力学问题进行计算与分析。
3.1 边坡临界高度、稳定性系数
3.1.1 对数螺旋线破坏机制
已有研究成果表明[2,5,17,18]:简单边坡的破坏面更接近对数螺旋面形状,因而在简单边坡上限分析中也较常采用这种旋转破坏机构。以对数螺旋线旋转间断机构为例进行分析,如图3所示。根据上限法能耗计算过程,使外荷载所做的功率等于内能耗散率,可求得边坡稳定性系数Ns(θh,θ0,α,β、β′,φt):

图3 边坡稳定性的破坏机构Fig.3 Rotational failuremechanism for slope stability

式中:f1,f2,f3,f4为与θh,θ0,α,β,β′,φt相关的函数,具体表达式同文献[18],不同在于本文中的内摩擦角采用“外切线法”引入的基于非线性破坏准则的内摩擦角φt。
进而可以获得边坡的临界高度Hcr:

3.1.2 问题的分析
根据极限分析上限定理,上式给出了边坡稳定性系数Ns的一个上限。当θh,θ0,β′,φt满足条件:

时,函数Ns(θh,θ0,α,β,β′,φt)取得一个最小值,进而得到边坡临界高度Hcr的一个最小上限。以上最小值求解过程可以采用序列二次规划优化方法实现。值得注意的是:上述分析中采用“初始切线法”和“外切线法”时ct和φt的取值是不同的。对于“初始切线法”,ct和φt实际已经转化为常量;而对于“外切线法”,ct和φt为变量参与了优化计算过程。
3.1.3 对比计算与分析
为便于分析,选取文献[5]的算例为研究对象,假设边坡岩土材料服从非线性破坏准则,坡顶倾角α=0°,坡趾倾角β分别为45°,60°,75°,90°,土的重度γ=18.6 kN/m3,岩土体粘结力c0=90 kN/m2,σt=247.3 kN/m2,当m=1.0,1.2,1.4,1.6,1.8,2.0,2.5时稳定性系数Ns计算对比的结果如表1和图4所示。
由表1和图4可知:随着m的增大,稳定性系数Ns下降得较快,因而岩土体非线性强度参数的取值对评定土坡稳定性有着重要的影响,同时对于岩土材料,引入非线性强度曲线假设是非常必要的,因为非线性破坏准则更符合工程的实际情况。
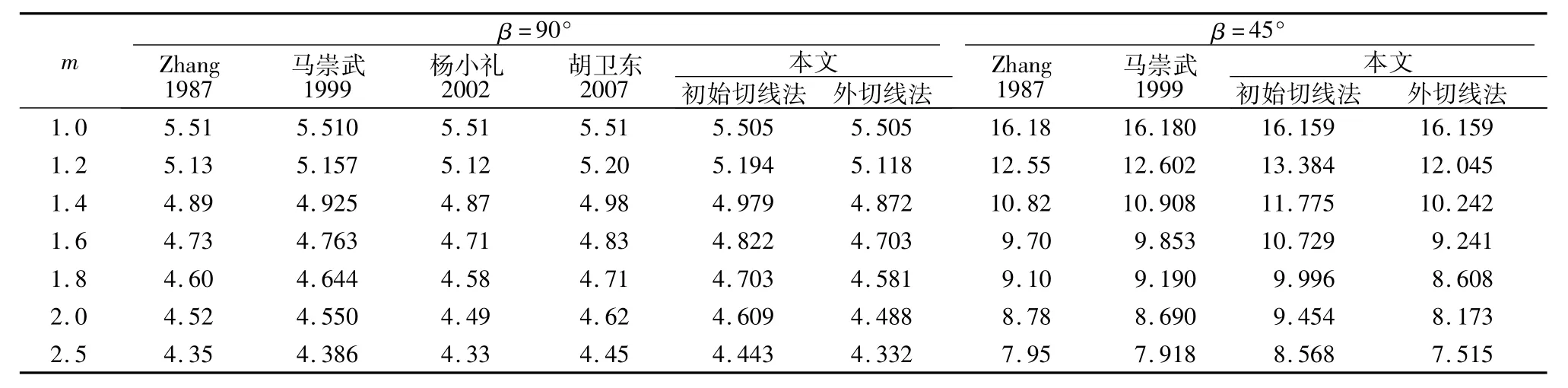
表1 非线性破坏准则下边坡稳定性系数Ns计算结果对比Table1 Comparison of results obtained by differentmethods on slope stability factor Nsbased on nonlinear failure criterion
非线性破坏准则条件和其它参数不变的情况下,随着边坡坡趾倾角β的减小,采用“初始切线法”获得的结果与较优的上限解答结果误差增大,由β=90°时的最大绝对误差2.95%增加至β=45°时的最大绝对误差16.12%。可见:对于边坡倾角较大的情况,采用“初始切线法”引入非线性破坏准则的方法误差较小;但对于边坡倾角较小的情况,采用“初始切线法”引入非线性破坏准则的方法会造成较大的误差。同时,对比表明,本文采用“外切线法”引入非线性破坏准则所获得的计算结果是同类方法中的较小结果,故对于上限法而言可以认为本文结果更接近于真实解答,是更优解答。
3.2 挡土墙主动土压力
3.2.1 对数螺旋线破坏机制

式中:f1,f2,f3,f4,f5,f6,f7为与θh,θ0,β,φt相关的函数,具体表达式同文献[16,18],其中能量耗散计算参数c和φ为采用“外切线法”引入的基于非线性破坏准则的粘聚力ct和内摩擦角φt。
3.2.2 问题的分析
根据极限分析上限定理,上式给出了主动土压力Pa的一个下限。当θh,θ0,φt满足条件

时,函数Pa(θh,θ0,β,φt)取得一个最大值。以上最大值求解过程可以采用序列二次规划优化方法实现。同样需要注意的是:上述分析中采用“初始切线法”和“外切线法”时ct和φt的取值是不同的。对于“初始切线法”,ct和φt实际已经转化为常量;而对于“外切线法”,ct和φt为变量参与了优化计算过程。
3.2.3 对比计算与分析
为便于分析,选取文献[16]的算例为研究对象,假设边坡岩土材料服从非线性破坏准则,墙后填土水平,墙趾倾角β为90°,土的重度γ=18 kN/m3,岩土体粘结力c0=9 kN/m2,σt=20 kN/m2,当m=1.2,1.4,1.6,1.8,2.0时主动土压力Pa计算对比的结果如图6所示。
由图6可知:随着m的增大,主动土压力Pa明显增大,因而岩土体非线性强度参数的取值对评定土坡稳定性有着重要的影响,对于岩土材料,引入非线性强度曲线假设是非常必要的,因为非线性破坏准则更符合工程的实际情况。非线性破坏准则条件和其它参数不变的情况下,随着非线性参数m的增大,采用“初始切线法”获得的结果与较优的上限解答结果误差增大,由m=1.2时的最大绝对误差7.73%增加至m=2.0时的最大绝对误差13.28%。可见:对于非线性程度较大的情况,采用“初始切线法”引入非线性破坏准则的方法会造成较大的误差,采用“外切线法”引入非线性破坏准则的方法具有更好的合理性。

图4 非线性破坏准则下边坡稳定性系数Ns计算结果对比Fig.4 Comparison of calculated results obtained from differentmethods of slope stability factor Nsbased on nonlinear failure criterion
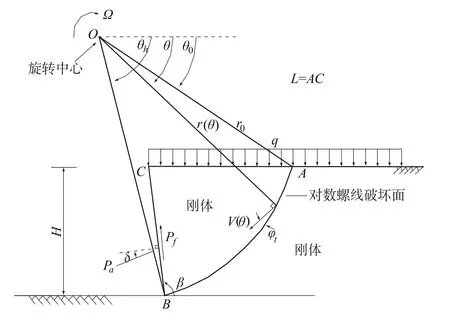
图5 主动土压力计算的破坏机制Fig.5 Logarithm ic spiral failuremechanism for active earth pressure

图6 非线性破坏准则下主动土压力计算结果对比Fig.6 Com parison of calculated results obtained from differentmethods of active earth pressure based on nonlinear failure criterion
3.3 条形基础Prandtl机制地基承载力
3.3.1 Prandtl破坏机制
引用文献[18]的粗糙条形基础地基承载力Prandtl破坏机制如图7。根据上限法能耗计算过程,使外荷载所做的功率等于内能耗散率,可求得粗糙条形基础地基极限承载力Pu(ξ,η,φt):

图7 粗糙条形基础破坏机制Fig.7 Failuremechanism for ultim ate bearing capacity of rough strip foundation

具体推导过程见文献[18],其中能量耗散计算参数c和φ为采用“外切线法”引入的基于非线性破坏准则的粘聚力ct和内摩擦角φt。
3.3.2 问题的分析
根据极限分析上限定理,上式给出了极限承载力Pu的一个上限,通过换算可求得相应的承载力系数Nc和Nq。当ξ,η,φt满足条件:

时,函数Pu(ξ,η,φt)取得一个最小值。以上最小值求解过程可以采用序列二次规划优化方法实现。同样值得注意的是:上述分析中采用“初始切线法”和“外切线法”时ct和φt的取值是不同的。对于“初始切线法”,ct和φt实际已经转化为常量;而对于“外切线法”,ct和φt为变量参与了优化计算过程。
3.3.3 对比计算与分析
为便于分析,选取文献[13]的算例为研究对象,假设基础下岩土材料服从非线性破坏准则,土体无重度γ=0 kN/m3,基础两侧地表超载q=57 kN/m2,岩土体粘结力c0=90 kN/m2,σt=247.3 kN/m2,当m=1.0,1.2,1.4,1.6,1.8,2.0,2.5时极限承载力Pu计算对比的结果如表2和图8所示。
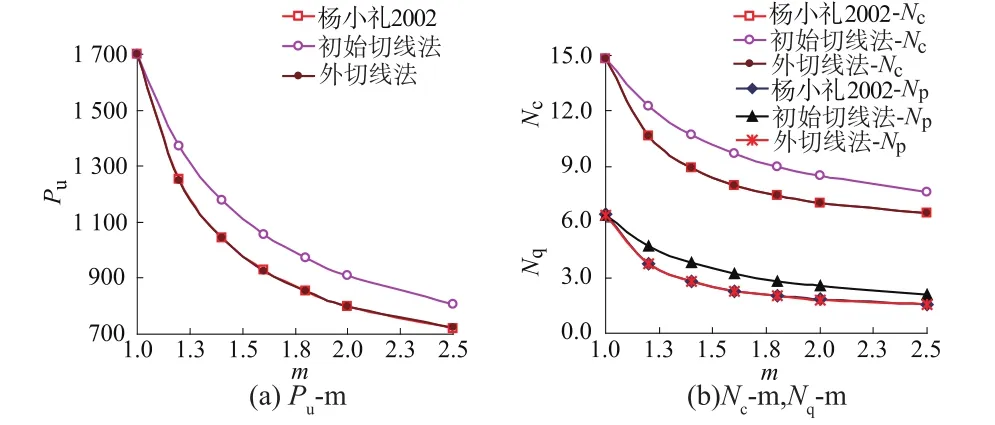
图8 非线性破坏准则下极限承载力Pu和承载力系数Nc和Nq计算结果对比Fig.8 Com parison of calculated results obtained from differentmethods of ultimate bearing capacity and bearing capacity coefficients based on nonlinear failure criterion
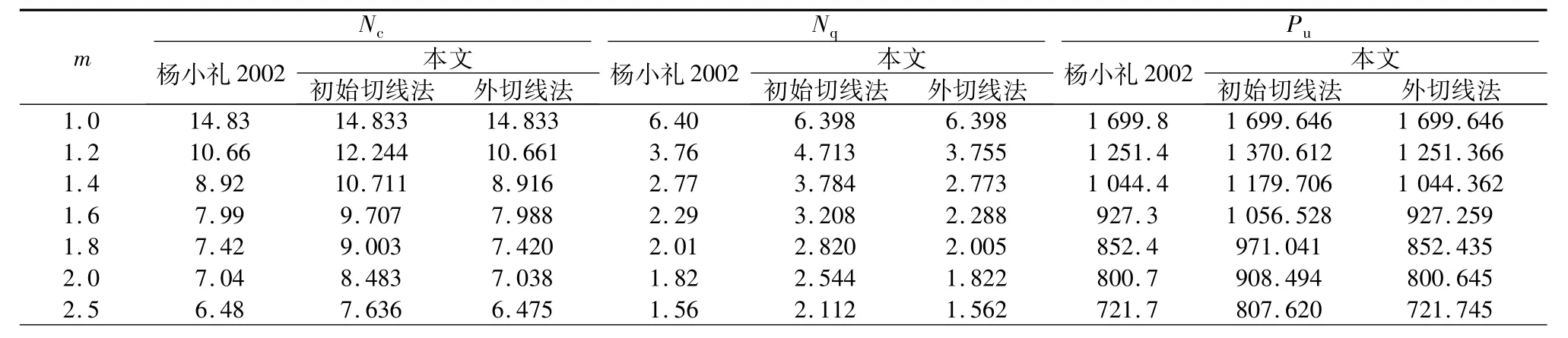
表2 非线性破坏准则下地基极限承载力计算结果对比Table2 Comparison of calculated results obtained from differentmethods of ultimate bearing capacity based on nonlinear failure criterion
由表2和图8可知:随着m的增大,极限承载力Pu减小得较快,因而岩土体非线性强度参数的取值对评定地基承载力有着重要的影响,对于岩土材料,引入非线性强度曲线假设是非常必要的,因为非线性破坏准则更符合工程的实际情况。非线性破坏准则条件和其它参数不变的情况下同样可见:对于非线性程度较大的情况,采用“初始切线法”引入非线性破坏准则的方法会造成计算结果的较大误差,采用“外切线法”引入非线性破坏准则的方法具有更好的合理性。
4 结 论
基于极限分析上限法,本文讨论了“外切线法”引入非线性破坏准则时采用“初始切线法”和“外切线法”对3个经典土力学问题的影响,研究表明:
非线性破坏准则符合岩土材料的实际情况。较现有线性破坏准则而言,岩土体非线性强度参数m的值越大,岩土体构筑物的安全性越差,因而引入岩土体非线性强度准则对确保土工结构物的可靠性有着重要意义,工程实际中有必要通过“外切线法”引入非线性破坏准则进行土工结构安全性评价。
基于上限法通过“初始切线法”引入非线性破坏准则是众多上限解答的一个,特定条件下能够获得较好的上限解,但随着非线性参数的增加由此引起的误差也越来越大。对于非线性程度较强的情况,采用“初始切线法”引入非线性破坏准则的方法会造成计算结果的较大误差,采用“外切线法”具有更加明显的有效性和合理性。
[1] CHARLES JA.Correlation between laboratory behaviour of rockfill and field performance with particular reference to Scammonden Dam[D].London:University of London,1973.
[2] CHENW F,LIU X L.Limit Analysis in Soil Mechanics[M].Amsterdam:Elsevier Science,1990.
[3] HOEK E,BROWN E T.Practical estimate the rock mass strength[J].International Journal of Rock Mechanics andMining Sciences,1997,34(8):1165-1186.
[4] BAKER R.Nonlinear Mohr Envelopes based on triaxial data[J].Journal of Geotechnical and Geoenvironmental Engineering,ASCE,2004,130(5):498-506.
[5] ZHANG X J,CHEN W F.Stability analysis of slopes with general nonlinear failure criterion[J].International Journal for Numerical and Analytical Methods in Geomechanics,1987,11(1):33-50.
[6] COLLINS IF,GUNN C IM,PENDERM J,etal.Slope stability analysis for materials with a non-linear failure envelope[J].Int.I.Num.Analyt.Meth.Geomech.,1988,12(6):533-550.
[7] DRESCHER A.,CHRISTOPOULOS C.Limit analysis slope stability with nonlinear yield condition[J].International Journal for Numerical and Analytical Methods in Geomechanics,1988,12(3):341-345.
[8] 马崇武,武生智,苗天德.对非线性破坏准则下边坡稳定性分析的线性简化[J].兰州大学学报(自然科学版),1999,35(1):49-52.(MA Chong-wu,WU Sheng-zhi,MIAO Tian-de.Linearization on slope stability analysiswith nonlinear fallure criterion[J].Journal of Lanzhou University(Natural Sciences),1999,35(1):49-52.(in Chinese))
[9] MAKSIMOVICM.A family of nonlinear failure envelopes for non-cemented soils and rock discontinuities[J].The Electronic Journal of Geotechnical Engineering,1996(1):1-62.
[10]LI X.Finite element analysis of slope stability using a nonlinear failure criterion[J].Computers and Geotechnics,2007,34(3):127-146.
[11]王建锋.非线性强度下的边坡稳定性[J].岩石力学与工程学报,2005,24(supp.2):5897-5900.(WANG Jian-feng.Slope stability analysiswith nonlinear failure envelopes[J].Chinese Journal of Rock Mechanics and Engineering,2005,24(supp.2):5897-5900.(in Chinese))
[12]胡卫东,祝新念,李小强.非线性破坏准则下的边坡稳定分析[J].湖南理工学院学报(自然科学版),2006,19(3):85-91.(HU Wei-dong,ZHU Xin-nian,LIXiao-qiang.Slope stability analysiswith nonlinear failure criterion[J].Journal of Hunan Institute of Science and Technology(Natural Sciences),2006,19(3):85-91.(in Chinese))
[13]杨小礼.线性与非线性破坏准则下岩土极限分析方法及其应用[D].长沙:中南大学,2002.(YANG Xiaoli.Limitanalysismethod and its application to geotechnical engineering with linear and nonlinear failure criteria[D].Changsha:Central South University,2002.(in Chinese))
[14]YANG Xiao-li,YIN Jian-hua.Slope stability analysis with nonlinear failure criterion[J].Journal of Engineering Mechanics,ASCE,2004,130(3):267-273.
[15]YANG Xiao-li,YIN Jian-hua.Estimation of seismic passive earth pressure with non-linear failure criterion[J].Engineering Structures,2006,28(3):342-348.
[16]YANG Xiao-li.Upper bound limitanalysis of active earth pressure with different fracture surface and nonlinear yield criterion[J].Journal of Theoretical and Applied Fracture Mechanics,2007,47(1):46-56.
[17]胡卫东,张国祥.非线性破坏准则下的边坡稳定塑性极限分析[J].岩土力学,2007,28(9):1909-1913.(HUWei-dong,ZHANG Guo-xiang.Plastic limit analysis of slope stability with nonlinear failure criterion[J].Rock and Soil Mechanics,2007,28(9):1909-1913.(in Chinese))
[18]CHENW F.Limit Analysis and Soil Plasticity[M].Amsterdam:Elsevier,1975.
(编辑:赵卫兵)
Discussion on Generalized Tangential M ethod Led in Nonlinear Failure Criterion in Upper Boundary Lim it Analysis
ZHAO Lian-heng,LILiang,DAN Han-cheng,LUO Su-ping,REN Dong-ya
(College of Civil and Architectural Engineering,Central South University,Changsha 410075,China)
On the basis of the upper boundary limit analysis theorem and nonlinear M-C failure criterion,three classical soilmechanics problems including the ultimate bearing capacity of a rough strip foundation,the critical height of a slope and the active soil pressure were studied bymeans of generalized tangential technique and the kinematic approach of limit analysis theory.The rationality and feasibility of the generalized tangentialmethod and the inceptive tangentialmethod were analyzed.From the numerical results,it can be seen that the nonlinear failure parameter exerts a significant effect on the safety of the geotechnical structure,and leading-in a proper nonlinear failure character of geo-materialsmore agreeswith the engineering practice.The case study and comparative analysis show that a better solution could be achieved bymeans of the inceptive tangentialmethod under specific conditions,but the larger the nonlinear coefficient is,the bigger the deviation caused by the inceptive tangentialmethod is.The generalized tangentialmethod possesses the rationality and feasibility obviously.
soilmechanics;nonlinear M-C failure criterion;upper-boundary theorem of limit analysis;generalized tangentialmethod
TU432
A
文献[16]的主动土压力对数螺旋线破坏机制如图5。根据上限法能耗计算过程,使外荷载所做的功率等于内能耗散率,可求得边坡稳定性系数Pa(θh,θ0,β,φt):
1001-5485(2010)08-0034-06
2009-09-15;
2009-12-04
西部交通建设科技项目(2006318802111);中南大学优秀博士学位论文扶植项目(2008yb004);铁道部科技研究开发计划重点资助项目(2008G032-3);湖南省交通厅科技项目(2007-29)
赵炼恒(1980-),男,湖南益阳人,讲师,博士,主要从事道路与铁道工程、地基处理等方面的研究工作,(电话)13755139425(电子信箱)zlh8076@163.com。

