多阶自适应算术编码研究

李 彬，倪桂强，罗健欣

(解放军理工大学 指挥自动化学院，江苏 南京210007)

数据压缩分为有损压缩和无损压缩。其中无损压缩编码是基于信息熵原理的可逆编码，目前主要有基于统计模型的哈夫曼编码和算术编码，以及基于字典模型的LZ系列编码。算术编码克服了哈夫曼编码只能用整数位的代码表示一个信源符号的缺点，而采用了用一个浮点数表示一个信源符号流的思想，可以更逼近信源编码。算术编码算法在静止图像压缩编码标准JPEG2000[1]和视频编码标准H.264[2]中已被作为国际标准广泛采用。

提高编码的压缩率和降低编码的时间、空间复杂度是人们研究压缩编码算法的主要目的。基于对信息中单个符号频率统计的算术编码是一种向极限挑战的编码方式。本文研究的多阶自适应算术编码着重通过研究符号在某符号序列之后出现的概率来获得高效压缩。参考文献[3]介绍了一种基于多阶上下文自适应的二进制算术编码的实现，实现了3阶自适应。参考文献[4]介绍了一种能降低复杂度和内存空间但是略微降低了编码效率的简化编码模型。本文的多阶自适应算术编码对参数进行了优化，可以进行更高阶次的编码（测试中最高可达11阶），在最大限度降低空间消耗的同时，获得更好的压缩效果。与LZW和WinRAR的性能比较结果表明，本文的多阶自适应算术编码能获得更满意的压缩效果。

1 算术编码

1.1 算术编码原理

算术编码将被编码的信源符号流表示成实数半开区间[0，1)中的一个数值间隔，这个间隔随着信息流中每一个信源符号的加入逐步减小，每次减小的程度取决于当前加入的信源符号的概率。概率高者减少的程度低，概率低者减少的程度高。符号流越长，代表它的间隔越小，编码表示这一间隔所需的位数就越多。从算术编码过程中产生的数值可以被唯一地解码，精确地恢复原始的信源符号流[3]。

设信源符号集由 3个信源符号{a1，a2，a3}组成，根据已知的信源符号概率，在[0，1)区间上为它们分配相应的子区间，子区间大小与概率成正比。其概率分布及对应的子区间如表1所示。

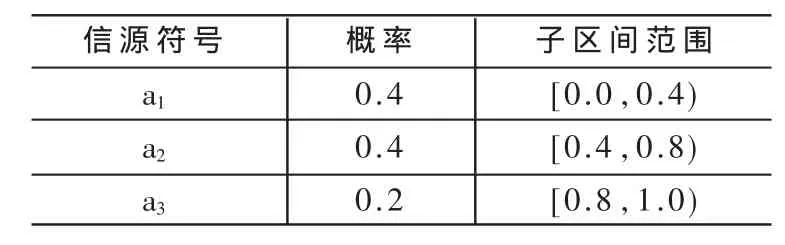
表1 信源符号及其数值范围

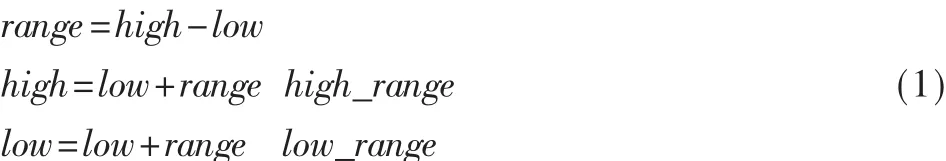
用range表示编码输出数值落入的间隔，high为range的上界，low为下界，初始时 high为 1，low为 0。 用high_range表示某符号子区间的上界，low_range为下界。每一信源符号被编码后，根据公式(1)计算 high、low及range的新值，并根据概率分布重新划分被编码符号的子区间。最后一个符号得到的间隔内的任何一个实数代表整个符号流。对符号流“a1a2a3a2a1”进行算术编码的过程如图1所示，用0.305就可以唯一地代表这个符号流。

1.2 多阶自适应算术编码

根据编码过程中信源符号是否更新概率分布，算术编码分为静态模型和自适应模型。静态模型的缺点是：首先需要在编码前对信源符号的分布进行统计，会消耗大量时间；其次符号的概率是该符号在整个信息中的概率，根据信息熵原理，不利于对信息的压缩。而自适应模型随着符号的读入，实时动态更新符号的概率分布，能统计出某个符号在局部的出现概率或某个符号相对于某一上下文的出现概率，压缩效果好于静态模型。

自适应编码中，初始时假设各个符号的概率相同，并平均分配区间[0，1)，随着符号的读入，相应地更新其概率值，与之对应的子区间亦随之改变。若有新的符号出现则加入符号集即可。仍设信源符号集由3个符号{a1，a2，a3}组成，对于符号流“a1a2a3a2a1”，各个符号概率更新、子区间比例变化、符号累计及间隔变化过程如表2所示。

最后一个符号输入后不再划分子区间，得到读入a1后的区间[0.238 9，0.240 4)，即编码结果的输出数值区间，如0.24就可以作为符号流编码结果。同样类似的解码过程可以唯一地解出原符号流。

如果编码时考虑符号之间的相关性，把多个符号按照不同的上下文结构组合在一起，当作一个编码单元进行自适应算术编码，就可以进一步提高编码效率。用“阶”表示上下文相关符号序列的长度，那么1阶上下文自适应统计的就是符号在某个特定的符号后面出现的概率，同样2阶、3阶上下文自适应统计的是符号在某两个、三个特定符号后面出现的概率。使用多阶算术编码，使得同一符号可以在多个动态统计的上下文概率表中取得概率值较大的进行编码，从而使总熵值更小。如在1阶自适应编码中，在已经编码的10 000个符号后，刚刚编码的符号是a1，下一个要编码的符号是a2，在之前的10 000个符号中统计到出现了100个a1和 a2，a2出现在 a1之后的次数是 10次，那么 a2在 a1之后的概率是 10/100，这一概率对应的熵值是-log2(10/100)=3.321 9 bit，远小于 0阶的熵值-log2(100/10000)=6.643 9 bit。采用 2阶、3阶或更高阶次的自适应算术编码，可以获得更高的压缩率。

2 建模与算法实现

2.1 自适应编码模型

用high_count和low_count表示ai对应的子区间上下界，用scale表示已读入符号总数。读入符号ai时，scale加1，与该符号对应的子区间的上界及后面子区间的上下界值都加1。high和low表示编码输出数值range的上下界，其初始值分别为0xffff和0，则可以通过公式(2)确定range的范围。在编码过程中，用二进制表示的range的数值范围越来越小，当high与low的最高位相同时，则把最高位二进制作为码流输出，且使high与low左移一位，high末位补 1，low末位补 0。当 high与 low十分接近没有相同最高位时，就产生下溢，这时需要扩大range使后面的编码继续进行，记录下溢位数，并在下次编码时作为码流输出，用于解码时保持一致。图2显示了自适应编码的基本过程。

2.2 多阶上下文模型

符号在某符号序列后出现的概率往往高于其在整个信息中的概率，这是多阶自适应算术编码能显著提高压缩效果的关键。在1阶上下文模型中，使用数组来统计符号出现的次数是可行的，但对于2阶、3阶或更高阶的上下文，数组大小将按指数级增长（256n+1），采用树结构[4]存储出现过的上下文可以解决存储空间问题。因此，多阶上下文模型是一个包含多个链表节点的树形结构，如果根的层次为0，那么树的层次对应了模型的阶，父节点对应低阶上下文，子节点对应高阶上下文，各层链表节点构成了该层符号表，链表节点中指向父节点和子节点的指针构成了符号序列的上下文关系，形成上下文树。树中只有出现过的上下文才拥有已分配的节点，没有出现过的上下文不占用内存空间。在每个上下文表中，也无需保存所有 256个字符的计数，只有在该上下文后面出现过的字符才拥有计数值。由此，可以最大限度地减少空间消耗。

对于一个未知的上下文，需要用到一个特殊的记号——转义码，用来告知解码器下一个上下文在此之前从未出现过，需要使用低阶的上下文进行解码。比如在3阶上下文模型中，刚刚编码过 a1a2a3，现在要编码a4，而在a1a2a3后面从来没有出现过a4，这时需要输出转义码，并进入2阶上下文表查找a4在a2a3后面出现在次数，如果找到则用2阶中的概率为a4编码，否则输出转义码进入1阶上下文表查找，如仍未找到，则输出转义码进入最低的0阶上下文表，如果a4从未出现过，则转到一个特殊的转义表，表内包含0～255所有符号，每个符号的计数都为1，并且永远不会被更新，任何在高阶上下文中没有出现的符号都可以退到这里按照1/256的概率进行编码，随后将a4加入到各阶符号表中。符号流“a1a2a3a4…ai…”的上下文环境处理过程如图 3所示，其中节点是简化了的链表节点，实线箭头表示指向高一阶上下文的指针（叶子节点指针为空），形成上下文表，虚线箭头表示指向低一阶上下文的指针（根节点除外）。

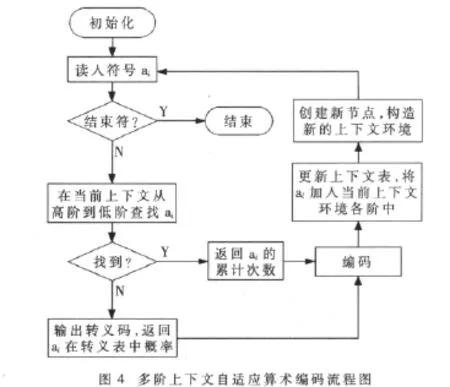
多阶上下文模型在初始化时，需要创建转义表及初始上下文表，上下文表中各阶链表节点中设置符号表、符号计数器、符号表大小计数器以及上下文指针。读入符号后，在当前上下文表中从高阶到低阶查找符号表，找到后输出其在符号表的累计次数，进而计算其概率区间，否则进入转义表，输出固定的概率值1/256，然后进入编码器编码，编码完成后，更新上下文表，将符号加入到当前上下文各阶节点的符号表中，并更新符号计数器。多阶上下文自适应算术编码流程如图4所示。

3 性能测试与比较

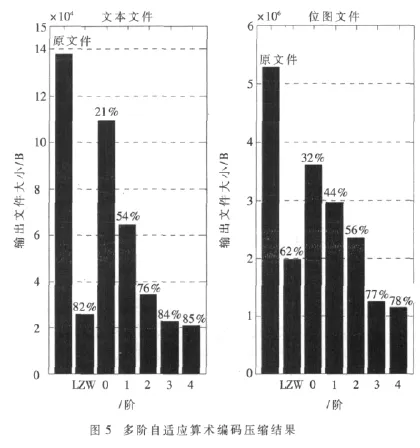
压缩率是反应压缩效果的重要指标，其计算式为：（1-输出文件大小/输入文件大小）×100%，其值越大，压缩效果越好。为测试程序性能，选取了不同大小和不同类型的文件进行压缩，试验结果如图5所示，其中文本文件是大小为137 979 B的历史文献节选，位图文件是分辨率为1 680×1 050、大小为 5 292 054 B的电脑桌面文件。从结果中可以看出，多阶自适应算术编码能达到很好的压缩效果，压缩率随着阶次的升高而提高，但提高幅度逐渐降低，3阶和4阶就能达到比较显著的压缩效果。与参考文献[5]中改进的LZW算法比较发现，0～2阶的压缩效果要差于LZW，但从3阶开始，压缩效果就要优于LZW。

考虑到多阶自适应算术编码的特征，其对上下文相关性强的文件压缩可以达到更高的压缩率。为此，选取了一个内容相关性强的文本文件和一个背景变化不太大的位图文件，如表3和表4所示显示了多阶自适应算术编码与LZW以及WinRAR的比较结果。可看出，多阶自适应算术编码对上下文相关性强的文件压缩效果从2阶开始就优于LZW，而3、4阶就能较明显的好于WinRAR。

表5记录了多阶自适应算术编码和LZW算法对上述4个文件压缩所需要的时间，从表中可以看出，低阶编码消耗的时间最多，3阶、4阶左右消耗的时间最少，再高阶次消耗的时间反而上升。 另外，对于一般性文件，LZW消耗的时间明显少于本文多阶算法，但是对于上下文相关性强的文件，本文多阶算法可以明显少于LZW。

表3 压缩比较(原文件：110 522 B)

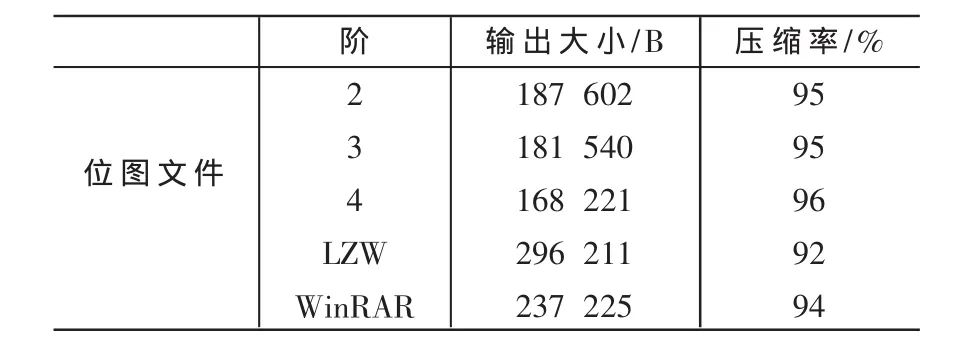
表4 压缩比较(原文件：3 932 214 B)

表5 多阶自适应算术编码与LZW算法时间消耗比较（单位：s）

从以上性能测试与比较中可以得出，本文研究的多阶自适应算术编码在3阶、4阶时可以获得满意的压缩率，而且消耗的时间最少，在整体上压缩效果最佳。

[1]陈玮，杨名利.基于 FPGA的 JPEG2000自适应算术编码器设计[J].计算机技术与发展，2006，16(10)：211-213.

[2]DAMIAN K，MAREK D.Improved context-adaptive arithmetic coding in H.264/avc[C].Glasgow：EUSIPCO，2009：2216-2220.

[3]杨文涛，刘卫忠，郑立新.多阶上下文自适应二进制算术编码实现[J].华中科技大学学报(自然科学版)，2007，35(3)：42-45.

[4]谢林，虞露，仇佩亮.基于上下文的自适应二进制算术编码研究[J].浙江大学学报(工学版)，2005，39(6)：910-914.

[5]张凤林，刘思峰.LZW*：一个改进的LZW数据压缩算法[J].小型微型计算机系统，2006，27(10)：1897-1899.