基于PCA和PNN的发动机故障诊断研究
李凤春
山东理工职业学院电气工程系 山东 272105
0 前言
概率神经网络(Probabilistic Neural Network,PNN)是在径向基函数(RBF)神经网络的基础上发展而来的一种前馈型神经网络,最早是由D.F.Specht博士在1989年提出。其实质是基于贝叶斯最小风险准则的一种并行算法,特别适合于模式识别及分类。PNN结构简单,训练简洁,当获得足够多且足够代表性的样本后可直接使用,无需训练过程,在一般的模式识别问题中都能取得比较理想的效果。
但PNN在训练样本数量较大冗余度较高的情况下,分类效果往往不理想。主成分分析(Principal Component Analysis,PCA)是一种重要的多元统计分析方法,它将显示变量作一定的线性转化产生数量较少的隐式变量,降低原始数据空间的维数,再从新的隐式变量中提取主要变化信息及特征,这样既保留了原有数据信息的特征,又消除变量间的关联、简化分析复杂度,从新的数据空间中提取符合相应的主元数,同时也消除了部分的系统噪声干扰。目前PCA被广泛用于神经网络,主要用来降低神经网络输入向量的维数,进而提高神经网络的模式识别效率。为此,本文提出了一种基于PCA和PNN的故障诊断方法,克服了训练样本数据冗余度比较大的缺点,并以某汽车发动机的故障诊断为例验证了所提算法的有效性。
1 主成分分析法
主成分分析法(PCA)通常又称为Hotelling变换或者K-L变换,它是研究如何将多指标问题转化为较少综合指标的一种重要方法,是一种基于目标统计特性的最佳正交变换,这是因为它具有很多重要的优良性质,如变换后产生的新的分量正交或者不相关,以部分新的分量表示原矢量时均方误差最小,变换矢量更趋确定、能量更趋集中等,这使它在特征选取、数据压缩等方面都有着极其重要的应用。
设x=(x1,x2,⋅⋅⋅,xn)T为n维随机矢量,则PCA的具体计算步骤如下:
(1)将原始观察数据组成样本矩阵X,每一列为一个观察样本x,每一行代表一维数据。
(2)计算每一维的均值,即计算样本矩阵X每一行的均值,并对矩阵中的每个样本x做如下处理:
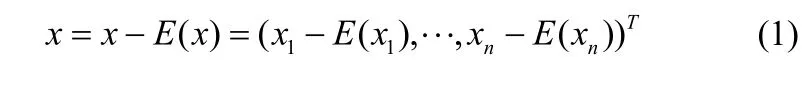
这样做的目的是简化利用新生成的分量估计原始目标特征时估计式的形式。
(3)计算样本的协方差矩阵:

(4)计算协方差矩阵Cn的特征值λi及相应特征向量,其中i=1,2,…,n。
(5)将特征值按由大到小顺序排列,并按照下式计算前m个主元的累积贡献率:
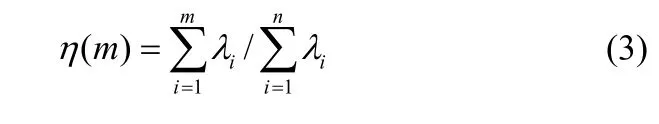
(6)取前m个较大特征值对应的特征向量构成的变化矩阵'T:

(7)通过Y=(T')TX计算前m个主成分,达到降低维数的目的。
若用压缩后的数据Y估计原始数据,即数据恢复,可以按照以下步骤进行处理:
(1)估计原始数据矩阵:
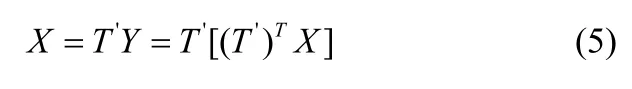
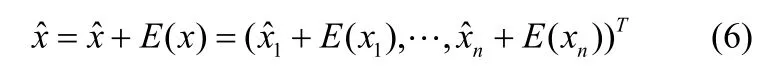
(2)对估计矩阵X每一维分别进行加均值处理:由于变换矩阵'T仅由协方差矩阵的部分特征向量构成,因此,恢复数据不可能完全与原始数据相同,差异程度由所选的m个主元的累积贡献率衡量。
2 基于PCA和PNN的汽车发动机故障诊断研究
2.1 发动机模型描述
发动机是最常用的动力设备之一,在国民经济和日常生活中起着举足轻重的作用,广泛应用于各个行业,已成为某些行业中不可或缺的关键设备。它具有零部件多且相互关联、运动复杂、工作环境恶劣等特点,因而发生故障的可能性也比较大,而且发生故障后,将会影响机械系统的正常运转,直接或者间接地造成巨大的经济损失。发动机在运行过程中,最常见的故障一般分为两类,一类是油路故障;另一类是气路故障。这两类故障的检测与诊断一直是研究的热点。
本文以某汽车发动机的故障诊断为研究实例。在发动机运行过程中,选取AI、MA、DI、MD、TR和PR共计6个变量作为特征参数。其中,AI为最大加速度指标,MA为平均加速度指标,DI为最大减速度指标。
在进行故障诊断时,首先根据PCA对所提取的特征参数进行降维处理,然后利用 PNN进行诊断,诊断模型如图 1所示。
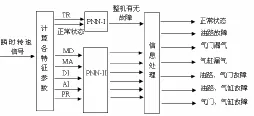
图1 基于PNN的发动机诊断模型
2.2 仿真研究
由图2可见,我们设计了两个PNN进行故障诊断。PNN-I的输入层有两个节点,对应TR和正常状态;样本模式层有两个节点,分别对应正常和故障两种模式;输出层有两个节点,分别对应正常和故障两种状态。
PNN-II的输入层有5个节点,分别对应5个特征参数为AI、MA、DI、MD、PR;模式层有十个节点,对应每个节点的正常和故障中的10组模式;输出层有4个节点,分别对应油路故障、气门漏气、汽缸漏气和正常4种状态。所谓信息处理就是通过输出的4种状态综合判定实际输出究竟是单故障还是复合故障。
选用发动机中的1号汽缸进行分析。经过分析,该汽缸一共出现了3种故障,分别为油量少、气门漏气和汽缸漏气,再加上正常状态,可以认为一共有4种故障模式。利用二进制数格式描述这4种故障模式,如表1所示。这4种故障模式通过现场试验和对历史资料的收集分析,可以得到4组故障样本数据,如表2所示。
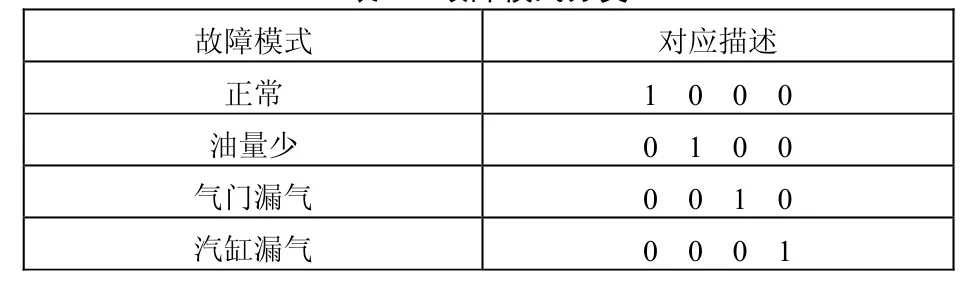
表1 故障模式分类
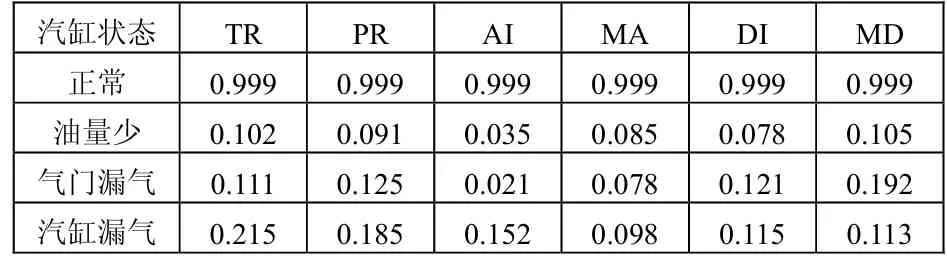
表2 故障样本数据
由于这些数据之间相差都不大,因此,不需要再进行归一化处理。将表2所得的故障样本数据用PCA方法进行分析处理,得到降维后的数据,如表3所示。

表3 降维后的故障样本数据
利用这些降维后的故障信息作为网络的训练样本,从而创建一个概率神经网络用于故障诊断。PNN的创建方法和RBF网络的创建方法非常相似,代码为:
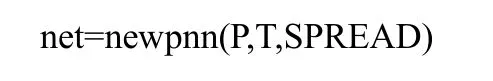
其中,P和T分别为输入向量和目标向量,SPREAD为径向基函数的分布密度,默认为 0.1。为了更好地分析SPREAD对网络性能的影响,这里将SPREAD设置为5个值,分别为0.1、0.2、0.3、0.4和0.5。
函数 newpnn已经创建了一个准确的概率神经网络,可以利用该网络进行故障诊断和分析了。
首先,检验网络对训练数据的分类:
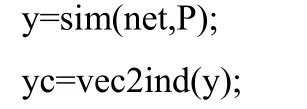
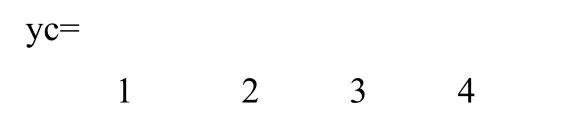
不同的 SPREAD值对应的概率神经网络的输出结果都是一样的,即:由此可见,网络成功地将故障模式分为了4类。为了进一步检验网络的分类效果,接下来给出了一组测试样本数据,如表4所示。这组数据都来源于真实的故障信息,因此可以有效地检验网络的分类性能。
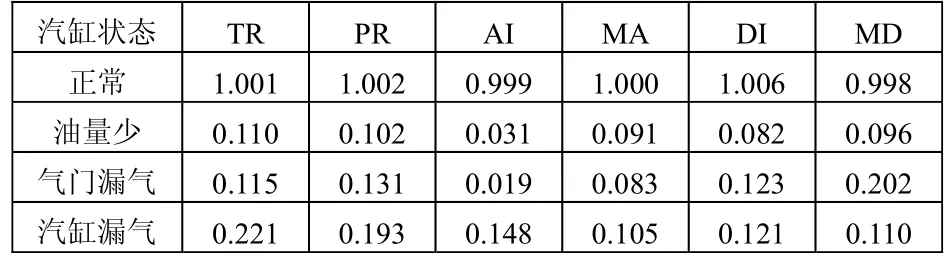
表4 测试样本数据
同样的,根据PCA方法对表4所得的测试样本数据进行分析处理,并得到降维后的数据,如表5所示。

表5 降维后的测试样本数据
利用表5降维后中测试样本对概率神经网络进行测试,代码为:
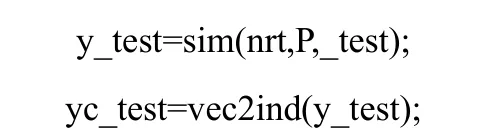
输出结果为:
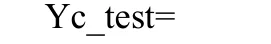
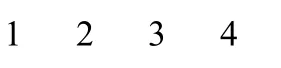
由此可见,网络的分类是正确的。也就是说,概率神经网络成功地诊断出了这4种故障。
3 结语
本文提出了一种基于PCA和PNN的汽车发动机的故障检测与诊断算法。仿真研究结果表明,与传统的PNN相比,该方法在降低数据维数的同时保证了很高的识别正确率,进一步说明了PCA很好地保留了原始特征信息。在保证较高的分类识别率的前提下,简化了识别算法、提高了识别算法的推广能力和运算速度,这对于分类识别系统尤其是实时分类识别系统具有重要意义。
[1] Specht D F.Probabilistic neural network [J].Neural Network.1990.
[2] 李冬辉,刘浩.基于概率神经网络的故障诊断方法及应用[J].系统工程与电子技术.2004.
[3] 常羽彤,张鹏.基于 PNN 的飞机发动机故障诊断研究[J].微计算机信息.2007.
[4] 邢杰,萧德云.基于 PCA 的概率神经网络结构优化[J].清华大学学报(自然科学版).2008.
[5] 李军梅,胡以华,陶小红.基于主成分分析与 BP神经网络的识别方法研究[J].红外与激光工程.2005.
[6] 杨荣英,苗张木.BP神经网络主成分分析法在交通需求预测中的应用[J].武汉理工大学学报.2002.
[7] 黄孝彬,刘吉臻,牛玉广.主元分析方法在火电厂锅炉过程检测中的应用[J].动力工程.2004.
[8] 孙文爽,陈兰祥.多元统计分析[M].北京:高等教育出版社.1994.

