流线化生产中加工时间与瓶颈的关系分析

潘春荣

(①广东工业大学机电工程学院，广东广州510006;②汕头大学、汕头轻工装备研究院，广东汕头515063)

流线化生产是指工件从前一站加工结束立即传送到下一站加工，直到末站完成成品的加工，中间没有缓冲。这种生产方式是现代生产管理的标志。流线化生产具有固定的加工顺序和加工站，当生产线的某个加工站的生产作业结束，而下一站的生产作业还在继续时，上一站的工件无法传递到下一站进行加工的状态称为卡住;当生产线的某个加工站的生产作业已完成，而上一站的生产作业还正在进行时，即无法得到上一站的工件来加工而处于等待的状态称为挨饿。发生卡住和挨饿的现象是由于站与站的加工时间的差异性造成的。为了避免这种现象的发生，可采用平衡理论来保持生产过程作业时间的一致性。

虽然站间的缓冲区可以减缓加工站间的卡住与挨饿现象，但缓冲的发生必然增加在制品数量和生产车间的空间，增加企业成本。虽然平衡理论［1，2］能够改善挨饿和卡住的现象，但由于加工时间的波动性容易造成站与站的加工时间的差异性，进一步影响加工站的卡住或挨饿。因此避免加工站的挨饿和卡住，特别是瓶颈站的挨饿和卡住，对于提高流线化生产的生产率具有重要意义。

1 加工时间对瓶颈站的影响分析

由约束理论［3］可知，生产率是由瓶颈站的加工时间决定的。因此，提高瓶颈站的利用率是提高系统生产率的关键。虽然提高非瓶颈站的利用率对提高生产率及在制品的水平并不起决定性的作用，但非瓶颈站的加工时间调度不合理也容易造成瓶颈站的挨饿和卡住，从而影响到系统的生产率。在生产过程中，有些关键设备的加工站，由于企业的资金或技术的原因，往往成为生产瓶颈，难以消除。所以如何合理地调度非瓶颈的加工时间，充分发挥瓶颈站的作用是企业提高生产管理水平的重要措施。

为了方便阐述，采用下列符号:

i:加工工件的序号，i=1，2，…N

Tin:第n站加工第i工件的加工时间，1≤n，i≤N

p:设为瓶颈站，1≤p≤N，加工时间:Tp＞ Tq，p≠q，q＜N

1.1 瓶颈站的挨饿

瓶颈站的挨饿是由瓶颈站之前的加工站造成的。当瓶颈站(第p站)加工第i工件时，其前一站(第p-1站)加工第(i+1)工件，而前第二站(第p-2站)加工第(i+2)工件，前第三站(第p-3站)加工第(i+3)工件，以此类推，第一站加工第(i+x-1)工件。对于瓶颈发生饥饿的如下情形:

(1)当瓶颈站的前一加工站的加工时间大于瓶颈站的加工时间时，即，也就是瓶颈站等待其前一站的工件加工结束时，造成第(p-1)站变为瓶颈站，而原瓶颈站(第p站)变为非瓶颈站而出现瓶颈漂移，使原瓶颈站(第p站)挨饿。

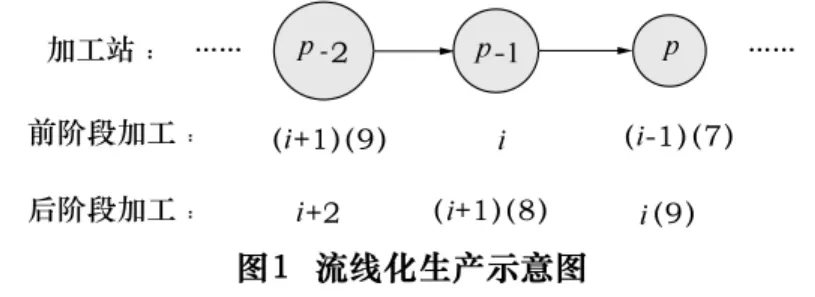
(2)在瓶颈站之前一站的加工时间小于瓶颈站的加工时间，并不意味着不会发生饥饿［4］。事实上，瓶颈站是否发生饥饿与瓶颈站之前的所有站存在一定的关系。如图1所示，虽然第(p-1)站的加工时间小于第p站(图中前括号内的参数表示工件号，后括号内的参数表示加工时间)，由于前阶段的第p-2站的工件(i+1)的加工时间较长，使得第p-1站的工件i的加工结束时，出现第p-1站等待工件i+1的现象，造成工件i+1的延迟加工，最终出现瓶颈站(第p站)的挨饿。由于，但是，。以此类推，若工件(i+1)在瓶颈站之前的第p-1站、第p-2站、…、第x-h站(1≤h≤x-1)加工时间为式(1)

第i工件、第i-1工件、…、第i-h工件(1＜h＜x-1)在瓶颈站的加工时间为式(2)

为了避免瓶颈站的挨饿，必须满足式(3)

通过式(3)能够判断各加工站的加工时间是否造成瓶颈站的挨饿，从而判断是否影响系统的生产率。

1.2 瓶颈站的卡住

瓶颈站的卡住是由瓶颈站后面的加工站造成的。当瓶颈站(第p站)加工工件i时，第(p+1)站加工第(i-1)个工件，第m站加工第(i+p-m)工件时，由于瓶颈站后面的任一站(设为f站)的卡住必然造成卡住站前一站(第f-1站)的卡住，从而引起连锁效应，即造成第(f-2)站、第(f-3)站、……、瓶颈站(p站)的卡住。为了避免瓶颈站的卡住必须使瓶颈站的加工时间大于其后各站的加工时间，即

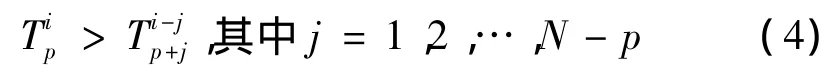
从上述分析可知，为了避免瓶颈站的挨饿或卡住以获得瓶颈站的最大利用率，关键是合理地调度非瓶颈站的加工时间。

2 建模

虽然改变加工工艺可以改善流线化生产，但是，通过现场实验评估每个方案的可行性是不实际的。所以仿真验证提供了一个可行的方法，特别是对于实时动态的作业时间的波动。

eM-Plant是一个面向对象的图形化的建模和仿真平台。它采用进程交互(即事件调度法与活动扫描法的结合)进行仿真，由仿真时钟推进，将满足条件的事件从将来事件列表(FEL:future events list)移到当前事件列表(CEL:current events list)，然后按活动扫描法对CEL中的每个记录进行扫描。当条件为真时，执行相应的活动，修改系统的状态并确定下一事件。当CEL中所有记录处理完成后，结束对CEL的扫描，推进仿真时钟，再将FEL的最早发生事件移到CEL中，直至仿真结束。本文利用eM-Plant建立生产线仿真模型，分析非瓶颈、瓶颈站的生产时间和利用率，验证瓶颈站出现卡住和挨饿现象。

eM-Plant将制造系统中的基本对象和辅助对象划分为4类:物流对象、移动对象、信息流对象和服务类对象［5］。制造系统是一种典型的离散系统，受随机因素影响较大，离散系统仿真算法较多，其中面向进程的进程交互法更符合生产线的实际情况，而eMPlant采用的就是进程交互法［6］，这有助于加工时间随机波动的仿真。

(1)采用物流对象EventController来模拟一个时钟、SingProc来模拟加工站、entity来模拟加工工件及flowcontrol实现加工工件流量的控制。对于加工时间长的加工工艺，可以采用并行加工站的方式来降低改工序的作业时间以满足流线化生产的生产节拍。例如singleproc1和singleproc2的加工时间为16个时间单位，但该工序的生产节拍为8个时间单位。从singleproc出来的工件采用flowcontrol的百分数的出口控制方式实现加工和控制的要求。

(2)采用信息流对象的method实现各种控制策略包括产生加工时间的随机数。

(3)采用服务类对象Chart将仿真系统的运行数据形象地反映给用户，实现用户与仿真模型之间的交互界面。

3 实例

以汕头某公司生产减速器的厂家为例，减速器的箱体生产时间为60 min，蜗盖的生产时间为60 min，蜗轮的生产时间为20 min及蜗杆生产时间为120 min。

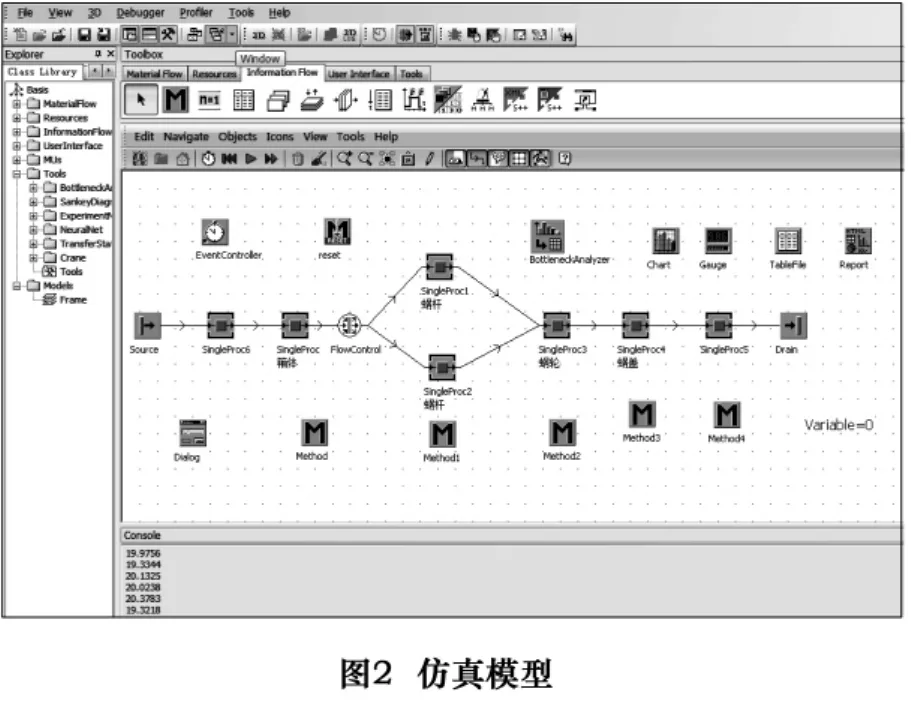
利用上述式(4)可知，上述蜗杆的加工是瓶颈工序，容易造成卡住。为了实现流线化生产，可以采用一定的加工工艺减少瓶颈工序的加工时间，如采用并行加工站及改变装夹具从而降低瓶颈站的加工时间。对于生产线的流线化生产能够从理论上进行计算，但实际的生产中不能避免各加工过程的波动性。利用上述方法建立仿真模型，如图2。通过仿真分析非瓶颈站的时间波动对瓶颈站的卡住和饥饿的影响。

表1 加工时间的随机数

针对上述作业时间的波动对生产线的影响进行分析。由正态分布曲线可知，当标准正态分布区间(-1.96，1.96)或正态分布区间(μ -1.96σ，μ +1.96σ)的概率为95%，意味着考虑加工时间的两倍标准差的时间波动的概率为95%，这对于生产线的管理决策而言具有重要的意义［7］。利用这个原理，在仿真模型中非瓶颈站(设为蜗轮站)的加工时间波动选用正态分布函数(当函数的均值为20，标准差为2)，其它非瓶颈站仍处于加工时间稳态值20个时间单位。通过控制程序 singleproc3.proctime:=z_normal(1，20，2)控制，并在method中采用print语句及eM-Plant的主控制窗口显示出正态分布函数所生成的随机加工时间，如表1。

通过上述模型的仿真，非瓶颈站蜗轮加工站的时间波动对瓶颈加工站蜗杆站的卡住和饥饿的统计如图3所示。当蜗轮加工站发生上述随机时间波动时，对瓶颈站造成4.06%的卡住及0.21%的饥饿。从上述的数据可知，该蜗轮站的加工时间波动更容易造成瓶颈站的卡住。所以，为了避免时间波动对瓶颈的影响，可以在瓶颈站之前一站增加少量的缓冲，使得瓶颈站卡住时，可以把工件放入缓冲。增加少量的缓冲有利于系统提高生产率，最终系统获得近优或最优。

4 结语

通过分析非瓶颈站与瓶颈站之间的加工时间的关系，可避免瓶颈站的挨饿和卡住现象，为调整系统的加工工艺提供了依据。通过eM-Plant的仿真模型的仿真，实现在时间波动的条件下知晓加工站之间的卡住和饥饿情形，为提高瓶颈的利用率、生产率及实现流线化生产提供了参考。对于目前产品寿命越来越短、多批次和少批量来说，加工站的时间波动越来越大，在波动中保证瓶颈站的最大产出率，对于生产管理水平的提高具有重要的理论和现实的意义。

1 POWELL.S.G.Buffer Allocation in Unbalanced Three-station Serial Lines［J］.International Journal of Production Research，1994，32(9)

2 POWELL.S.G.，D.F.PYKE.Buffering Unbalanced Assembly Systems［J］.IIE Transactions，1998(30)

3 GOLDRATT EM，Theory of constraints.1990，New York:North Press.

4 WU H-H，YANW-F.a Design Model for the Protective Capacity of Serial Production Lines［J］.Journal of the Chinese Institute of Industrial Engineers，2004，21(2)

5 贾晨辉，张浩，陆剑峰.离散制造系统规划与仿真建模研究［J］.计算机工程与应用，2007，43(3)

6 彭旺明，张晓川.Em-plan t在生产线作业仿真中的应用研究［J］.武汉理工大学学报(交通科学与工程版)，2004，28(4)

7 K.K，SURY R J.a Study ofWork-time Distributions on Unpaced tasks［J］.IIE Transactions，1987(7)