基于 ANSYS的钢筋混凝土浅梁单调加载变形的数值模拟

李文华 赵彦革 张 吉 潘 宁 杜文博 方 伟

(1.山东莱钢建设有限公司,青岛 266071;2.中国建筑科学研究院,北京 100013)

1 引言

1967年,Scordelis等人[1]首次将有限元法引入钢筋混凝土梁构件的分析。通过数值模拟(或叫做仿真分析)的方法对结构和构件的力学性能进行分析研究,与传统的试验分析方法相比,在资源的耗费等方面,都具有明显的优势。国内外的学者在混凝土梁的有限元分析方面做了大量的工作,初期的研究者有不少通过自编的程序和算法[2],采用较多的简化后(比如采用平面单元等),对梁进行分析并取得了一些初步成果。近些年,随着大型通用有限元软件 ANSYS等的发展,由于单元、材料、加载方式都是开放的,能采用三维的实体单元建模,研究者们无需繁琐的编程,完全可以使用该软件量身制作分析问题的模型,所以在建筑结构、构件的数值模拟中应用越来越广泛,也发表了大量的研究文献[4]～[6]。但文献中通常只是针对某个试验结果,采用单一的有限元模型进行分析,对多模型计算对比及影响参数进行详细对比研究的尚不多。研究方法大多基于试验取得的数据,反复调整有限元模型输入参数进行试算,最终使得有限元分析数值结果与试验结果接近,此时得出的参数值很难具有普适性。而数值模拟研究工作最终所需要达到的目标,是得出一套比较标准化的参数设置方法去指导数值分析,通过数值分析或者辅以少量的类似于材料强度的标定试验工作后,就能对结构或构件的性能进行预估,并且估计值的可靠度是可接受的。本文在借鉴这些文献中的做法后,对钢筋混凝土浅梁的加载变形过程数值模拟方法做了进一步的研究,对影响计算的主要影响因素做了较全面的对比分析。建筑结构中浅梁的破坏形式有多种,如斜拉破坏、剪压破坏、弯曲破坏等,当梁的破坏机理存在不同时,能不能采用相同的参数设置对其进行分析,也是本文探索的问题。

2 分析模型

2.1 有限元模型及单元选择

分析选用的单元与所选有限元模型紧密相关,以往文献中的有限元模型以分离式和整体式为主。ANSYS公司在最新版本(12.0版本)中推出了组合单元,基于该单元可使用组合式模型对结构和构件进行分析。

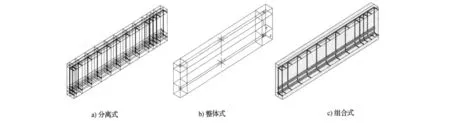
图1 钢筋混凝土梁的有限元模型

2.1.1 分离式模型

钢筋与混凝土采用不同单元分别建模(如图1a))。该模型的优点是可以准确的考虑钢筋的位置,在精细的有限元分析中该优点则更为突出,比如需考虑钢筋与混凝土之间的相对滑移影响时,可通过在钢筋与混凝土单元之间植入连接单元实现;缺点是建模工作量大,且计算较耗时。

模型中不论受拉纵筋、受压筋还是箍筋,均可按一维构件建模。通常情况下,由于其截面比较小,可不考虑其抗弯性能[2],所以分析时较多的选用 PIPE或 LINK系列单元(杆单元)。混凝土基本上都选择 ANSYS软件内置的 SOLID65单元建模,因为该单元除了具备一般实体单元 SOLID45的特性之外,还具有开裂、压碎功能,是单元库中最适合于做混凝土结构非线性分析的单元。

2.1.2 整体式模型

通过对单元刚度矩阵的处理,将钢筋和混凝土揉合在一起,类似于将钢筋弥散在混凝土材料中,形成一种新的复合材料。由于不需建出每根钢筋的位置,建模比较容易,并且节点自由度较少,所以分析速度一般比较高。该模型的缺点是钢筋的位置无法准确指定,钢筋的多少通过配筋率指定,因此钢筋作用的考虑是比较粗略的;钢筋与混凝土之间的滑移也不能考虑(如图1b))。

2.1.3 组合式模型

该模型基于新开发的 REINF264单元,REINF264单元是通过在现有实体基单元的基础上,植入杆单元或梁单元形成(如图1c)),同一个基单元中可以指定多根同向或不同向的钢筋杆单元,当基单元使用高次单元时,以较少的单元数就能获得较高的分析精度,用于在整体结构分析时,将能明显提高分析效率。组合式模型具有能准确的考虑钢筋的位置优点,但是钢筋与混凝土之间还只能是完全变形协调,目前的实体基单元还不包括 solid65单元,也就是说,软件暂时无法自动考虑开裂与压碎。

在本文中,考虑到组合式模型还不完善,尚需自定义材料,所以对比分析时只针对前两种有限元分析模型,使两者在单元网格尺寸等条件相同的情况下,以试验记录数据为对比对象,通过对比分析研究两者用于加载变形过程模拟的有限元模型的可靠性与效率。

2.2 材料模型

2.2.1 钢筋

加载变形过程模拟分析时应当考虑钢筋的塑性性能,常用的钢筋非线性模型有理想弹塑性和双线性强化弹塑性模型。理想弹塑性模型计算结果偏保守,本文是将计算结果与试验结果对比,故结合原试验情况,箍筋与受压筋采用双线性随动强化模型,梁底纵筋采用多段线性随动强化模型,采用随动强化模型的原因是该强化模型可以反映“包辛格效应”,与钢筋材料性能一致。

2.2.2 混凝土

(1)本构关系

ANSYS软件中常用的内置本构模型有 4种,即线弹性、多段线性等向强化(MISO)、多段线性随动强化(MKIN或 KINH)与 D-P模型,4种模型对应不同的屈服准则。所有屈服准则都可以结合内置的Willam-Warnke破坏准则一起使用。多段线性等向强化与随动强化模型的屈服面均基于 Mises准则,在主应力空间中,屈服面为一圆柱面(轴线为等倾轴),即屈服面与静水压力无关;D-P模型屈服准则为两参数的屈服准则,是修正的 M-C准则,该准则的屈服面在偏平面上为圆形,且外接于 M-C准则[13]的不等边多边形,拉压子午线均为直线,随着静水压力的增加,屈服面逐渐增大,具体形状通过内聚力与内摩擦角两个参数来控制;从两个准则的屈服面形状来看,基于 D-P准则的屈服面更接近于三轴试验的结果,且可以通过设置内摩擦角与膨胀角的关系采用相关或非相关流动法则;但是混凝土材料的内粘聚力与内摩擦角方面的试验资料比较少,缺乏可供借鉴的经验,目前数值模拟中仍以使用 Mises准则居多。

多段线性等向强化与随动强化本构模型都要求输入混凝土材料的单轴应力 -应变关系,美国混凝土结构设计规范 ACI318-05中没有明确给出混凝土结构或构件分析用的混凝土受压应力 -应变关系[10],本文采用了文献[12]中由美国学者 Hongnestad建议的曲线。不论是等向强化还是随动强化模型,材料的单轴应力 -应变曲线输入时,均需输入全应力与全应变,第一应力 -应变点计算出的斜率等于指定的初始弹性模量,指定的最后应力 -应变点后未输完的部分按软件默认置为水平直线,但随动强化模型则可输入下降段。

(2)开裂

有限元分析中的裂缝模型,主要有离散式、弥散式与内嵌式三种。离散式裂缝模型中,裂缝为开裂部位单元的边,随着裂缝的开展,需重新划分单元网格,计算处理复杂。内嵌式裂缝通过改造单元形函数实现,计算处理也比较复杂。目前较多采用弥散裂缝模型,ANSYS提供的裂缝模型是固定弥散式裂缝模型,且假定在垂直裂缝方向单元不能承受拉力,但可以承受压力;裂缝面的剪力传递系数分张开与闭合两种状态讨论,分析经验表明钢筋混凝土梁有限元分析时,张开裂缝剪力传递系数可取 0.3～0.5,裂缝闭合时可取0.95～1.00。

本文将混凝土的弥散式裂缝模型与上述四种混凝土本构模型结合,采用分离式与整体式有限元模型分别计算,所有分析模型见表1。

表1 分析模型汇总表

3 对比分析过程介绍

3.1 原试验概况与对比结果

本文采用文献[7]中的试验梁作为分析对象。该文献试验数据记录详细,已有较多的国内外学者[8-9]成功采用其试验数据检验了他们的有限元模型。该文共做了 4组共 12个简支梁试件,变化的参数有剪跨比,配筋率等。本文选用了其中 C组的两个梁试件,因为该组梁试件的截面及配筋与工程中的情况较接近,并且一个试件(A-1)按剪压形式破坏,另一个试件(A-3)按弯曲破坏形式,能够代表结构破坏时梁的两种主要破坏模式。梁截面尺寸及试验的加载条件如下图所示,两构件的截面尺寸相同,宽 305mm(12in),高 552.45mm(21.75in);其中A-1构件净跨 3.658m(12ft),A-3构件净跨 6.401m(21ft);底部纵向为 9号钢筋,初始弹性模量为 2.05×105MPa,屈服强度 552MPa;顶部受压钢筋为 4号钢筋,初始弹性模量为 2.0×105MPa,屈服强度为345MPa;箍筋为 2号钢筋,初始弹性模量为 1.9×105MPa,屈服强度为 325.5MPa。

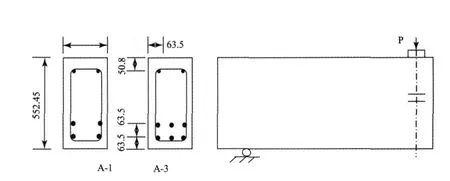
图2 试件截面尺寸与加载方式示意图

试件与荷载都具有对称性,为了提高分析与计算效率,取 1/4梁进行内力分析;所有的分析模型都采用 SOLID 65单元模拟混凝土,分离式模型中的钢筋采用 LINK8单元模拟,整体式中钢筋通过 SOLID65单元的实常数输入。文献[7]中已说明,为了避免粘结及锚固破坏,纵向钢筋端部采用了特制锚具以保证锚固效果,所以模型中未考虑混凝土与钢筋之间的滑移。原文未明确给出混凝土初始弹性模量,本文根据文献[10]中公式即按Ec=4739′(MPa)计算,其中 fc′为混凝土的受压强度。A-1与 A-3试件的混凝土抗压强度分别为 24.1MPa(3500psi)与 34.48MPa(5000psi),故对应的初始弹性模量分别为 2.32×104MPa与 2.8×104MPa;抗拉强度分别为 3.86MPa(559psi)与4.34MPa(629psi)。

为了与实际情况相符合,加载前先施加重力,以模拟加载前重力形成的效应对计算结果的影响;分析时通过两个荷载步来实现,第二步加载时软件可自动在重力荷载形成的位移场等基础上进行分析。计算时使用以往研究人员在分析中常用的参数设置,网格尺寸取为 75mm,使用力加载模式,力收敛准则(收敛容差为 3%,选 L2泛数);不考虑混凝土的压碎,但考虑混凝土的开裂;破坏准则定义用的 8个参数中只输入单元抗压与抗拉强度,其它参数按默认计算。在 D-P模型中,混凝土材料的内聚力与内摩擦角的值按文献[11]中提出的公式计算,其它未特殊说明的参数按默认值设置。分别按表1中的模型进行分析,各种模型计算的梁中点的挠度与荷载关系曲线与文献[7]中试验结果对比如图3和图4所示。

从图3和图4中可以看出,整体式模型与分离式模型计算结果大体相同,当荷载加到 17kN左右,此时结构刚度都有一个突降,这是由于混凝土开裂造成的(从通用后处理模块中调入该加载时刻的开裂图进行判断),因此该荷载值可以作为梁构件的开裂荷载,该现象与文献[6]中得出结论相同;开裂后的一段加载范围内,分析与试验记录的荷载 -挠度曲线出现了偏差,分析值比试验值小,但两者形状基本一致,出现偏差的可能原因有下两个方面:其一,Willam-Warnke破坏准则中的约定,该准则约定只要某一点的三个主应力中有一个为拉应力,则应力组合值达到破坏曲面时,单元以开裂形式破坏,导致开裂过早;其二,开裂以后不考虑混凝土软化段的承载能力也使得分析值比试验值小。

当加载到接近极限荷载时,按 D-P模型、线弹性模型、MISO模型计算极限荷载(不收敛时上一子步所施加的荷载)却均大于试验的极限荷载或与之接近。对于以剪压形式破坏的 A-1试件,计算极限荷载比试验值大得较多;而弯曲破坏形式破坏的 A-3试件,破坏主要是由于钢筋屈服导致,极限荷载计算值受是否考虑混凝土软化与压碎的影响较小些。依据以上现象可初步推测是建模时没有考虑混凝土的受压软化与压碎所致。

从图3和图4中结果可看出,关闭混凝土压碎功能,虽能计算获得较完整的荷载位移曲线,但通常会导致极限荷载的计算值偏高,尤其在使用线弹性与 D-P模型对剪压破坏形式的梁进行分析时。因此在确定构件的极限荷载时,不应简单以计算收不收敛为依据。较为合理的做法是:结合梁的破坏形式与钢筋和混凝土中的应力、应变情况后再做出判断。通过后处理模块调出各加载子步跨中底部纵筋的应力以及顶部混凝土的总应变(弹性应变 +塑性应变),以确定计算不收敛时的荷载是否为真实的极限荷载。当计算不收敛时混凝土的总应变过大时,应当以混凝土极限应变对应的加载值为最终极限荷载;当计算不收敛时而混凝土总应变过小或钢筋尚未屈服时,应调整计算模型及参数,得到合理的极限荷载。比如本文两试件按分离式线弹性模型与 D-P模型计算时,混凝土极限应变均偏大(达 0.005以上),得出的计算极限荷载将是偏大的;此时,若以混凝土总应变均在 0.003位置(对应A-1构件的跨中挠度为 0.017m,A-1构件的跨中挠度为 0.038m)的荷载作为极限荷载,比计算不收敛时极限荷载要准确得多;四模型中以 MISO模型计算值与试验值最接近。而整体式模型,虽有相同的加载位移曲线,但是其钢筋应力不能准确确定。所以下面的分析只针对分离式式模型并采用 MISO本构模型情形。

图6显示了 MISO模型计算出的破坏荷载时的裂缝分布与试验结果对比,ANSYS中计算的破坏时的单元开裂情形与试验值是一致的,剪压破坏的 A-1构件,破坏时跨中部位裂缝开展不深,且靠近支座位置裂缝往加载梁顶延伸,发展成为主要的裂缝;而以弯曲破坏的 A-3构件,接近支座部位裂缝都开展不深,而跨中位置,由于底部纵筋屈服,产生较大开裂变形,加载到极限荷载时裂缝已开展至梁顶。

从图6结果可知,通过数值模拟得出的破坏形态是准确的。

另外,通过后处理模块可以查看所有单元中静水压力值的大小,从计算结果看来,两梁构件绝大部分区域的静水压力值都没有超过fc′,所以混凝土材料的破坏准则定义时,可只输入单轴状态下的抗压与抗拉强度,其它参数均可按软件的默认值设定。

3.2 影响参数的灵敏性分析

3.2.1 网格尺寸的影响

采用有限元求解力学问题,通常情况下,单元越小,数值解与理论解越接近。但对于混凝土结构,因其具有开裂特性,如果单元过小,在较小荷载作用下,就有可能因为个别单元破坏而导致整体刚度矩阵的秩有所减少,导致计算精度下降,也有可能导致计算不收敛,因此有必要对网格尺寸对加载变形曲线的影响进行研究。一般情况下通过加密网格的做法对模型试算,前后几次计算结果变化在限定的小值之内时,即可认为网格密度已经足够。本文以 0.1m、0.09m、0.08m、0.075m、0.07m、0.06m、0.05m网格大小对梁进行计算,各种网格尺寸计算加载与位移曲线与试验对比结果见图7。从图7中可以看到,随着网格细化,A-1试件的刚度稍有下降,并且计算极限荷载降低;A-3构件刚度基本没有受到影响,而计算极限荷载也有降低。

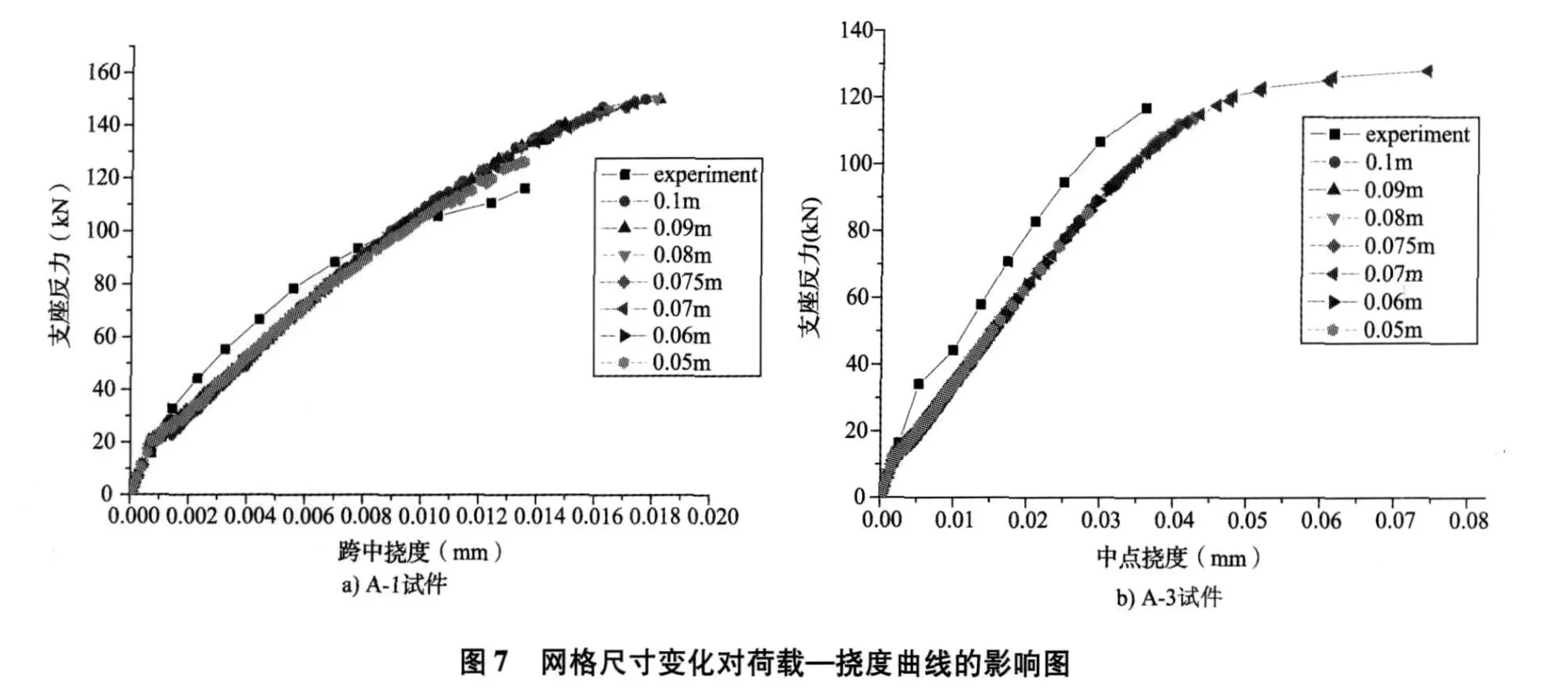
3.2.2 开裂面剪力传递系数的影响

本文将剪力传递系数取为 0.2、0.3、0.4、0.5、0.6五种情形对两个试件进行计算。各种开裂面剪力传递系数计算加载与位移曲线与试验对比结果见图8,从对比结果可看出,随着剪力传递系数的降低,构件的刚度与极限荷载均有下降,A-1构件下降比 A-3明显,但是下降幅度都不大。

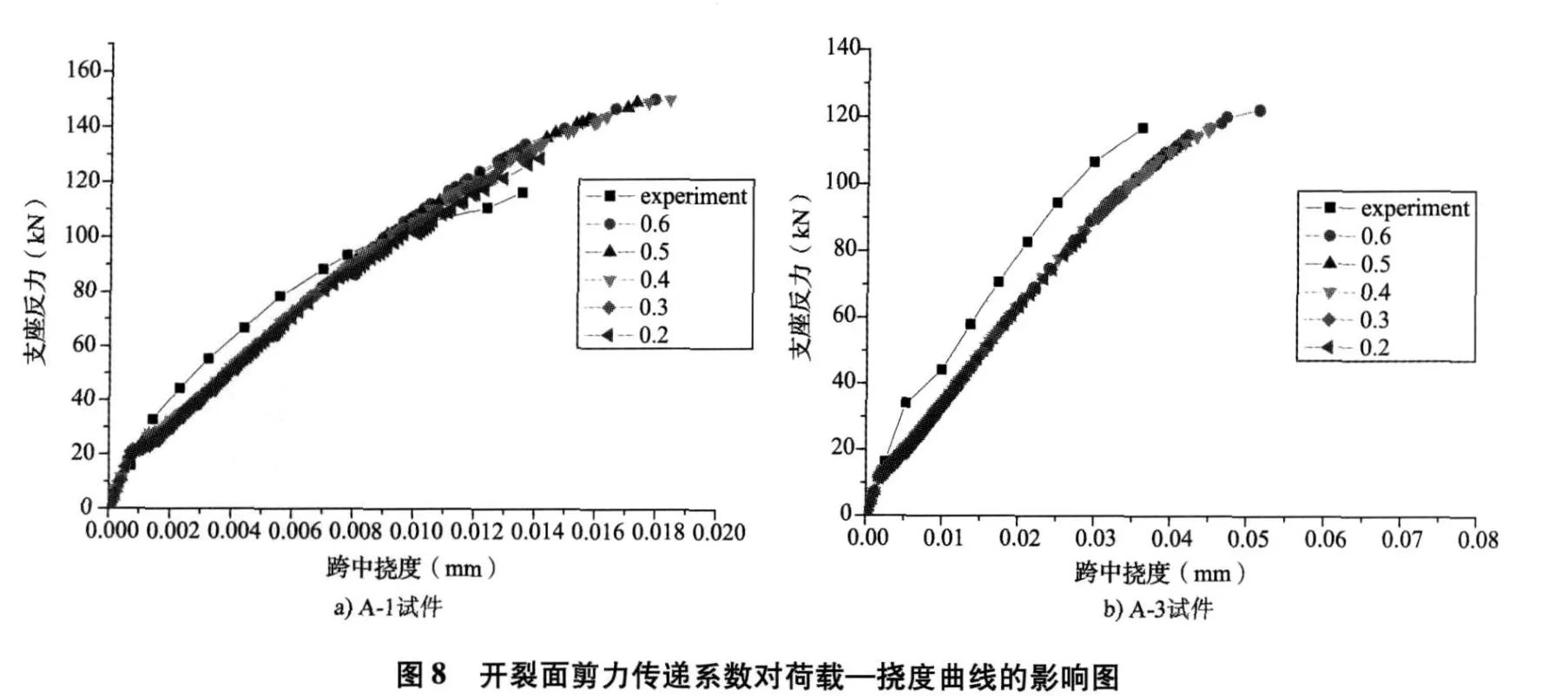
图9 力收敛准则变化对荷载—挠度曲线的影响图

3.2.3 加载方式与收敛容差的影响

加载方式分位移加载与力加载两种,两种加载方式每荷载步内的收敛准则均可以选用位移收敛准则、力收敛准则或位移与力双控的收敛准则(软件的默认值)。本次分析的两个梁试件,本构关系为线弹性与 D-P理想弹塑性时,使用任意的收敛准则,都能得到合理的极限承载力值。而多段线性等向强化、随动强化,当使用位移收敛准则时,在很小的荷载下就产生了计算不收敛,所以计算时均选用力收敛准则。

本文将收敛容差取为 5%、4%、3%、2%、1%五种情形对两个试件进行计算,打开自动时间走步控制选项(以便软件自动根据上一荷载子步的迭代次数来优化本荷载步内荷载子步的大小)。各种收敛容差下计算的加载与位移曲线与试验对比结果见图9,从图9中结果看出,收敛容差的变化对两个试件的计算荷载变形曲线的影响都非常小。

4 结论

混凝土梁的荷载位移过程的数值模拟影响因素众多,如有限元模型、混凝土的本构模型、网格密度、开裂面剪力传递系数与收敛容差等。本文采用分离式与整体式有限元模型,以单因素的方式,对主要影响因素进行对比分析,得出了以下一些结论:

1)对剪压与弯曲破坏的梁模拟时,分离式与整体式有限元模型计算的加载变形曲线大致相同;与试验值相比,使用线弹性与D-P模型计算的加载变形曲线极限荷载偏高,而 KINH模型的计算值偏小,MISO模型计算值最为接近。梁构件的极限荷载,不能简单取定为求解不收敛时的施加荷载,尚应结合压区混凝土的压应变与受拉纵筋的拉应力后确定。

2)从对比结果看来,网格大小从 0.1m降到0.05m,对加载变形曲线影响不大,因此可认对于本文中尺寸大小的梁构件分析时,采用 0.1m网格计算,结果即已收敛。但从前后几次计算结果相差不大判断是否收敛还是太具主观性,要量化离散误差还有待于能给出类似于弹性问题中的百分比能量误差的程序的出现。

3)位移收敛容差设成 1%～5%、开裂面剪力传力系数由 0.6降到 0.2,对剪压形式破坏的 A-1构件计算结果的影响较大些,对弯曲破坏的 A-3构件影响非常小;从数值看,对两构件计算结果影响都不大。

目前分析模型中没有考虑混凝土的软化阶段承载力对构件性能的影响;混凝土的裂缝模型为固定弥散裂缝模型(更准确的方式应当是旋转裂缝模型);没有考虑箍筋约束对混凝土的影响,考虑约束作用后,混凝土延性性能等都会有变化。这些问题都将影响数值模拟的适用性,还需要进一步探索。

[1]Ngo D..Scordelis A C.Finite element analysis of reinforced concrete beam[J].ACI,1967,64(3):152-163.

[2]周氐,等译.钢筋混凝土有限元分析——技术现状报告[M].南京:河海大学出版社,1988.

[3]朱伯龙,董振祥.钢筋混凝土非线性分析[M].上海:同济大学出版社,1985.

[4]罗如登.Ansys中砼单元 Solid65的裂缝间剪力传递系数取值[J].江苏大学学报,2008,(3):169-172.

[5]梅毕祥,许明,贾益纲等.基于 ANSYS的混凝土极限荷载影响因素分析[J].南昌工程学院学报,2009,(2):35-40.

[6]Antonio F.Barbosa,GabrielO.Ribeiro.Analysis of Reinforced Concrete Structures Using ANSYS Non linear Concrete Model[J].Computational Mechanics New Trends and Applications,Barcelona,Spain,1998.

[7]Bresler B,Scordelis A.C..Shear strength of Reinforced Concrete Beams[J].ACI,1963,60(1):51-74.

[8]Cedolin L.,Nlison A..A Convergence Study of Iterative Methods Applied to Finite Element Analysis of Reinforced Concrete[J].International Journal for Numerical Methods,1978,Vol.12.

[9]姜峰,徐勇,王朝波.基于网格自适应的钢筋混凝土随机有限元分析[J].建筑科学与工程学报,2007,(3):69-73.

[10]贡金鑫,魏巍巍,胡家顺.中美欧混凝土结构设计[M].北京:中国建筑工业出版社,2007.

[11]李云安,葛修润等.岩 -土 -混凝土破坏准则及其强度参数估算[J].岩石力学与工程学报,2004,(3):770-776.

[12]江见鲸,陆新征,叶列平.混凝土结构有限元分析[M].北京:清华大学出版社,2005.

[13]ANSYS,Inc.Theory reference for ANSYS and ANSYS Workbench 12.0.1,2009

[14]K.J.Willam and E.D.Warnke.Constitutive Model for the Triaxial Behavior of Concrete[J].Int.Assoc.Bridge Struct.Engng.Proc.,1975,Vol.19,p.174.