风荷载作用下建筑结构表面的压力分布研究

周建芬,王玉强

(浙江水利水电专科学校,浙江 杭州 310018)

浙江省沿海地区遭受超强台风损失较严重,次数较多,个别地区遭受台风损失较为典型,特别是温州、台州、丽水等几个地方.研究建筑结构在风场作用下的压力分布对结构的优化设计具有指导作用.台风的中心气压低、风力强、降雨强度大、防御难.数值模拟高强度风场对结构的作用还有很大的难度,目前针对一般强度风场对建筑结构作用的研究开展的较多.利用数值风洞技术模拟建筑表面的风压,避免了风洞试验费用高,周期长等不足之处.数值风洞在增加费用的情况下,可以根据研究的需要改变流场和结构的相关参数,对研究对象进行多方面的分析研究.

1 数值风洞技术

数值风洞方法与直接的风洞实验相比较,具有模拟真实风环境的能力,可以构造与建筑物实际尺寸相当的计算模型,可以按实际的风环境进行仿真和模拟,避免了风洞试验只能进行缩尺试验的不足.

我国规范上采用体型系数表示建筑面上的平均风压系数,表达式如下：

式中：μsi—面上第i测点的风压系数;

Ai— 第i测点的面积;

A—面积之和.

本研究的建筑结构为钝体形状,建筑物在地表边界层内的流场中存在,钝体周围的流场由撞击、分离、再附、环绕和漩涡等确定.

计算不可压缩流体湍流运动时将湍流看作平均运动和脉动运动两部分,将湍流运动的任何参变量都分解为时间平均值和脉动值,即

p′—脉动压力.

数值模拟绕钝体速度和压力场的分布时采用改进的k-ε模型,即MMK模型,该模型方程如下[1]

式中：Pk—某点的压强;

vk—涡团粘度;

S—平均切变率张量;

k—湍流动能;

Cu—待定常数;

ε—耗散率.

1.1 顺风向情况下柔性结构静动力风荷载和位移方程

由风速实录可知,顺风向除了平均风速还包括脉动风速分量.当结构物刚性很强时,脉动风引起结构物风振惯性力不明显,可略去,当结构物较柔时,除静力风荷载外,还应该考虑风振惯性力,即风振动力荷载,则总风荷载表达式为

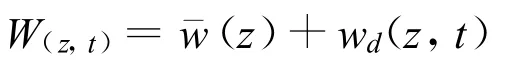
式中：W(z,t)—具有某一保证率的总风荷载;(z)—z高度处的平均风荷载;wd(z,t)—具有某一保证率的风振动力风荷载.

受风敏感的柔性结构属竖向一维悬臂结构,该结构沿竖向的质量和刚度分布不均匀,现将其抽象为一维悬臂的无限自由度体系.其运动方程可表示为

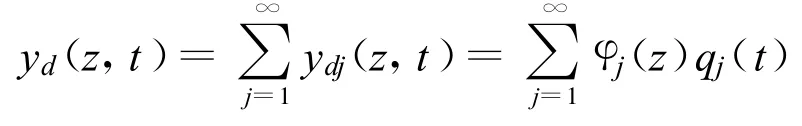
式中：yd(z,t)—第j振型的动位移;

φj(z)—第j振型z高度处的坐标;

qj(t)—第j振型的广义坐标.

则结构z高度处最大峰值位移可表示为

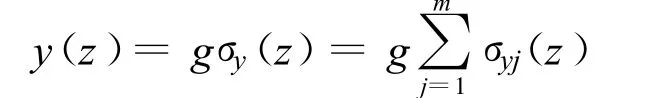
g—峰因子,其表达式为[2]

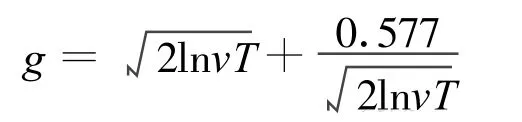
g的常用范围为3.0-4.0.

1.2 横风向情况下结构风振方程

当风作用在结构物上时,就会在该结构物两侧背后产生交替的漩涡,且将由一侧向另一侧交替脱落,形成卡门涡列.卡门涡列使建筑物表面的压力呈周期性变化,且作用方向与风向垂直.该作用引起结构发生与风向垂直的涡激振动.该振动是伴随着漩涡的出现而产生的强迫振动,当振动增强后,又会有由振动控制的涡流发生,表现出自激振动的特性.当风速在某一特定风速范围内,该振动才变得较为显著.

对于竖向悬臂结构,在横风向涡激动力荷载作用下,其运动方程为

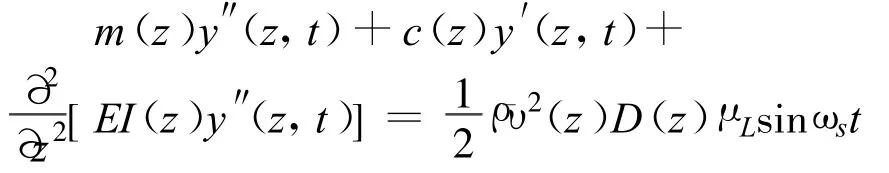
式中：y″(z,t)—不同质点处的水平加速度;

y′(z,t)—不同质点处的水平的速度;

ρ—空气的质量密度;

¯υ—来流的平均速度;

D(z)—物体在垂直于平均流速的平面上投影特征尺寸;

μL—升力系数.

2 边界条件

本文应用Fluent软件的用户自定义函数(UDF)功能实现与试验风特性一致的平均风速与湍流特性等规律.

(1)平均风剖面

对C类地貌,平均风速按指数形式表示.为对于数值风洞,k-ε模型计算的是湍动能k和湍耗散率ε的输运方程.

(2)湍流特性

风洞试验常给出湍流强度与湍流积分尺度,本文采用日本建议的Ⅲ类地貌湍流强度公式拟合,因此需要将上述湍流强度及积分尺度进行一定的转化.

实践结果表明,由于上述关系基于湍流各向同性假设,将使建筑迎风面的湍动能及风压系数等偏大.

3 计算结果与分析

将风洞试验测得的风压与改进的k-ε模型计算的结果进行比较可以看出改进的k-ε模型对风压力计算给出了较好的结果[3],见图1、图2.

图1 风洞试验

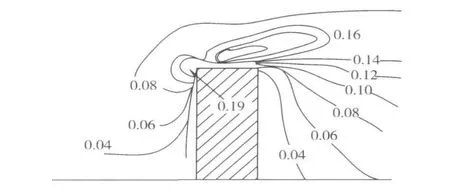
图2 改进的模型

柱体建筑物正面受到风压作用,为正值,而背面、侧面和顶面则受到吸力,为负值.数值分析结果如图4,从图中可以看出,对钝体建筑物,正面中间偏上处正压力最大,在两边及靠近下部处压力则较小,气流对该面有向下流动的趋势,而且绕两侧和顶面流动,大约在建筑物2/3高度处,气流有一正面停滞点,气流从该停滞点向外辐射扩散.在该点以上,流动上升越过建筑物顶面,在该点以下,气流向下并流向地面,在这一区域,其动能比同一水平高度的来流大,因此它可以呈现反风向流动,能量逐步损失直至在地面分离点处于静止,在气流向下滚动时,在建筑物迎风面紧靠地面形成了水平滚动,成为驻涡区.

建筑物侧面的压力分布规律为气流在侧面的角线处分离,在离顶部1/3高度范围内分流稳定,而下部的风速明显比同一高度来流风速大,由漩涡引起的竖向掺混使侧面的流动沿高度方向趋于均匀.

顶面的压力来源于正面1/3以上气流,这部分气流流向顶面,顶面上部的风有较低的分离流线,导致了较早的再附着.

4 不同的结构体形在气流场中的荷载分布规律

经过数值模拟计算分析,对于不同倾斜的屋面,平均风流线分布,见图3.

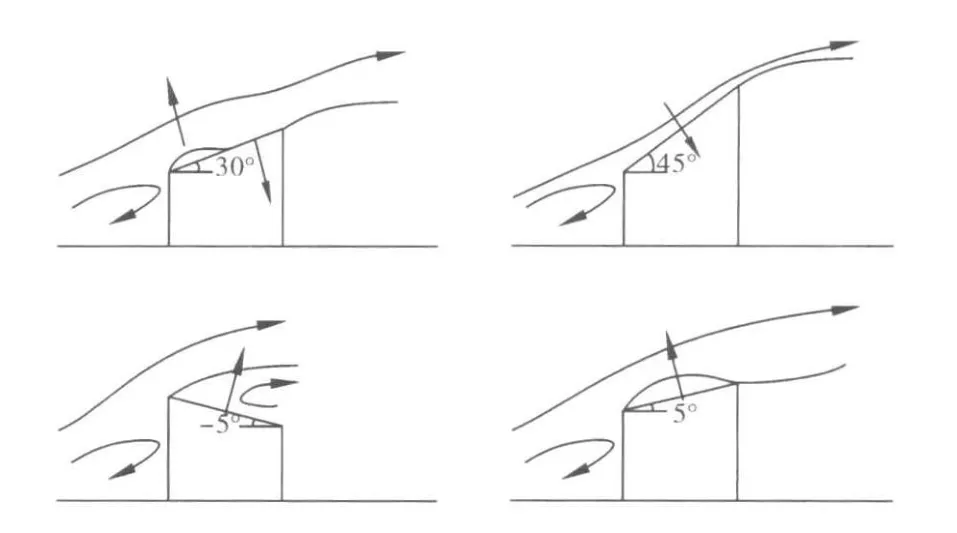
图3 屋面倾角对风流线分布的影响

屋面风压力有再附着现象,当屋面倾角为30°左右时,屋面部分受到向上升力部分受到向下压力.当屋面倾角大于45°时,屋面气流在附着现象不再出现,屋面受到压力作用.其它倾角的屋面存在再附着现象,屋面受到上升力作用.

[1] S.MURAKANI,A.MOCHIDA,K.K,et al.These Proceedings[M].Landon：J.Wind Eng.Ind.Aerodyn Press,1997.

[2] 埃米尔◦希缪,罗伯特◦H◦斯坎伦.风对结构的作用——风工程导论[M].刘尚培,项海帆,译.上海：同济大学出版社,1992.

[3] 张相庭.结构风工程：理论规范实践[M].北京：中国建筑工业出版社,2006.