义乌降水气候分析中的面雨量计算及其应用比较

王忠红,赵贤产,余 菲

(1.义乌市水文站,浙江 义乌 322000;2.义乌市气象局,浙江 义乌 322000)

0 引 言

在某地降水量的气候变化分析中,或气象部门发布降水量趋势预报时,一般都使用气象站的单站降水量统计值.显然,单站降水量是不能完全代表该区域某时期的降水量,而应用面雨量的统计值进行分析,才能代表该区域某时期的降水量;同样,流域的流量、江河的抗洪能力以及水库的蓄洪规模都与流域的平均降雨量(即面雨量)密切相关.因此,客观地、简便地计算面雨量具有重要的意义.方慈安等[1]研究了几种流域面雨量计算方法并进行了比较;毕宝贵等[2]研究了面雨量计算方法并进行海河流域的应用;徐晶等[3]对流域面雨量估算技术进行了综述,但新技术探测资料如雷达、卫星云图等资料的连续积累时间均不长,在气候变化研究时有一定不足;董官臣等研究了面雨量的预报问题[4],但用面雨量资料作降水气候分析较少见.本文试图通过用多站点算术平均法和泰森多边形法获得的义乌面雨量,与单站降水量进行气候变化分析的比较,来说明义乌区域面雨量简捷的计算方法和面雨量应用的意义.

1 面雨量的定义

面雨量系指单位面积上的降雨量即某一特定区域或流域的平均降雨状况.面平均雨量P可表示为：

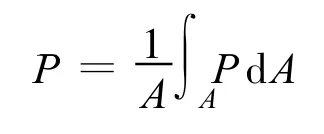
式中A为特定区域面积,P为有限元dA上雨量.

2 面雨量计算方法

面雨量的计算方法很多,主要有泰森多边形法、逐步订正格点法、三角形法、算术平均法、格点法、等雨量线法等.据有关文献资料介绍,算术平均法简便易行,但只适用于流域面积小、地形起伏不大,且测站多而分布又较为均匀的流域;格点法能较好地反映降水的连续性;等雨量线法精度高,但较多地依赖于分析技能,而且操作比较复杂,不便于日常业务使用;泰森多边形法或三角形法,考虑了各雨量站的权重,而且当测站固定不变时,各测站的权重也不变,比算术平均法更合理,精度也较高,因此应用较广[5].

3 泰森多边形法的面雨量计算原理

泰森多边形法又叫垂直平分法或加权平均法.该法首先求得各雨量站的面积权重系数,然后用各站点雨量与该站所占面积权重相乘后累加即得.

设每个雨量站都以其所在的多边形为控制面积ΔA,ΔA与全流域的面积A之比为即为该雨量站的权重数.

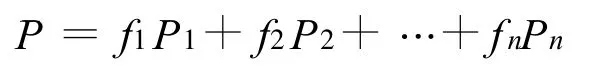
式中f1,f2,…,fn分别为各雨量站用多边形面积计算的权重数;P1,P2,…,Pn,¯P分别为各测站同时期降雨量和流域平均雨量.

此种方法计算面雨量时考虑了测站的权重,精度较高,对测站分布不均匀的流域尤为适合.如实现面雨量计算的业务自动化,在计算机上实现面雨量计算程序自动化,是很有必要的,但其技术难点在于确定环绕每一个站点多边形的唯一性和确定任意多边形的面积上.

4 泰森多边形法的义乌面雨量计算

义乌区域内降水量属气象部门管理的观测站点不多,且时间的连续性记录较差,除义乌市气象局观测站从1959年建站以来均有连续降水记录之外,在2004年以前只有人工观测的气象哨资料,但分布稀少并观测记录有长时间中断情况.2004—2008年陆续建设中尺度自动气象站16个,从研究义乌降水气候变化来说又是不完整的.建国以来属水文部门管理的观测站点数量较多,且长时间连续观测记录完善,为研究义乌区域降水气候变化来说是属最完整的资料.本文采用省级水文部门管理的雨量站观测记录和通用的泰森权重系数来求取面雨量,见表1.其中,选取的11个站点分布见图1,“义乌”为气象观测站,见图1.

表1 各雨量站点权重表

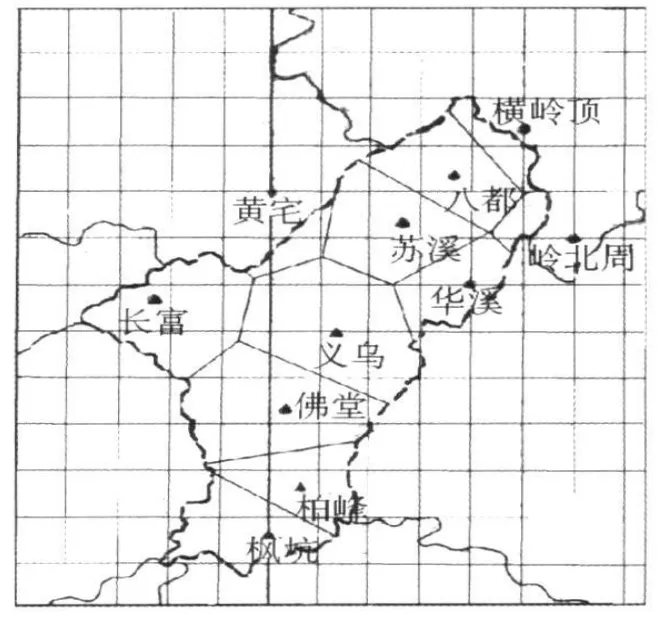
图1 雨量点垂直平分多边形图

其计算公式表述为：

义乌面雨量=横岭顶雨量×4%+石曹头雨量×8.9%+岭北周雨量×1.8%+苏溪雨量×10.1%+华溪雨量×7.4%+黄宅雨量×3.7%+义乌雨量×16.2%+长富雨量×13.3%+义乌佛堂雨量×18.2%+柏峰水库雨量×7.4%+枫坑水库雨量×9.2%

经计算,1982—2008年年度义乌面雨量结果,见表2.同时列入义乌市气象局观测站单站年雨量和义乌境内8站点的多站点算术平均法计算的年面雨量数据,见表2.

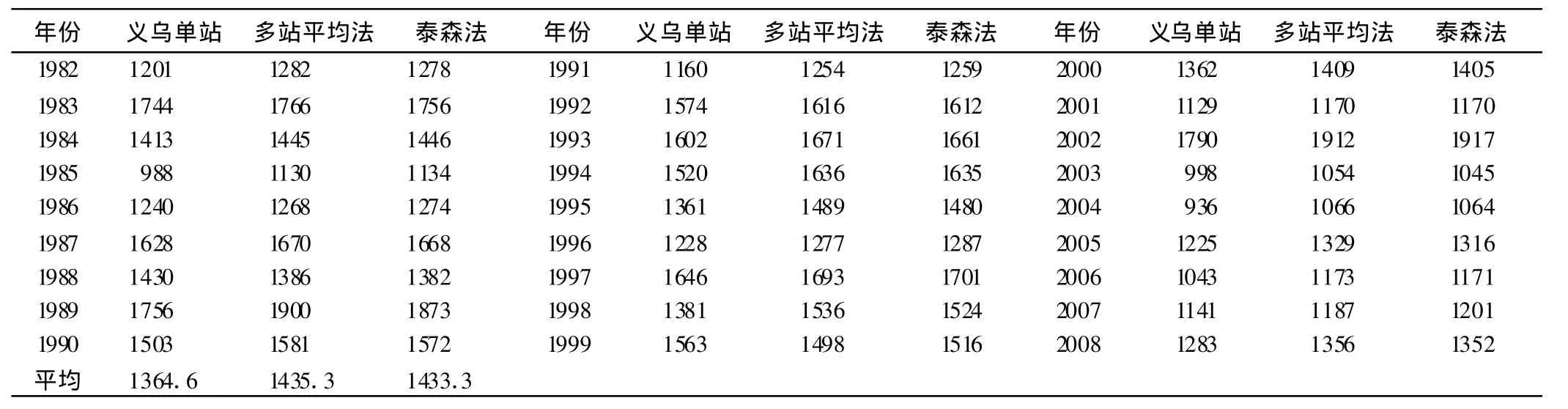
表2 1982—2008年义乌年面雨量mm

5 单点雨量与面雨量的气候分析应用比较

从1982—2008年度降水气候变化迹线来看,义乌市气象局观测站单站雨量随时间变化和义乌境内8站点算术平均法的面雨量或(与)泰森权重计算的数据之间差别较大且明显,其27年的平均结果是：平均法比单站值多70.7 mm、泰森法比单站值多68.7 mm;平均法计算的面雨量与泰森权重计算的数据之间差别相当小,其27年的平均结果是：平均法比泰森法多2 mm,从随时间变化迹线上几乎看不出差别,见图2.

因1959—1981年站点数不一,而用不定站数算术平均法计算的面雨量与单站雨量随时间变化比较,见图3,其差别就更明显,其24年的平均结果是：平均法比单站值多84.8mm(最大年份多202 mm、最小年份少17 mm),其中1959—1962年的3站平均多62.0 mm、1963—1970年的5站平均多 74.5 mm、1971—1979年的6站平均多99.2 mm、1980—1981年的7站平均多111.0 mm.

从义乌市气象局观测站单站雨量和义乌境内3～7站不定站点(1959—1981年)、8站多站点(1982—2008年)的算术平均法计算的面雨量或(与)泰森权重计算的面雨量(1982—2008年)数据等两两之间的相关图也可知它们的差别情况,见图4.从图4中可以看出,平均法与泰森法的面雨量均在相关线上,数据连线和回归线、平滑线基本在同一线上,见图4(a),它们的相关系数为最大,达0.999.其余两两之间的相关性虽然也较好,相关系数达0.954至0.979之间,但实际均有明显差别,见图4(b)、图 4(c)、图 4(d).它们的回归方程有：

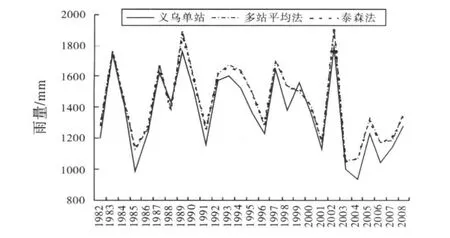
图2 义乌年面雨量数据比较图1

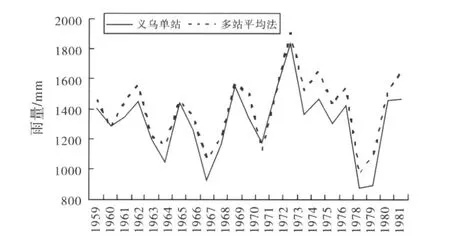
图3 义乌年面雨量数据比较图2

图4 义乌年面雨量数据比较图3

上述式中R泰、R多、R单、R泰不定数分别表示泰森法面雨量数值、多站平均法面雨量数值、义乌单站面雨量数值和不定数站平均法面雨量数值.

从上图和回归方程也可知,面雨量值越小,它们之间的差值越大,而其相关性越差,而雨量值越大,它们之间的差值越小,其相关性越好.究竟原因,主要是降水系统范围大小或降水分布不均而引起：面雨量值越小,说明降水分布不均,系统范围偏小,或仅属局地性降水量大,其它地方降水量偏小;而面雨量值越大,说明强降水的系统范围大,降水分布较均匀,或属全市性大降水日数多.

6 结 语

(1)泰森多边形法与算术平均法计算的面雨量差别较小,而与气象站单站资料比较,其差异均相当明显.

(2)某单站降水资料不能代表该区域降水量,特别是在降水气候分析或某区域降水量趋势预报中,应用区域面雨量值较为科学.

(3)应用面雨量中,用泰森多边形法计算的面雨量比算术平均法更科学、简便、合理.

(4)面雨量值越小,单站法与泰森法的相关性越差;雨量值越大,其相关性越好.

(5)实现面雨量计算的程序自动化和业务化,在实际工作中很有必要和应用价值.

[1] 方慈安,潘志祥,叶成志,等.几种流域面雨量计算方法的比较[J].气象,2003,29(7)：23-26.

[2] 毕宝贵,徐 晶,林 建,等.面雨量计算方法及其在海河流域的应用[J].气象,2003,29(8)：39-42.

[3] 徐 晶,姚学祥.流域面雨量估算技术综述[J].气象,2007,33(7)：15-21.

[4] 董官臣,冶林茂,符长锋,等.面雨量在天气预报中的应用[J].气象,2000,26(1)：9-13.

[5] 蒋金珠,顾鼎仁.工程水文及水利计算[M].北京：中国水利水电出版社,1992：11-12.