基于角速度补偿的捷联天线稳定系统设计
赵 超
(北京华航无线电测量研究所,北京 100013)
0 引言
捷联末制导是各种低成本、小型化制导武器的首选技术方案,它分为全捷联和半捷联两种方式[1]。全捷联方式彻底取消了机械回转机构,体积、成本大幅降低,可靠性提高,但导引头需要较大的瞬时视场。半捷联方式综合了全捷联和传统陀螺稳定平台的优点,保留了机械回转框架,取消了导引头上独立配置的陀螺,利用弹上捷联惯导的姿态信息,实现天线平台的间接稳定。半捷联末制导系统的技术核心是捷联天线稳定算法,它们大都采用以坐标变换为基础的角位置补偿控制方案,通过矢量的惯性指向不变性原理得出理想的伺服系统控制指令[2-3],缺点是技术难度较大,控制精度不高,且用于制导的视线角速度信息提取困难。文献[1,4-5]研究了基于速度补偿的捷联稳定方案,提出采用天线伺服框架角速度和弹体角速度重构天线空间角速度的思想,并设计了匹配滤波器来提高稳定系统对弹体姿态的去耦能力。但是这些研究仅考虑了一维角运动的简单情况,实际上弹体和框架角都是框架三维运动,天线的空间运动关系远比该模型复杂得多。文献[6]考虑了三维运动情况,给出了能够使天线指向惯性空间稳定的伺服系统速度补偿指令。但是没有给出天线稳定控制系统的整体控制结构,没有建立末制导系统跟踪回路和稳定回路的衔接关系,所以只能解决天线的纯稳定问题,而无法处理目标跟踪情况下的天线控制问题。
本文研究了半捷联末制导系统中捷联天线稳定系统设计的问题,提出了一种新的基于角速度补偿的捷联天线稳定控制算法,给出了末制导系统天线稳定平台的完整实现方案,该方案能够解决天线的纯稳定和目标跟踪两种工作模式下的天线控制问题。
1 天线稳定系统工作原理
1.1 陀螺稳定方案
弹载末制导系统的天线稳定系统一般采用两轴回转框架结构,通过直流力矩电机带动天线盘运动以实现俯仰、航向双平面跟踪能力。在导弹飞行过程中,弹体姿态的变化会通过框架摩擦力矩作用在回转框架上,造成天线指向的偏差,因此天线稳定系统还必须能够隔离弹体姿态扰动的影响。在传统的速率陀螺稳定系统中,两个陀螺正交地安装在天线盘背面,可以直接敏感出天线的空间运动角速度,从而实现天线空间指向稳定和对弹体姿态扰动的解耦。天线陀螺稳定系统的原理框图如图1所示,其中:Gs为天线伺服系统传递函数;Gf为速率陀螺传递函数;ε为跟踪回路误差信号;uc为稳定回路指令信号;uf为稳定回路反馈信号;ϑ,λ,θ分别为弹体姿态角、伺服框架角、天线空间指向角,它们之间的关系如图2所示(一维相对运动情况)。

图1 天线陀螺稳定系统原理图Fig.1 Schematic of the gyro stabilization system
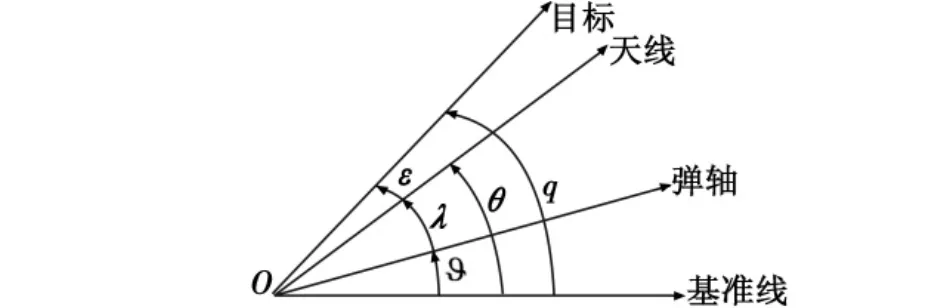
图2 空间角位置关系示意图Fig.2 Schematic of spatial angles
可以看出,天线稳定系统是一个双回路控制系统,外环为跟踪回路,用来检测目标跟踪过程中的角误差,内环为稳定回路,用于控制天线伺服机构电机转速,消除天线指向误差,同时补偿弹体姿态扰动的影响。一般利用速率陀螺输出目标视线角速度信息,采用比例导引方法控制导弹飞向目标。
根据图1,可求出天线稳定回路(虚框中的部分)的传递函数为
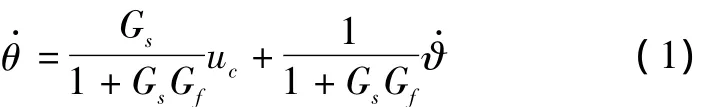
可见,天线运动不仅取决于稳定回路指令信号(与跟踪回路误差有关),还受到弹体姿态运动的影响。理想情况下要求天线指向对弹体姿态解耦,为此控制系统设计中一般希望天线伺服系统前向通道的增益尽可能大,当|Gs|>>1时,稳定系统可实现弹体姿态扰动的去耦。
1.2 捷联稳定方案

图3 稳定回路等效图Fig.3 Equivalent diagram of stabilization loop
在捷联末制导系统中,导引头中取消了陀螺,天线稳定系统中所需的空间绝对角速度信息无法直接测量,此时可以利用弹上捷联惯导给出的弹体姿态运动信息,以及导弹、导引头、天线之间的相对运动关系,使用运动合成方法来重构天线空间运动信息,最终实现天线平台的间接稳定。
需要指出在陀螺稳定方案中,导弹制导所需的目标视线角速度信息可以通过速率陀螺直接提取,而在捷联稳定方案中,惯导陀螺并不跟随视线运动,视线角速度信息只能通过数学方法间接提取。
2 捷联天线稳定系统控制方案
2.1 捷联稳定系统原理与组成
捷联天线稳定系统的原理框图如图4所示,其中测角元件敏感天线框架角运动,捷联惯导敏感弹体姿态运动,这些信息同时送给DSP控制模块,完成天线伺服系统控制量计算,再通过功率放大带动天线伺服机构运动。DSP控制模块是捷联稳定系统的核心,它包括伺服系统校正网络、稳定回路反馈量计算、视线角速度估算3种功能。可见,捷联天线稳定平台本质上是一种数学稳定平台,它依靠数学解算实现天线稳定控制与目标跟踪,同时利用坐标变换关系对目标视线角速度信息进行估算用于比例导引。
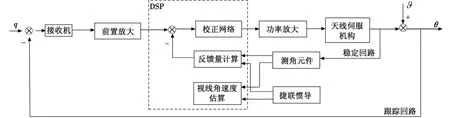
图4 捷联天线稳定系统原理图Fig.4 Schematic of the strap-down stabilization system
根据1.2节中的分析,可以画出捷联天线稳定系统中稳定回路的控制方块图如图5所示。其中:Gs为天线伺服系统;Gcs为与天线同轴的测速元件;Gjl为捷联陀螺;N为测速环节的传感器噪声;uf为稳定回路反馈信号;为目标视线角速度估计输出(用于比例导引);ϑ,λ,θ分别为弹体姿态角、伺服框架角、天线空间指向角。
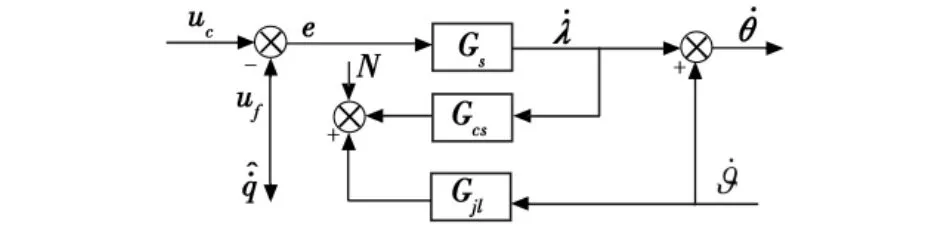
图5 捷联稳定系统原理图Fig.5 Schematic of strap-down stabilization
根据图5可知,在捷联稳定方案中,天线空间角速度为

忽略传感器噪声N的影响,当陀螺通道与测速环节的传递函数完全匹配(即Gcs=Gjl)时,上式简化为
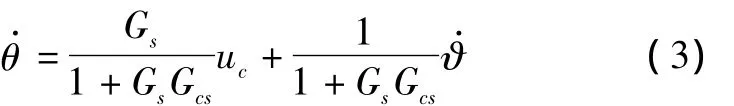
对比式(1)可见,此时捷联方案和陀螺方案的效果完全相同,当|Gs|>>1时,稳定系统可以实现弹体姿态去耦功能。
2.2 角速度补偿信号解算
必须指出:前面的分析仅仅为了说明天线稳定系统的控制原理,其中各种空间角位置的关系(参考图2)只有在一维情况下才是有效的,实际上,因为导弹弹体同时存在俯仰、航向、滚动3个通道姿态运动,导引头天线伺服系统也同时进行俯仰、航向两个通道的运动,这样实际的天线空间运动合成关系就不能按照的简单关系来表示。下面讨论在空间三维运动的情况下,如何确定捷联稳定系统的速度补偿信号uf。
设天线坐标系和弹体坐标系的转换关系如图6所示。

图6 坐标系转换关系Fig.6 Conversion of coordinate system
图中:Oxmymzm为弹体坐标系;Oxayaza为天线坐标系(假定两坐标原点相同);λy,λz为天线平台伺服框架角为框架角速度;ωxm,ωym,ωzm为导弹角速度的弹体坐标系分量。设天线绝对角速度在天线坐标系中的分量为 ωxa,ωya,ωza,显然天线在惯性空间的运动由天线伺服系统的运动和弹体姿态的牵连运动两部分组成,令 ωxas,ωyas,ωzas表示前者引起的天线角速度分量,ωxam,ωyam,ωzam表示后者引起的天线角速度分量。根据坐标变换关系有:
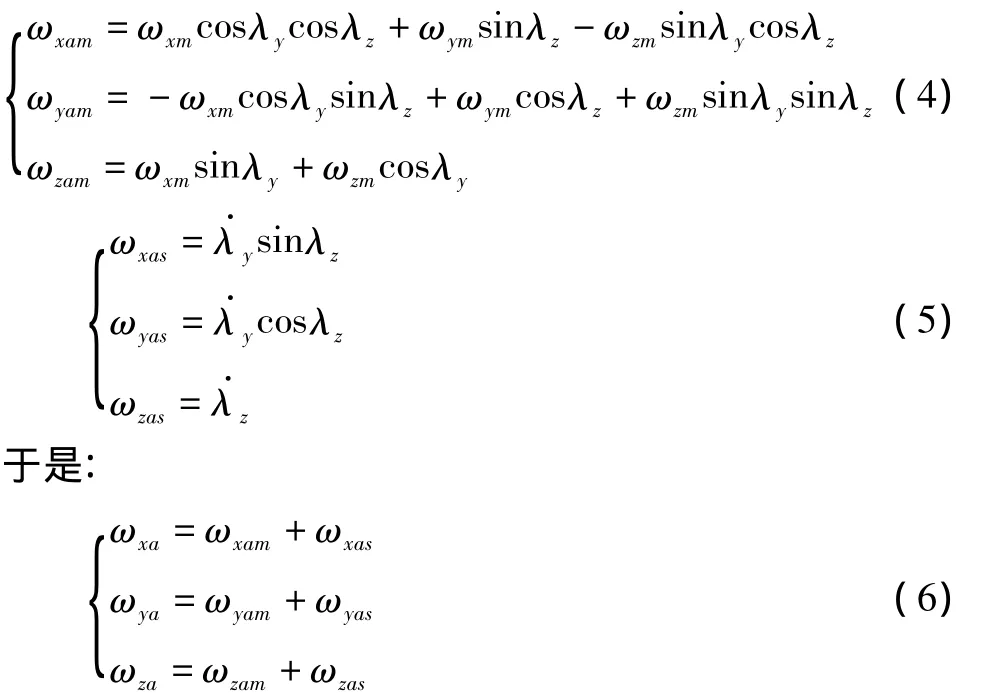
为简化分析,暂时忽略传感器噪声N的影响,并假定图5中两个测速通道的传递函数为匹配环节,即Gcs=Gjl=Gf。
1)天线俯仰通道,取:

将式(8)、式(10)和式(1)对比,可见采用上述速度补偿信号后,捷联稳定方案在最终的控制效果上完全等效于陀螺稳定方案。于是式(4)~式(10)就构成了基于速度补偿的捷联稳定控制算法。
2.3 目标视线角速度估算
在陀螺稳定系统中,速率陀螺所敏感的天线坐标系角速度分量就是目标视线角速度。类似地,在捷联稳定系统中可以按照如下方法得到视线角速度的估计值:
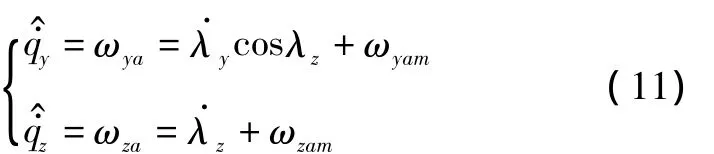
在捷联稳定控制算法中必须注意以下问题:
1)理想的速度补偿效果要求稳定系统的陀螺通道与测速环节的传递函数完全匹配(即Gcs=Gjl),而实际上的测速环节动态特性一般比陀螺要快,要使两者匹配,最实用的方法是设计适当的数字匹配滤波器对测速环节进行处理以提高稳定回路对弹体姿态运动的去耦能力[3-4]。
2)捷联算法中需要对伺服框架角λ进行微分运算,这将会放大传感器的测量噪声,因此天线框架角的测量需要采用高精度低噪声的测角元件(必要时进行滤波处理),或者选用带有角速度输出功能的旋变解调器,如果确需进行微分运算,最好对微分器的输出进行低通滤波后再使用,以免产生过大的控制量超出伺服系统响应范围,最终导致较差的控制效果。
3 仿真结果
对图4所示的捷联天线稳定系统进行数学仿真,有关参数如下:接收机信号处理延迟为0.1 s,前置放大倍数为8,伺服系统电机带载时间常数为0.1 s,校正网络采用PID校正,测角元件的噪声模型取方差为10-6的白噪声,为了克服微分运算对噪声的放大作用,增加一个传递函数为的数字滤波器,同时假设陀螺通道与测速环节的传递特性完全匹配。此外,弹体姿态运动参数取为:ϑx=1·sin2πt,ϑy=1.5 sin10t,ϑz=1.2 sin5t。
捷联天线稳定系统在纯稳定方式下的仿真结果如图7~图8所示。在角速度补偿控制算法的作用下,天线指向表现出较强的弹体姿态解耦能力,其中航向耦合系数约为3.3%,俯仰耦合系数约为4.2%。另假设目标机动为1°的阶跃运动,末制导系统在目标跟踪方式下的仿真结果如图9~图10所示,相应的伺服框架角速度的仿真结果如图11~图12所示。可见,在捷联稳定系统作用下,天线能够较快地跟踪目标角运动,跟踪过程超调量适中、静差不大,能够满足末制导系统的要求。
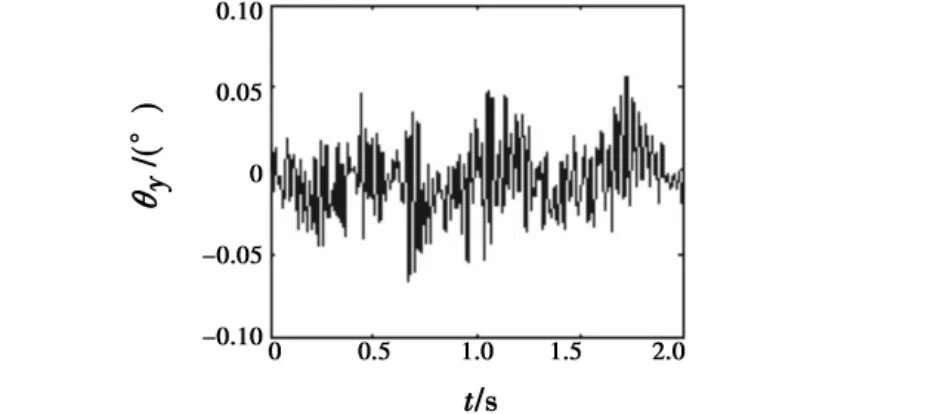
图7 天线指向误差(航向通道)Fig.7 Antenna pointing error(azimuth)

图8 天线指向误差(俯仰通道)Fig.8 Antenna pointing error(elevation)
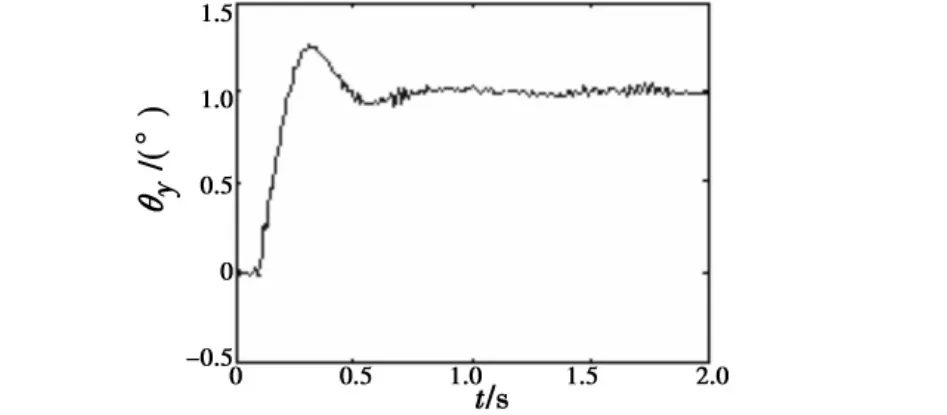
图9 天线空间指向(航向通道)Fig.9 Antenna pointing direction(azimuth)

图10 天线空间指向(俯仰通道)Fig.10 Antenna pointing direction(elevation)

图11 框架角速度(航向通道)Fig.11 Gimbal angular rate(azimuth)
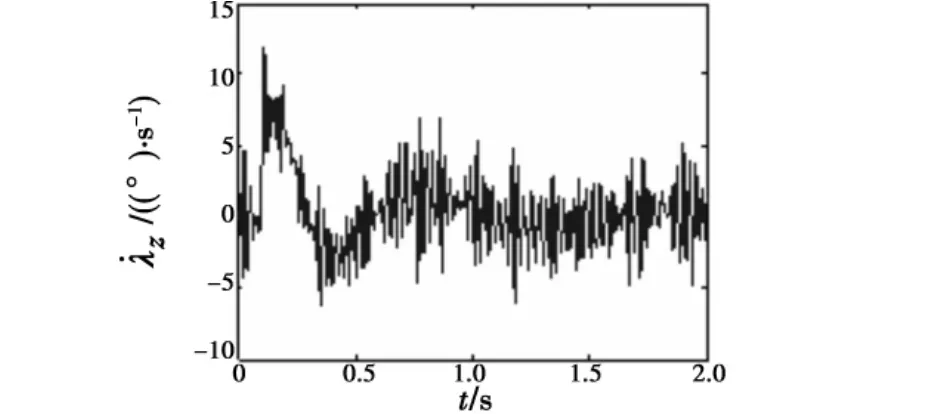
图12 框架角速度(俯仰通道)Fig.12 Gimbal angular rate(elevation)
4 结论
在捷联末制导系统中,导引头中取消了陀螺,天线稳定系统中所需的空间绝对角速度信息无法直接测量,此时可以利用弹上捷联惯导给出的弹体姿态运动信息,以及导弹、导引头、天线之间的相对运动关系,使用运动合成方法来重构天线空间运动信息,最终实现天线平台的间接稳定,这就是基于角速度补偿的捷联天线稳定方案。捷联天线稳定系统本质上是一种数学稳定平台,其核心是基于DSP的解算控制模块,它包括伺服系统校正网络、稳定回路反馈量计算、视线角速度估算3种功能。
因为导弹弹体同时存在俯仰、航向、滚动3个通道姿态运动,导引头天线伺服系统也同时进行俯仰、航向两个通道的运动,这样实际的天线空间运动合成关系就不能按照的简单关系来表示,需要根据坐标变换关系和运动合成原理通过数学解算来获取,同时用于制导的目标视线角速度信息也可以通过数学方法间接提取。
在理想条件下,当陀螺通道与测速环节的传递函数完全匹配时,捷联稳定方案可以获得与陀螺稳定方案完全等效的控制效果,但是实际的测速环节动态特性一般都比陀螺系统要快,所以需要设计适当的匹配滤波器来平衡二者特性。此外,捷联算法中需要对伺服框架角λ进行微分运算,这将会放大传感器的测量噪声,需要采用高精度低噪声的测角元件,对传感器输出进行滤波处理以克服噪声的影响。
[1]RUDIN R T.Strapdown stabilization for imaging seekers[R].AIAA-93-2660,1993:1-10.
[2]KENNEDY P J,KENNEDY R L.Direct versus indirect Line of Sight(LOS)stabilization[J].IEEE Trans on Control System Technology,2003,11(1):3-15.
[3]周瑞青,吕善伟,刘新华.捷联式天线平台的角跟踪系统设计[J].系统工程与电子技术,2003,25(10):1200-1202.
[4]周瑞青,吕善伟,刘新华.捷联式天线平台的稳定性研究[J].北京航空航天大学学报,2003,29(6):509-511.
[5]张聘义,祁载康,崔莹莹.一种匹配滤波方法在导引头捷联稳定平台中的应用研究[J].红外技术,2005,27(1):6-11.
[6]周瑞青,吕善伟,刘新华.弹载捷联式天线平台两种稳定实现方法的比较[J].系统工程与电子技术,2005,27(8):1397-1400.

