路径点包含安全两方计算问题的求解

姚清芳，林柏钢

（福州大学 数学与计算机科学学院，福建 福州 350108）

0 引言

自从姚期智[1]1982年首先通过“百万富翁命题”提出了安全两方计算问题，1987年戈德里克[2]等人又考虑了安全多方计算问题以来，安全多方计算也成为了国际密码学界研究的热点问题之一。但是因为效率的问题限制，采用通用解决方案解决某些具体的多方安全计算问题是不现实的，必须针对不同的应用对象研究高效的解决方案。

多方安全计算中集合点包含和几何点包含等方法都是近几年密码学研究的一个热点问题[3-4]。提出的路径点包含问题是多方安全计算中一个新的研究课题。主要研究如何安全计算特定条件下两条或者多条路径之间的公共路径关系，通过特殊编码把路径和集合对应起来，再利用集合的方法求出了两路径的公共路径。最后分析证明了新方案的安全性。

1 预备知识

1.1 连接运算

这里定义一种字符串连接运算Concat,设为C()∶

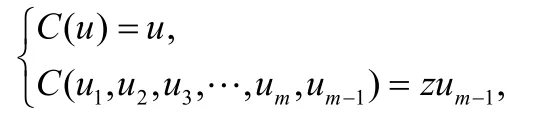
其中 z = C(u1, u2, u3,… ,um)，( u1, u2,u3,… ,um)为字符串集合；z=C(u1, u2, u3,… ,um)就是把字符串 ( u1, u2,u3,… ,um)一个跟着一个放在一起得到的新字符串。连接运算不仅保存了元素的信息还保存了元素间的顺序关系。

1.2 安全性考虑

提出的新方案都是建立在半诚实参与者基础上的。即，参与者在协议执行过程中严格地进行协议操作，但是他们会保留协议中的中间结果来推导其他参与者的输入。

安全性的定义：假设计算的双方是 A和 B。设f= ( f1,f2)是一个概率多项式时间函数，p是计算f的双方计算协议。当输入为(x,y)时，第 i方在执行协议中得到的信息序列viewi(x,y)为，v (x,y) = ( x,ri,, … ,mi)。其中ri表示

定义1 对于一个函数f，如果存在概率多项式时间算法S1,S2使得：

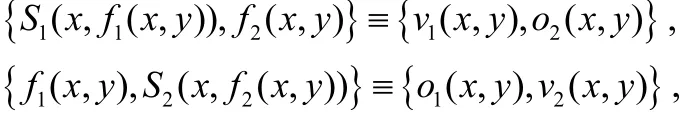
其中符号“≡”表示计算不可区分，则认为p保密地计算f。如果要证明一个方案是保密的，就必须构造出满足这个式子的模拟器S1,S2[5]。

2 新方案原理描述

问题描述：假设有两条路径 G1∶x1→ x2→…→xn，G2∶y1 → y 2→…→y m ，其中 ( x 1 , x2,… ,x n), (y1,y2,… ,ym)为路径上的点，箭头表示路径的方向。现在问题是需要计算出G1,G2的公共路径而不泄漏G1, G2的信息。

如图1所示，有两条路径G1∶A→C→F→H→Z，G2∶C→F →H→K→P ，需要安全的计算出G1, G2的公共路径C→F→H。

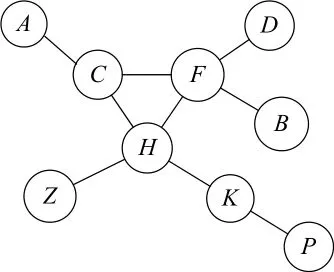
图1 G1, G2路径示意

2.1 基本思想

对路径进行特殊编码，把路径包含问题转化为集合包含问题，利用求集合交集得到两路径的公共路径。

2.2 问题分析

情形 1：G1,G2中任意两个点不相同，即每个点只经过一次

解决方案一：

①先对路径的点按照约定的规则进行数字化，对 G1,G2作如下编码：

这样A,B集合中的元素为G1,G2中所有长度为2的路径编码；

②连接运算。对A,B作连接运算：

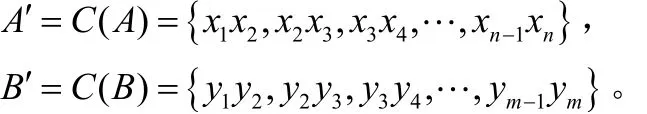
注意连接时，以最大值的位数为准，少于位数的补0，例如：最大值的位数为3，x1=20,x2=2, x1x2=02000。这样就确保了连接完编码的唯一性；

③利用集合交集的保密计算[4]：

A，B都得到： Eb( Ea(A′))和 Ea( Eb(B′))，A，B各自计算：C = Eb(Ea(A′))∩Ea(Eb(B′))，求出的C为G1,G2中所有长度为2的公共路径。因为每个点只经过一次，所以把C中头尾相等的点拼在一起即可求出G1,G2的所有公共路径。

情形2：G1,G2中每个点可经过多次。

解决方案二：

①先对路径的点进行数字化，然后编码如下：

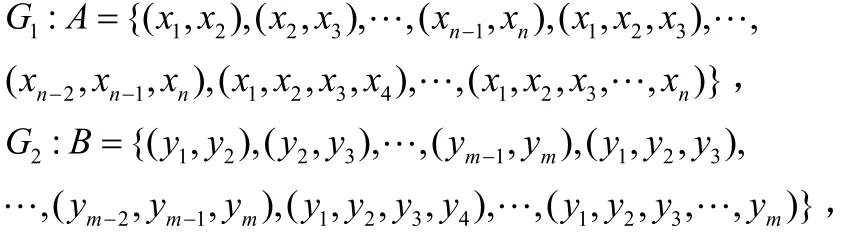
该编码实质是得到G1,G2中所有长度≥2的路径；

②同样对他们进行链接运算：

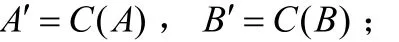
③因为位数太长了，所以对他们进行HASH运算：

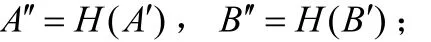
④利用集合交集的保密计算：

A,B都得到：Eb(Ea(A′))和Ea(Eb(B′))，

A,B各自计算：C = Eb(Ea(A′))∩Ea(Eb(B′))，C为G1,G2中所有长度≥2的公共路径。

情形3: G1,G2中点可以经过多次，但是只需求最长的公共路径

解决方案三：

当只需求两路径中最长的公共路径时，可以利用以下方案(方案三)减少时间复杂度。方案二中，把所有长度≥2的路径一次性全部拿去判断，这里进行了一些粗略的判断，例如当不存在长度为 k的公共路径时，就不必判断那些长度≤k的路径了。而方案三是在[1, min(n, m)]这个区间内利用二分思想进行交互，先交互长度为 m in(n, m)/2的路径，看看是否有，如果有则继续判断是否有长度为3·min(n,m)/4的路径；若没有的话，判断长度为 m in(n, m)/4的路径，就这样一直循环下去。这里的长度都需要取下整数。

循环停止的情况有两种，一种是求出的交集里面只有1个元素，这个时候该元素就为最长的公共路径；还有一种是取整完之后该长度的交集已经求过了，这个时候操作到了二分的终点，取最近求得的存在的长度路径。这样停止的时候就可以求出最长的公共路径。结果可极大的减少了时间复杂度，但是增加了通信复杂度。

2.3 性能分析

方案一中A,B集合的元素个数为n，编码、连接运算和集合交集保密计算的时间复杂度都是 O(n)，总共的时间复杂度为O(n)。通信复杂度是集合交集保密计算的通信复杂度为2。

方案二中因A,B集合中的元素个数为O(n2)，总共的时间复杂度为 O(n2)。通信复杂度也为 2。这里用到了 HASH运算，但是匹配错误的概率是可忽略的。

方案三中利用二分思想，时间复杂度可以由O(n2)降为O(n·log2n)，但是用到了O(log2n)次的交互，所以通信复杂度为O(log2n)。

综上所述，表1给出3种方案的时间复杂度和空间复杂度的比较。

表1 各方案的复杂度比较

在安全性方面，只要上述方案的零知识的，则方案的安全性等价于集合交集中所用的同态公钥体制的安全性，零知识的证明将在下面统一给出。

3 安全性证明

直观上看，因为A和B都不知道对方的密钥，都无法获得对方的路径信息，如果要知道对方的路径信息就必须获得对方的密钥，假定双方的密钥都是安全的，那么该方案就是保密的。下面针对方案一进行以下定理证明。

定理1 解决路径点包含两方问题的方案一是保密的。证明：证明的思路是通过构造模拟器S1,S2使得：

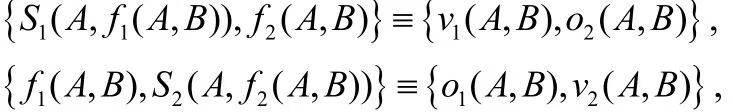
来证明方案的安全性。

在协议的执行过程中，A和 B观察到的过程与输出分别为：

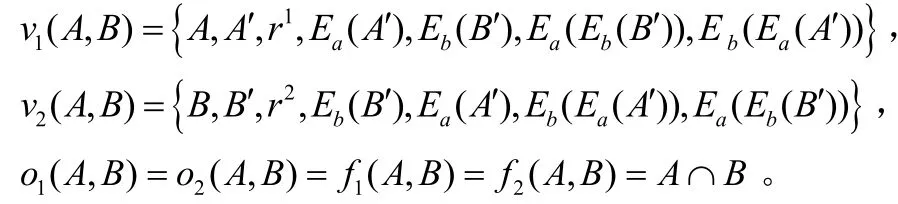
构造两个模拟器 S1,S2分别用于模拟 v1(A,B ) )和v2(A,B)。

首 先 构 造 S1， 使 得 ｛S1( A,f1( A,B ) ), f2(A,B ) ｝≡｛v1(A,B),o2(A,B ) ｝。

S1的模拟过程如下：

S1首先选择一个可交换加密算法 E和加密密钥 a,并根据硬币抛掷的结果 ( r1)′选择另一个密钥b′,根据A和B的公共路径C，生成一个新的路径对它进行编码使得 C中的元素与 D中前面的元素相等。对它进行连接运算得到的对A进行连接运算得到A′。

S1用a加密A′得到 Ea(A′),用 b′对 D′加密得到 Eb′(D ′)。

S1用a加密得到，再用b′对加密,得到

S1单独比较 Ea(′(D′))和′ ((A′))，根据前面构造A 和 D′的 方 法 ， 一 定 存 在 交 集 C 使 得，从而得出A∩B=C，C对应的路径集合为G1,G2的公共路径。.

不妨令：

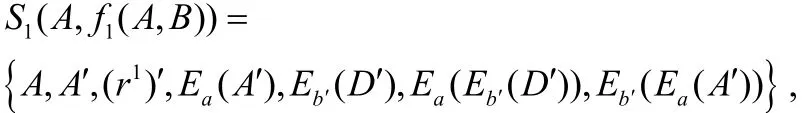
则有：

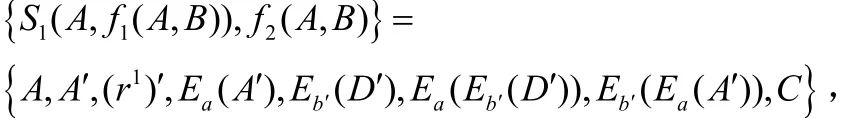
又因：

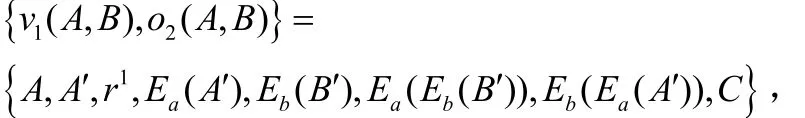
所以：

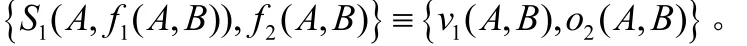
类似的可以构造一个模拟器 S2,使得：｛f1(A,B),S2( A, f2( A,B ) )｝ ≡｛o1(A ,B),v2(A,B)｝满足条件成立，这样就完成了定理的证明。同理，方案二、方案三的安全性证明类似方案一。

5 结语

针对路径点包含问题的两种不同的情况提出了几种解决方案，应用时可根据具体的应用环境选择方案。后续的工作可以围绕在不提高通信复杂度的情况下降低针对第二种情况下的时间复杂度，以及把两方计算扩展到多方计算，提出路径点包含安全多方计算的高效解决方案算法。

[1] YAO A. Protocols for Secure Computations[C]Los Alamitos: IEEE Computer Society Press, 1982:160-164

[2] GOLDREICH O,MICALI S,WIGDERSON A. How to Play ANY Mental Game[C].United States:ACM,1987:218-229.

[3] LUO Y L, HUANG L S, ZHONG H. Secure Two-party Point-circle Inclusion Problem[J].Journal of Computer Science and Technology,2007,22(01):88-91.

[4] 李顺东,司天歌,戴一奇. 集合包含与几何包含的多方保密计算[J].计算机研究与发展,2005,42(10):1647-1653.

[5] GOLDWASSER S. Multi-party Computations: Past and Present[D]Santa Barbara CA：[s.n.],1997.