地铁区间隧道速度场温度场特性研究

王丽慧 吴喜平 宋 洁 施 逵

(1 上海理工大学城市建设与环境工程学院 上海 200093；2 同济大学机械工程学院 上海 200092；3 上海申通轨道交通研究咨询有限公司 上海 202150；4 上海市隧道工程轨道交通设计研究院 上海 200070)

由于地铁车站环控热环境与人的舒适、健康及空调系统节能密切相关，因此，现有地铁热环境的研究多集中于此，即综合利用数值模拟[1]、现场实测[2]等研究方法，分析了地铁活塞风作用下，车站站台层、站厅层、出入口等单元速度场[3-4]、温度场[5-6]、压力场[7-8]的变化规律和空调系统能耗状况[9]等。而对于产生活塞风的地铁区间隧道，现有研究多见于以理论建模方式分析活塞风变化规律[10]，用现场实测方式分析隧道内壁温变化[11]，或用缩尺模型试验研究列车运行(最高时速125m/s)形成的隧道压力波[12]等。而对区间隧道内温度场、速度场热环境的总体综合分析较少。

地铁区间隧道热环境的重要性主要体现在如下两个方面：1)对闭式(开式)系统而言，对车站环控热环境有显著影响的活塞风产生于区间隧道，区间隧道内速度场和温度场的特性通过列车活塞风直接作用于车站环控，因此区间隧道热环境是影响车站舒适性和能耗的根本原因。2)对于屏蔽门系统，区间隧道速度场变化直接影响到屏蔽门所需承受的风压及漏风量，而区间温度变化情况是屏蔽门系统的重要关注指标。可见，对地铁区间隧道速度场、温度场的研究具有重要的理论价值和现实意义。

这里通过缩尺模型试验、现场监测和数值模拟等研究方法，分析地铁区间隧道速度场和温度场变化的基本规律。

1 研究方法

1.1 缩尺模型试验

搭建几何尺寸相似比为1:30的缩尺模型试验台作为实际复杂隧道的抽象代表，来研究区间速度场随列车运行的变化规律。一方面，隧道是影响闭式系统车站环控的活塞风发源地，同时隧道风速、风压的变化规律又能反映屏蔽门系统区间长期存在气流运动的基本特征；另一方面，通过此实验来分析活塞风风速随车速、阻塞比和列车长度变化的基本规律。

模型试验以重物下落的拉力作为模型列车前进的动力，模型区间隧道长33m，模型列车与隧道横截面积、长度的比例均按实际地铁相应比例设计[13]；通过方程分析法，整理得到如下三个相似准则数Fr，Eu和Re：

式中，μ —动力粘性系数，N.s/m2；l—外形尺寸，m； ρ —空气密度，kg/m3；Δp —压差，Pa。

其中，Fr准则数主要考虑重力作用，模型实验主要研究区间活塞风的受迫运动，其动力源于水平方向上的压力差，重力不起决定性作用，故Fr准则可不予考虑。在粘性流体受迫运动场合，考虑粘性力的雷诺准则Re对流动状态起决定性作用。通过计算，模型实验的雷诺数约为5.47×108，远大于粗糙管最大雷诺数临界值[14]9.5×105，模型试验区间内流体已进入第二自模区，故模型试验与实际隧道内的流体运动自动满足雷诺相似准则。

因此，缩尺模型试验设计需满足几何相似和欧拉准则数相似，而欧拉数中的空气密度ρ可认为模型与实物自动相等，压差Δp与车速相关[15]，气流速度v主要由列车运动产生，与车速密切相关，故必须保证模型列车的运行速度与实际地铁车速相近，这是满足模型相似性的必要条件，也是模型试验取得成功的关键。

通过调节重物质量，模型列车车速可达到与实际地铁车速接近的7m/s～13m/s。模型试验台原理图和实体图分别参见图1、图2。

图1 缩尺模型试验台原理图Fig.1 The schematic of scale model test

图2 缩尺模型试验台实体Fig.2 The photos from scale model test

1.2 现场监测

采用现场监测方法研究区间温度场主要基于以下两方面考虑：1)地铁区间热容量较大，难以通过模型试验再现区间温度场；2)狭长的地铁区间不利于人员安全、有效地进行多列车工况的现场实测。现场监测的具体方法是在上海地铁一号线某区间中部安装型号为PG100的温度传感器(仪器测试范围-40℃～50℃，测试精度±0.5℃)，通过区域控制器与车控室数字转换器相连，全天24小时工作，每隔15min自动记录温度实时监测数据。

1.3 SES数值模拟

Subway Environment Simulation(简称SES)是被国际上广泛认可的、相对成熟的地铁热环境模拟软件。其针对地铁热环境研发，经过了模型试验验证[16]，可准确模拟多工况下的地铁热环境变化。建立图3节点图数学模型，模拟对象为完整区间隧道，其临界条件选取和参数设定均依据地铁实际情况，基本参数选取见表1。其中节点(node)81～节点(node)87为下行线区间，段(section)81～86分别代表断面1～断面6，子节83-1～83-13对应断面3内等分的13个子断面。

表1 数值模拟各工况基本参数设定Tab.1 Fundamental parameters of each condition in SES

图3 地铁区间隧道单元的SES数学模型Fig.3 SES mathematical model in tunnel

2 研究内容与分析

2.1 区间速度场研究

2.1.1 缩尺模型试验研究结果

1)区间最大风速计算表达式

利用模型试验，在保证其他参数不变的情况下，通过调整下落重物的质量和列车车头的横截面积，特就最大车速为7m/s、10m/s和13m/s时，进行了不同阻塞比条件下的单因素试验，试验结果如图4所示。通过上述改变车速和阻塞比的模型试验得到，其反映的区间隧道最大风速vmax可由下式表示：

式中，v0—列车车速，m/s；l—隧道长度，m；l0—列车长度，m；β—列车对隧道的阻塞比。

图4 区间风速随车速和阻塞比变化的模型试验Fig.4 Tunnel velocity varied with v0 and β

2)区间断面最大风速的滞后性

由缩尺模型试验研究发现，列车前方某点最大风速与最大车速并不同时出现。称车速最大时该点的风速为即时风速，其往往小于最大风速，两者的比值随车速不同而变化。这是因为气流相比于车速的变化，在时间上有一定的滞后性。将区间内某点即时风速vx与最大风速vmax的比值用δ表示。模型试验数据拟合得到δ与车速v0的关系式(3)，试验数据及拟合曲线变化见图5。

图5 δ随车速变化的模型试验结果Fig. 5 δ varied with v0 in model test

从图中可见，δ随车速的增加而减小。而试验研究发现，地铁区间某点的最大风速往往出现在列车车尾通过该点时。

2.1.2 列车匀速运行工况

缩尺模型试验分别采用多点风速采样仪(测试精度为±0.01m/s)和微压计(测试精度为±0.1Pa)测试模型隧道风速与压力，测点每隔5m均匀布置，风速v和风压p试验结果见图6。

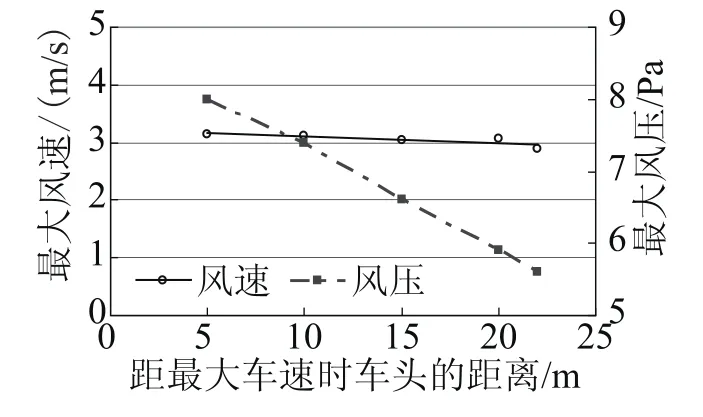
图6 模型试验车头前隧道风速与风压分布Fig.6 The tunnel velocity and pressure distribution

其中，模型试验中最大风压pmax随距车头距离x变化的试验数据可拟合得下式：

可见，由模型试验得到：列车匀速运行时，区间内列车前方各点风速不变；越靠近隧道出口，l'越小，p'压力越小。

根据图3的SES数学模型，当列车以15.6m/s的速度匀速运行时，隧道各断面风速变化的数值模拟结果见图7。

图7 列车匀速运行隧道内风速数值模拟结果Fig.7 The tunnel velocity with constant train speed

由图7知，数值模拟结果与缩尺模型试验结果一致，即列车匀速运行时，区间风速不变，验证了SES数学模型的正确性。

2.1.3 列车变速运行工况

区间内列车变速运行过程可分为列车进洞的加速过程(由部分列车进洞、全部列车进洞组成)和列车出洞的减速过程(分为部分列车出洞、全部列车出洞)。列车变速运行时，区间速度场随时间的变化规律是关注对象。现有的理论分析将区间风速表述成与时间有关的微分解析式，但风速随时间变化的规律不明显，现通过数值模拟深入研究。

1)列车加速进洞工况

图8(a)反映了列车进洞加速过程，区间隧道内各断面平均风速随时间的变化规律，拟合为：

表2 区间各断面拟合关系式(4)系数及相关系数Tab.2 The coef fi cient of formula 4

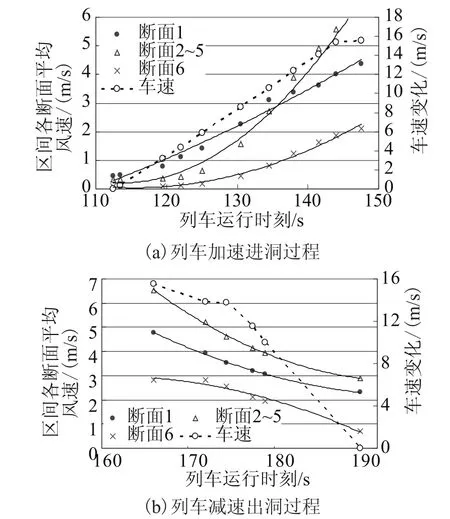
图8 列车变速工况，车速及区间风速随时间变化Fig.8 The tunnel velocity with changerable train speed

2)列车减速出洞工况

列车减速出洞过程，区间隧道各断面模拟结果见图8(b)，断面平均风速随时间拟合如下：

表3 区间各断面拟合关系式(5)系数及相关系数Tab.3 The coef fi cient of formula 5

2.1.4 区间速度场随时段与季节的变化

列车运行产生的活塞风是影响区间隧道速度场的主要因素，其累积效应体现在各季节不同时段区间速度场的不同。一方面，平均速度明显大于非高峰时段；另一方面，夏热冬冷地区，夏季、冬季地铁实行闭式运行，过渡季开式运行，活塞风井开启，区间隧道受活塞风影响的程度加大，故过渡季区间隧道内平均风速较冬季、夏季大。数值模拟结果符合上述分析的规律，见图9。

图9 区间不同时段风速比较的数值模拟Fig.9 The tunnel velocity comparison during times

2.2 区间温度场研究

列车运行产热是地铁内主要得热，占总得热量的70%～80%[17]。列车运行产热包括：列车表面空气阻力摩擦生热，车轮与钢轨间及车轮与轴承间摩擦生热，车内照明、空压机等辅助机械产热，以及列车空调冷凝器排热。列车前进过程中，这些热量一部分通过活塞风带到站台或由活塞风井排向室外，另一部分留在隧道内引起区间温度场的变化。在列车活塞风作用下，区间温度场随时间和列车位置发生变化。

2.2.1 区间温度场随时间的变化

以夏季闭式系统区间温度为研究对象，靠近站台的区间两端温度受车站空调系统影响较大，而区间隧道中部温变规律具有一定的代表性。全天24小时隧道中部气温现场监测结果见图10。此外，从图中可见，SES数值模拟得到的隧道中部平均温度随时间变化曲线与监测结果相似，验证了该数学模型研究区间隧道温度场的正确性。

图10 夏季区间隧道中部气温随时间变化的现场监测与数值模拟Fig.10 The middle tunnel temperature varied with time in summer

图11 地铁区间列车行车密度随时段的变化Fig.11 The train numbers varied with times

现场监测日选取在8月中旬，室外日最高气温33.3℃，隧道内部最高温度高出室外约3℃。由于监测段地铁投入运营时间较长，区间围护结构蓄热多、热容量大，区间温度最大值与最小值相差不大，约1℃左右。引起区间温度场变化的主要因素为室外温度和列车行车密度(其随时段变化参见图11)，分6个典型阶段分析区间气温变化规律。1)阶段I(6:00～7:00)：列车开始运行，区间内气温随列车运行散热和夏季室外气温升高而小幅上升。2)阶段II(7:00～9:00)：地铁客流早高峰时段，行车密度由4.6辆/小时增大到10.9辆/小时，列车在隧道内散热增大，虽然车站空调系统已开启，但隧道中部温度上升显著。3)阶段III(9:00～16:00)：一方面为夏季室外气温较高时段，区间温度有所升高；另一方面为地铁运行非高峰时段，行车对数减少，列车在隧道内释放热量减少，而活塞风又将一部分站台冷空气带入隧道。数值模拟中设定车站环控空调系统能够维持非高峰时段区间温度的稳定；而现场监测数据，因该区段地铁运营多年，区间围护结构散热量受室外温度影响明显，并与室外最高温度出现的时间存在延迟，约14:00区间温度最高。4)阶段IV(16:00～19:00)：地铁运行晚高峰时段，虽然室外温度下降较大，区间气温因列车散热量的增加而保持较高水平。5)阶段V(19:00～22:00)：非高峰时段且夏季室外温度较低，活塞风继续将站台冷空气带入隧道，区间隧道气温下降显著。6)阶段VI(22:00～次日6:00)：地铁区间内无列车运行，站台空调系统关闭，夏季夜晚室外气温较低，区间隧道温度在室外温度影响下缓慢下降。

2.2.2 区间温度场随列车位置的变化

由缩尺模型试验研究知，当列车车尾刚刚通过测点时，测点的纵向风速最大，此时风量所携带的列车放热量对该测点温度影响最显著。为分析区间隧道内各断面温度随列车位置的变化规律，选取不受站台环控空调系统影响的过渡季节，在SES数学模型中用13个子断面均分断面3所代表的区间段，各子断面的位置坐标见表4，各子断面温度随车头位置变化见图12。

表4 区段3内13个均分子断面的位置坐标Tab.4 The 13 sub-section locations in section 3

图12 各子断面温度随车头位置变化的数值模拟Fig.12 The sub-section temperature varied with train head

经曲线拟合得到，13个子断面平均温度t与车头位置坐标x均满足式(7)，13个子断面关系式中常数c1～c6的平均值及拟合相关系数平均值见表5。数学模型中车长140m，从表4和图12中温度最大值时的坐标比较得出，两者之差均为140m左右，即车尾刚刚通过断面时，该断面温度最高。

表5 区段3内13个子断面关系式各项系数平均值及平均拟合相关系数Tab.5 The average coef fi cient of the 13 formulas

2.2.3 隧道壁温变化特性

由理论分析，建立隧道衬砌表面吸(放)热量Qx(f)关系式：

式中，q —隧道衬砌表面热流密度，W/m2；τ —吸(放)热时间，s；ψ —对流换热系数，W/m2.℃；tn—隧道内空气温度，℃；tw—隧道壁温，℃；Sz—隧道内总表面积，m2；Sz=Bl，B—隧道周长，m；l—隧道长度，m。

当(tn-tw)＞0时，衬砌表面吸热；当(tn-tw)＜0，衬砌表面放热；在整个热交换时段内，平均温度取(tn-tw)/2=Δt/2，则列车通过隧道过程中，衬砌表面的总Qx(f)为：

式中，ΔQ—隧道内剩余热量，W；K吸—隧道壁面吸热系数，即：

其中，S—隧道横截面积，m2；γ—隧道内空气密度，kg/m3；C—空气重量比热容，J/kg.℃。

可见，隧道壁面吸热系数与隧道壁面对流换热系数、隧道周长与横截面积之比，壁面的吸放热时间等因素有关，其数值与活塞风速密切相关。若K吸≥1，即Qx(f)≥ΔQ，说明列车经过隧道时，剩余热量能被衬砌表面全部吸收；若K吸≤1，即Qx(f)≤ΔQ，说明列车经过隧道后，剩余热量未被衬砌表面全部吸收。隧道壁面非稳定动态传热过程是围护结构蓄冷蓄热效应的原因所在。由理论分析知，在地铁远期运行中(K吸＜1)，隧道内列车发热量不能被壁面全部吸收，导致各季节的隧道气温均高于隧道壁温；而过渡季活塞风井开启，活塞风速的增加使隧道壁面的对流换热系数和吸热系数均增大，促进热交换，使气温与壁温之差明显小于夏季和冬季。鉴于模拟对象为远期运行的地铁，隧道及土壤的蓄热量较大，与隧道内空气温差小，传热效果较差，SES数值模拟中，混凝土和土壤的热传导系数分别取5.084 W/(m2.K)和4.483 W/(m2.K)，混凝土和土壤的热扩散系数分别取0.00266m2/h和0.00279 m2/h。图13实测与模拟结果的比较验证了模拟结果的正确性，图14为各季节长期运行地铁隧道气温与壁温比较。

图13 夏季隧道平均壁温与气温变化的数值模拟与现场监测Fig.13 The comparison between tunnel wall and air temperature

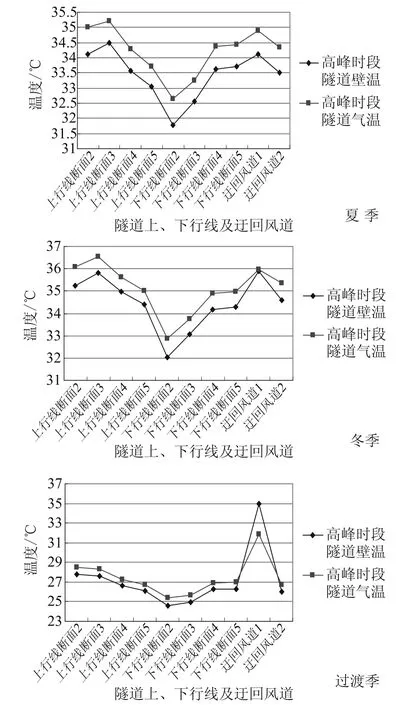
图14 各季节隧道各部分气温与壁温比较的数值模拟Fig.14 In different seasons the comparison between tunnel wall temperature and air temperature

3 结论

综合运用缩尺模型试验、现场监测和SES数值模拟等研究方法，分析了地铁区间速度场和温度场等热环境的基本规律，主要结论如下：

1)由缩尺模型试验研究得到，两端开口的区间隧道最大风速随车长、车速和阻塞比变化的表达式；区间风速相比于车速的滞后性与车速大小相关。

2)综合模型试验和数值模拟研究得到，两端开口的区间隧道内，列车匀速运行时，区间风速恒定，压力越靠近隧道出口处越低。由数值模拟得，列车加速进洞和减速出洞的变速运行过程中，区间各断面风速均随时间成二次函数变化关系。

3)区间速度场在隧道活塞风的作用下，高峰时段风速大于非高峰时段，且过渡季风速大于空调季。

4)结合数值模拟和现场监测数据，得到夏季区间隧道温度场全天24小时变化规律，在室外温度和行车密度两个主要影响因素作用下，可分为6个典型变化阶段。

5)拟合数值模拟研究结果，得到区间隧道温度场随列车位置的变化关系，列车车尾通过时，各子断面温度最高。

6)在理论分析基础上，通过现场监测与数值模拟得到，不同季节区间气温与壁温的相对变化趋势。

(本文受上海市教委重点学科建设项目(J50502)、上海高校选拔培养优秀青年教师科研专项基金(slg-07026)、上海市大学生创新活动项目(建筑能耗现场测试方法的实验研究)、上海市教委重点学科研究生创新基金(上海城市风场基本特性的研究)、上海理工大学博士启动经费项目资助。The project was supported by Project of Shanghai Municipal Education Commission(J50502), Special Research Fund in Shanghai Colleges and Universities to Select and Train Outstanding Young Teachers(slg-07026), University Student Innovative Project of Shanghai,Graduate Innovative Fund in Project of Shanghai Municipal Education Commission,the funds for Doctors in USST.)

[1]贾力, 黄鹏, 杨立新. 地铁车站内流动特性的数值模拟[J]. 北京交通大学学报,2008,32(1):83-87. (Jia Li,Huang Peng, Yang Lixin. Numerical simulation of flow characteristics in subway station[J]. Journal of Beijing Jiaotong University, 2008, 32(1): 83-87.)

[2]王丽慧, 吴喜平. 地铁活塞风对车站环控速度场的影响[J]. 地下空间与工程学报, 2007, 3(1): 161-166.(Wang Lihui, Wu Xiping. The affect on the subway system from the piston action wind[J]. Chinese Journal of Underground Space and Engineering, 2007, 3(1): 161-166.)

[3]Kim J Y, Kim K Y. Experimental and numerical analyses of train-induced unsteady tunnel flow in subway[J].Tunneling and Underground Space Technology, 2007,22(7): 166-172.

[4]那艳玲. 地铁车站通风和火灾的CFD仿真模拟与实验研究[D].天津：天津大学，2004.(Na Yanling. CFD simulation and experimental research on subway station ventilation and fi re[D]. Tianjin: Tianjin University, 2004.)

[5]Kazuhiro, Fukuyo. Application of computational fluid dynamics and pedestrian-behavior simulations to the design of task-ambient air-conditioning system of a subway station[J]. Energy, 2006,31:706-718.

[6]Ming Tsun Ke, Tsung Che Cheng. Numerical simulation for optimizing the design of subway environmental control system[J]. Building and Environment, 2002, 37:1139-1152.

[7]朱培根, 朱颖心. 地铁环控模拟与分析[J]. 地下空间, 2004,24(2) : 161-165. (Zhu Peigen, Zhu Yingxin.Subway environment simulation and analysis[J].Underground Space, 2004, 24(2) : 161-165.)

[8]荣莉, 马最良, 等. 侧式站台和岛式站台活塞风特性分析比较[J]. 建筑热能通风空调,2007,26(4) :86-89.(Rong Li, Ma Zuiliang, et al. Comparison of piston wind simulating analysis between different platforms[J].Building Energy & Environment. 2007,26(4) : 86-89.)

[9]江泳, 朱颖心. 地铁变风量空调节能潜力分析. 地铁与轻轨, 2002, 56(2): 31-32. (Jiang Yong, Zhu Yingxin.Subway VAV energy-saving potential analysis[J]. Urban Rapin Rail Transit, 2002,56(2) : 31-32.)

[10]沈翔, 吴喜平. 地铁活塞风特性的测试研究[J]. 暖通空调, 2005,35(3): 54-57.(Shen Xiang, Wu Xiping.Character testing of piston wind in a underground railway tunnel[J]. HV&AC. 2005,35(3): 54-57.)

[11]王树刚, 朱颖心. 北京地铁地下空间温度的测量与分析[J]. 地下空间, 2002,22(4) :339-343. (Wang Shugang,Zhu Yingxin. Measurement and analysis of temperature in underground space of beijing subway[J]. Underground Space, 2002,22(4) : 339-343.)

[12]高波. 高速列车进入隧道产生压缩波的数值模拟及试验研究[D]. 成都：西南交通大学, 2003.(Gao Bo. The experiment and numerical simulation on the pressure produced by a high-speed train entering into a tunnel [D].Chengdu: Southwest Jiaotong University, 2003.)

[13]王丽慧. 地铁活塞风与地铁环控节能[D]. 上海：同济大学, 2007. (Wang Lihui. The piston wind and the subway energy-saving[D]. Shanghai: Tongji University, 2007.)

[14]徐有恒，穆展. 基础流体实验[M]. 上海：复旦大学出版社，1990: 201. (Xu Youheng, Mu Zhan. Base fluid experiment[M]. Shanghai: Fudan University Press. 1990:201.)

[15]任明亮, 陈超, 郭强, 等. 地铁活塞风的分析计算与有效利用. 上海交通大学学报, 2008,42(8):1376-1381.(Ren Mingliang, Chen Chao, Guo Qiang. Numerical analysis and effectively using of piston-effect in subway. Journal of Shanghai Jiaotong University, 2008,42(8):1376-1381)

[16]SES Users Manual V41

[17]熊艳. 北京地铁内部环境状态数值模拟及分析[D]. 北京: 北京交通大学, 2004. (Xiong Yan. Beijing subway environment simulastion and analysis[D]. Beijing: Beijing Jiaotong University, 2004.)

[18]王秀英, 刘维宁, 等. 秦岭隧道内温湿度对作业人员的影响研究[J]. 北方交通大学学报, 1999, 23(4):26-29.(Wang Xiuying, Liu Weining, et al. Investigation about the effects of temperature and humidity on personnel in qinling railway tunnel[J]. Journal of Northern Jiaotong University, 1999, 23(4): 26-29.)