常幅循环荷载下岩石的变形特性

肖建清 ，丁德馨，徐根，蒋复量

(1. 中南大学 资源与安全工程学院，湖南 长沙，410083；2. 南华大学 核资源与安全工程学院，湖南 衡阳，421001)

工程中的岩体不仅仅承受着静态荷载的作用，还经受着爆炸、冲击、地震等动态荷载的影响。因此，研究循环荷载作用下岩石的疲劳特性，提出稳定性分析方法和控制手段是工程中迫切需要解决的问题。特别是近年来，由于大规模水利工程的建设，城市地下交通的普及，大跨度超长隧道的开挖，以及深部矿藏的开采，还有许多动力学问题需要研究。岩石是一种极不均质的天然地质材料，不同岩性的岩石具有不同的力学性能，即使是同一种岩性的岩石，由于其内部节理、裂隙等缺陷大量存在，其力学性能也呈现出较大的离散性，因此，对岩石材料疲劳试验的研究比对金属以及混凝土材料的研究都要困难得多。国内外研究者通过大量的试验研究取得了许多成果，获得了许多规律，例如岩石疲劳破坏的极限变形规律[1-2]、轴向变形的三阶段演化规律[1-4]、影响疲劳强度的因素[5-6]、加卸载塑性滞回演化规律[7-10]、疲劳破坏过程中材料性能劣化及微观裂纹演化规律[10-21]等。本文作者研究常幅循环加载条件下岩石的变形特性，除验证极限变形规律以及轴向变形3阶段演化规律外，还对横向变形以及体积变形进行研究和探讨，试图将微观裂纹和损伤演化与宏观变形3阶段规律建立对应关系。

1 试验设备及方法

试验采用的花岗岩取自衡阳县井头镇，其组分主要有：石英、斜长石、黑云母以及钾长石。为了提高试验的可对比性，避免由于深度不同造成的岩样内部微观结构的显著差异，用于制备试样的岩块取自同一岩层的相邻部位，同一组试样是通过密集套钻的方式在同一块岩石上取得。将试样加工成直径为50 mm、高100 mm的标准圆柱形，端面的平行度控制在±0.02 mm以内。

静态试验以及疲劳试验在 RMT-150B岩石力学测试系统上完成。RMT-150B是由中科院武汉岩石力学研究所研制开发的多功能液压伺服试验系统，可以完成岩石的单轴、三轴压缩试验，以及岩石节理面的直剪试验和间接拉伸试验。该系统具有稳定性好、响应快、精度高、操作方便、一机多用的特点。

静态试验采用载荷控制，加载速率为0.1 kN/s，共使用了6个试样，测得的平均抗压强度为143.43 MPa。疲劳试验也采用载荷控制，加载分2个阶段：第1阶段以等速率0.1 kN/s从零加载到平均荷载；第2阶段以平均荷载为起点，施加周期性荷载。疲劳加载时加载波形统一使用正弦波，频率为0.2 Hz。

2 极限变形规律

实验研究表明：对于岩石材料，即便是严格按照国际标准制备试样，保证加载条件，环境的温度和湿度不变，得到的疲劳寿命仍然具有较大的离散性。因此，在应力空间建立岩石的疲劳破坏准则非常困难，而葛修润等[1-2]发现：岩石疲劳破坏时(破坏点)的极限变形保持相对稳定，而且这一极限变形量与静态全过程曲线破坏后区对应上限应力处(控制点)的变形量相当，从变形的角度建立岩石的破坏准则似乎更可靠。

图1所示为疲劳加载曲线与静态全过程曲线的关系。可见：控制点C与破坏点F的应变几乎相等。

表1列出了本文所有试样的试验结果。从表1可以看出：应变相对偏差不超过13.00%，极限应变比较稳定。

图1 疲劳加载曲线与静态全过程曲线的关系Fig.1 Relationship between fatigue and static stress-strain curves

3 轴向变形演化规律

图2所示为试样F1-7的应变演化曲线，对应的轴向应变速率演化曲线如图3所示。从图2和图3可见：轴向应变演化以及轴向应变速率演化曲线都具有3阶段发展规律。文献[1-4]也给出了相同的结论，并将曲线划分为初始阶段、等速阶段和加速阶段。在图2中：在初始阶段，曲线上凸，变形发展较快；在等速阶段，曲线以恒定速率呈线性规律发展；在加速阶段，曲线上凹，轴向应变急剧攀升，在很少的几个循环内轴向应变迅速增至疲劳破坏的极限应变值。从图3还可以看到：在初始阶段，应变速率逐渐降低，然后过渡到应变速率近乎为0的等速阶段；进入加速阶段后，应变速率迅速增长，岩石发生失稳破坏，3阶段规律非常明显。

岩石轴向变形的3阶段发展规律是岩石微观损伤演化的综合体现。虽然国内外研究者对岩石微细观损伤方面进行了研究和探讨，但没有系统总结归纳。

表1 试样疲劳破坏时的极限应变Table 1 Ultimate strain to failure under fatigue loading for samples

图2 试样F1-7的轴向应变演化曲线Fig.2 Evolution curve of axial strain of specimen F1-7

图3 试样F1-7的轴向应变速度演化曲线Fig.3 Development curve of axial strain rate of specimen F1-7

从本质上说，岩石在循环荷载作用下发生疲劳破坏是岩石内部微裂纹萌生、扩展、直到贯通的动态演化过程。相应地，其内部微裂纹和损伤的发展亦可划分为3个阶段：第1阶段为岩石内部微裂纹形成阶段。在这一阶段，由于内部原生裂纹、微孔洞、颗粒边界等薄弱环节的存在，随着循环次数的增加，在这些薄弱环节处迅速产生大量微裂纹，这表现在开始几个循环时，岩石的轴向变形发展较为迅速。文献[11]中细观试验结果表明，局部裂纹的萌生表现出明显的矿物类别的选择性，石英颗粒边界较长石和黑云母更易萌生裂纹，矿物颗粒的力学性能较原生裂纹的几何尺寸及取向更加显著地影响着局部破坏的发生。随着循环次数的进一步增加，每次循环形成的微裂纹数目逐渐减少，同时，由于其中一部分裂纹以及矿物颗粒的阻裂作用，迫使岩石的应变增长速率也逐渐降低，岩石内部薄弱区形成微裂纹的过程趋于完成。此后，岩石的疲劳循环进入占疲劳寿命绝大部分的第2阶段。在这一阶段，岩石的轴向变形以及岩石的总孔隙率都随着循环次数的增加而稳定增加，已形成的裂纹处于稳定扩展阶段；随着循环次数逐步增加，裂纹进一步变长变宽，当裂纹达到一定的临界长度时，裂纹发生不稳定扩展而迅速贯通，岩石发生脆性破坏，这是第 3阶段。微裂纹的萌生、稳定扩展、失稳扩展3个阶段演化规律正是岩石变形3阶段演化规律的根源。

4 横向变形演化规律

常幅疲劳荷载作用下岩石的应力-横向应变曲线如图4所示。从图4可以看出：随着循环次数的增加，滞回曲线呈疏—密—疏的变化规律，逐渐向应变轴倾倒。蒋宇等[3]认为在每个加、卸载循环过程中，横向应变的发展和恢复都很小，滞回曲线以近乎直线的形式平行于纵轴发展，即使在临近破坏时也没有大的滞回环出现。作者考察了15个常幅疲劳试验，图4所示为典型的应力-应变曲线。从图 4可见：横向滞回环并非十分微小，在疲劳加载的中后期，其面积甚至超过了轴向滞回环的面积。图5所示为试样F1-7轴向和横向应变演化曲线。从图5可以看出：横向应变也具有3阶段发展规律，并非蒋宇等[3]提出的2阶段发展规律。而且，横向应变的3阶段规律比轴向应变的明显，各阶段的应变速率也要高一些。为了进一步论证横向应变在进入加速阶段前具有2个不同的阶段，再考察1个特殊试样。图6所示为试样F1-8的轴向和横向应变演化曲线。由图6可见：F1-8由于上限应力过低，循环数万次后仍未破坏，轴向最大应变几乎不变，处于等速发展阶段；在进入加速阶段前岩石的横向应变明显存在2个不同的阶段。

将F1-7的轴向应变放大，结果如图7所示。可见：轴向应变的3阶段划分与横向应变3阶段的划分基本一致。直线a和b将应变演化曲线截为3段：左边的称为初始阶段，中间为等速阶段，右边为加速失稳阶段。

图4 试样F1-7的应力-应变曲线Fig.4 Stress-strain curves of specimen F1-7

图5 试样F1-7的轴向和横向应变演化曲线Fig.5 Axial and lateral strain evolution curves of specimen F1-7

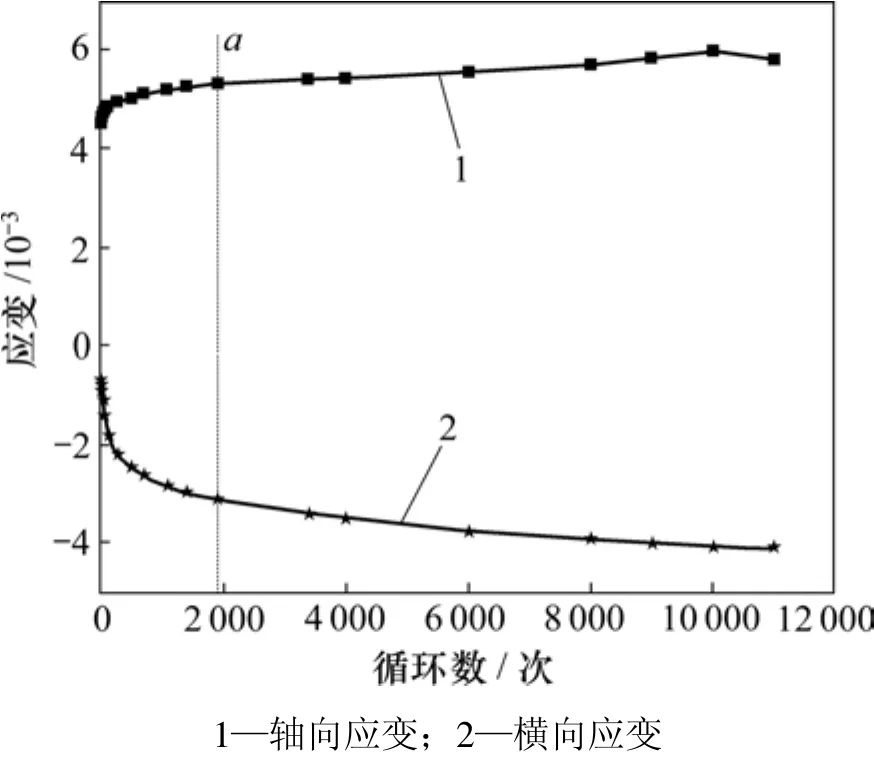
图6 试样F1-8的轴向和横向应变演化曲线Fig.6 Axial and lateral strain evolution curves of specimen F1-8

在进行疲劳加载之前，岩样有一段静态加载过程。在此过程中，岩石经历了原生裂纹的闭合以及微裂纹的萌生过程，轴向变形已达到了较高的水平。由于岩石是一种脆性材料，因此，在其后的循环加载阶段，其轴向变形非常有限。在单轴加载条件下，圆柱形试样的周边为自由面，轴向的压缩必然引起周向扩张，而循环加载中微裂纹的萌生以及扩展亦会导致岩石体积膨胀。而端部由于摩擦等因素的影响处于复杂三向受力状态，周向的扩张非常小，从而，加载过程中，绝大部分的扩容量挤向中截面。因此，在循环加载过程中，横向变形增量比轴向变形增量大得多，这也就导致最终的柱状劈裂破坏形态形成。

图7 试样F1-7的应变演化曲线3阶段划分Fig.7 Division of strain evolution curves of specimen F1-7

5 体积变形演化规律

岩石的应力-体积应变曲线如图8所示。从图8可见：直线a将曲线截为2部分，左边是体积应变小于0的情形，右边是体积应变大于0的情形。体积应变大于0表示试样的体积被压缩，小于0则表示体积发生膨胀，等于0代表体积保持不变。因此，若以未加载前的体积为参考，在前面的静态加载阶段以及很长一段时间的疲劳加载阶段，岩石一直处于体积压缩状态，只有临近失稳阶段后才出现体积膨胀的现象。若以体积压密的最小点C为参考，则每一次循环的体积应变都增长。蒋宇等[3]认为由于施加循环荷载前应力已经加到门槛值以上(葛修润等[12]证明，门槛值就是体积压密的最小点，即C点)，因此，整个循环过程中体积应变一直保持增长。事实上，疲劳加载的起点是图8中平均应力所处位置(S点)，虽然上限应力(M点)超过了门槛值，但S点却在体积压密最小点(C点)以下。因此，本文作者认为：在疲劳加载过程中，体积应变相对于体积压密最小点来说，一直保持增长。

若以上限应力对应的体积应变作为当前循环下的体积应变，则岩石的体积应变演化曲线如图9所示。从图9可以看到：岩石体积一直朝着膨胀的方向发展，体积应变发展曲线明显具有3阶段演化规律，与轴向应变和横向应变发展的3阶段相重合。在初始阶段，体积应变减小得比较快，这一变化在有限的几个循环中便已完成；随后进入等速阶段，体积应变发展速率几乎为一常数(负斜率)；到了加速阶段，体积应变迅速减小，直到岩石破坏。

图8 试样F1-7的应力-体积应变曲线Fig.8 Stress vs. volumetric strain curve of specimen F1-7

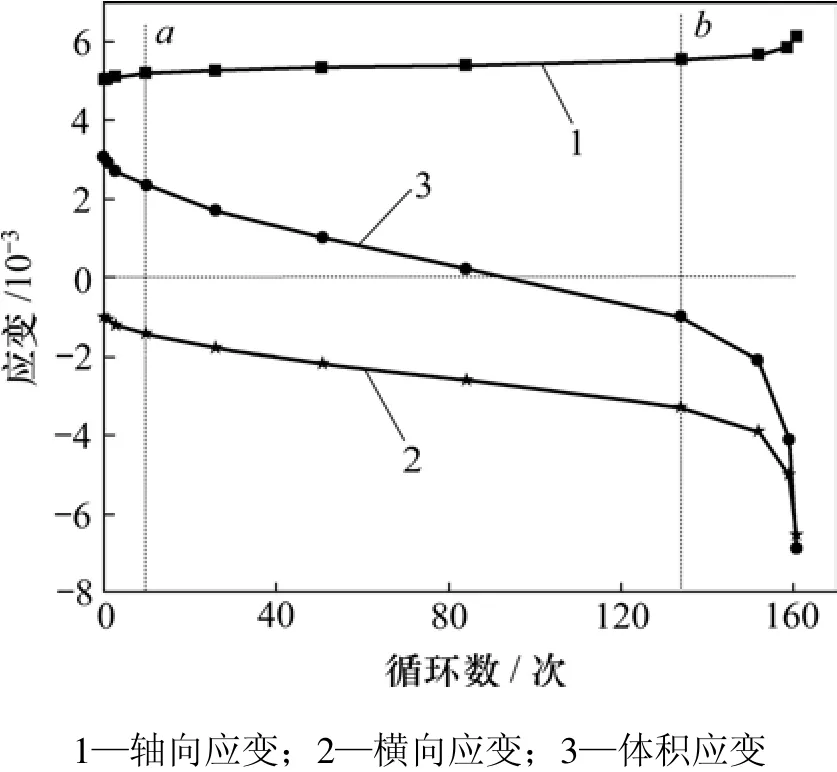
图9 试样F1-7的应变演化曲线Fig.9 Strain evolution curves of specimen F1-7

体积应变是轴向应变以及横向应变的综合体现。试验中横向应变测量的是中截面处的应变，因此，横向应变以及体积应变代表的都是危险点处的应变。

图10所示为3种应变的速率演化曲线。可见：横向应变速率介于轴向应变速率和体积应变速率之间。由于工程中难以直接测量体积变形，因此，采用横向变形或横向变形速率作为岩石疲劳破坏或失效的判据比较合适。

图10 试样F1-7的应变速率演化曲线Fig.10 Strain rate evolution curves of specimen F1-7

6 结论

(1)岩石疲劳破坏时的极限变形保持相对稳定的数值，而且这一极限变形量与静态全过程曲线破坏后区对应上限应力处的变形量相当，验证了极限变形规律，两者的相对偏差不超过13%，因此，从变形的角度建立岩石的疲劳破坏准则更为可靠。

(2)在循环荷载作用下，岩石的轴向应变、横向应变和体积应变都具有3阶段演化规律，3阶段的划分基本一致。

(3)横向应变的 3阶段规律比轴向应变的明显，横向应变速率亦大于轴向应变速率；因此，采用横向变形或横向变形速率作为岩石疲劳破坏或失效的判据，更有利于工程应用。

[1]葛修润, 蒋宇, 卢允德, 等. 周期荷载作用下岩石疲劳变形特性试验研究[J]. 岩石力学与工程学报, 2003, 22(10):1581-1585.GE Xiu-run, JIANG Yu, LU Yun-de, et al. Testing study on fatigue deformation law of rock under cyclic loading[J]. Chinese Journal of Rock Mechanics and Engineering, 2003, 22(10):1581-1585.

[2]章清叙, 葛修润, 黄铭, 等. 周期荷载作用下红砂岩三轴疲劳变形特性试验研究[J]. 岩石力学与工程学报, 2006, 25(3):473-478.ZHANG Qing-xu, GE Xiu-run, HUANG Ming, et al. Testing study on fatigue deformation law of red-sandstone under triaxial compression with cyclic loading[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(3): 473-478.

[3]蒋宇, 葛修润, 任建喜. 岩石疲劳破坏过程中的变形规律及声发射特性[J]. 岩石力学与工程学报, 2004, 23(11):1810-1814.JIANG Yu, GE Xiu-run, REN Jian-xi. Deformation rules and acoustic emission characteristics of rocks in process of fatigue failure[J]. Chinese Journal of Rock Mechanics and Engineering,2004, 23(11): 1810-1814.

[4]葛修润, 卢应发. 循环荷载作用下岩石疲劳破坏和不可逆变形问题的探讨[J]. 岩土工程学报, 1992, 14(3): 56-60.GE Xiu-run, LU Ying-fa. Study on fatigue failure and irreversible deformation of rock under cyclic loading[J]. Chinese Journal of Geotechnical Engineering, 1992, 14(3): 56-60.

[5]任建喜, 蒋宇, 葛修润. 单轴压缩岩石疲劳寿命影响因素试验分析[J]. 岩土工程学报, 2005, 27(11): 1282-1285.REN Jian-xi, JIANG Yu, GE Xiu-run. Test and analysis on rock fatigue life due to affecting factors under uniaxial compression[J]. Chinese Journal of Geotechnical Engineering,2005, 27(11): 1282-1285.

[6]Bagde M N, Petroš V. Fatigue properties of intact sandstone samples subjected to dynamic uniaxial cyclical loading[J].International Journal of Rock Mechanics and Mining Sciences,2005, 42(2): 237-250.

[7]许江, 杨秀贵, 王鸿, 等. 周期性载荷作用下岩石滞回曲线的演化规律[J]. 西南交通大学学报, 2005, 40(6): 754-758.XU Jiang, YANG Xiu-gui, WANG Hong, et al. Evolution law of hysteresis curve of rock under cyclic loading[J]. Journal of Southwest Jiaotong University, 2005, 40(6): 754-758.

[8]席道瑛, 陈运平, 陶月赞, 等. 岩石的非线性弹性滞后特征[J].岩石力学与工程学报, 2006, 25(6): 1086-1093.XI Dao-ying, CHEN Yun-ping, TAO Yue-zan, et al. Nonlinear elastic hysteric characteristics of rocks[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(6): 1086-1093.

[9]陈运平, 王思敬, 王恩志. 岩石应力-应变滞后现象的定量研究[J]. 岩石力学与工程学报, 2007, 27(增刊2): 4066-4073.CHEN Yun-ping, WANG Si-jing, WANG En-zhi. Quantitative study on stress-strain hysteretic behaviors in rocks[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 27(Suppl. 2):4066-4073.

[10]席道瑛, 王春雷, 田象燕. 滞回曲线对应力振幅和频率的响应[J]. 物探化探计算技术, 2001, 23(2): 121-124.XI Dao-ying, WANG Chun-lei, TIAN Xiang-yan. The responses of hysteresis loops to stress amplitude and frequency[J].Computing Techniques for Geophysical and Geochemical Exploration, 2001, 23(2): 121-124.

[11]李炼, 徐钺, 李启光, 等. 花岗岩板渐进破坏过程的微观研究[J]. 岩石力学与工程学报, 2001, 21(7): 940-947.LI Lian, XU Yue, LI Qi-guang, et al. Progressive cracking of granite plate under uniaxial compression[J]. Chinese Journal of Rock Mechanics and Engineering, 2001, 21(7): 940-947.

[12]葛修润, 任建喜, 蒲毅彬, 等. 岩石疲劳损伤扩展规律 CT 细观分析初探[J]. 岩土工程学报, 2001, 23(2): 191-195.GE Xiu-run, REN Jian-xi, PU Yi-bin, et al. Primary study of CT real-time testing of fatigue meso-damage propagation law of rock[J]. Chinese Journal of Geotechnical Engineering, 2001,23(2): 191-195.

[13]许江, 大久保誠介, 鲜学福. 循环载荷对三城目安山岩变形特性的影响[J]. 重庆大学学报: 自然科学版, 2000, 23(6):38-41.XU Jiang, Okubo S, XIAN Xue-fu. Effect of the circulate loading on the deformation of Sanjome Andesite[J]. Journal of Chongqing University: Natural Science Edition, 2000, 23(6):38-41.

[14]席道瑛, 刘云平, 刘小燕, 等. 疲劳载荷对岩石物理力学性质的影响[J]. 岩土工程学报, 2001, 23(3): 292-295.XI Dao-ying, LIU Yun-ping, LIU Xiao-yan, et al. Influence of fatigue loading on physical mechanical characteristics of rock[J].Chinese Journal of Geotechnical Engineering, 2001, 23(3):292-295.

[15]樊秀峰, 简文彬. 砂岩疲劳特性的超声波速法试验研究[J].岩石力学与工程学报, 2008, 27(3): 557-563.FAN Xiu-feng, JIAN Wen-bin. Experimental research on fatigue characteristics of sandstone using ultrasonic wave velocity method[J]. Chinese Journal of Rock Mechanics and Engineering,2008, 27(3): 557-563.

[16]Heap M J, Faulkner D R. Quantifying the evolution of static elastic properties as crystalline rock approaches failure[J].International Journal of Rock Mechanics and Mining Sciences,2008, 45(4): 564-573.

[17]LI G, Moelle K H R, Lewis J A. Fatigue crack growth in brittle sandstones[J]. International Journal of Rock Mechanics and Mining Science & Geomechanics Abstracts, 1992, 29(5):469-477.

[18]ZHANG Ping, LI Xi-bing, LI Ning. Strength evolution law of cracked rock based on localized progressive damage model[J].Journal of Central South University of Technology, 2008, 15(4):493-497.

[19]ZHANG Ping, XU Jian-guang, LI Ning. Fatigue properties analysis of cracked rock based on fracture evolution process[J].Journal of Central South University of Technology, 2008, 15(1):95-99.

[20]YE Zhou-yuan, HONG Liang, LIU Xi-ling, et al. Constitutive model of rock based on microstructures simulation[J]. Journal of Central South University of Technology, 2008, 15(2): 230-236.

[21]LI Xi-bing, ZUO Yu-jun, WANG Wei-hua, et al. Constitutive model of rock under static-dynamic coupling loading and experimental investigation[J]. Transactions of Nonferrous Metals Society of China, 2006, 16(3): 714-722.