基于离散小波变换的时变结构物理参数识别

王超，任伟新，黄天立

(中南大学 土木建筑学院，湖南 长沙，410075)

时不变模型可以用来描述许多结构系统的动力学特性，目前，许多研究主要针对于线性时不变结构系统的正问题和反问题。然而，许多实际的土木工程结构在其运营过程中表现出时变特性，例如列车过桥时桥梁的振动、结构发生损伤导致刚度退化等，结构参数(刚度、阻尼和质量等)会随时间发生变化。因此，识别这类结构的时变特征参数对监测结构运营状况和诊断结构损伤情况具有实际意义。对于时变结构模态参数识别，近年来许多研究人员提出了多种方法，如：续秀忠等[1-2]提出了用时频分析和非平稳时间序列的时变自回归建模的方法进行时变结构模态参数的识别；Liu等[3-4]提出了子空间识别方法，并建立了一个轴向移动悬臂梁试验来验证所提出的方法；庞世伟等[5]提出了基于整体数据子空间方法的改进算法，增强子空间算法的抗噪性；吴日强等[6]提出了一种适于在线跟踪的改进子空间算法；Hou等[7-8]提出基于连续小波变换的方法识别结构瞬时模态参数；Tsatsanis等[9]用ARMAX模型来描述时变系统，将时变系数用小波基函数展开，通过最小二乘法识别时变系统。因此，模态参数识别相对成熟。然而，对于时变结构物理参数识别的研究还较少。Shi等[10]提出了Hilbert变换和经验模式分解(EMD)的方法用于时变系统识别。Ghanem 等[11]运用小波伽辽金方法分析时变结构；Cooper等[12-13]提出了不同的自适应遗忘因子在线最小二乘法识别结构物理参数；李会娜等[14]提出了一种基于自由响应信号的时变结构物理参数子空间识别方法；任宜春等[15]提出了基于离散小波变换的识别方法。由于时变问题的复杂性，已提出的方法还未在实际工程中广泛运用，还有待更深入研究。本文作者将时变结构的时变参数离散化，利用离散小波变换将其在多尺度上展开为概貌信号和细节信号，选择合适的小波基函数使展开的信号能量尽量集中在低频区段，忽略高频细节信号，仅由低频概貌信号估计时变参数，将时变结构识别问题转化为时不变问题。通过最小二乘法识别出低频尺度展开系数，从而重构得到原始时变参数。用提出的方法对1个2层框架结构的时变刚度和阻尼进行有效识别。

1 信号多尺度小波分析

多尺度分析[16](也称为多分辨率分析)建立在函数空间概念上，将空间L2(R)进行逐级二分解产生一组逐级包含的子空间：

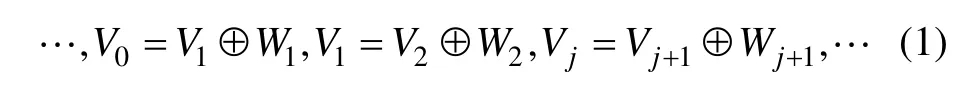
式中：Vj为尺度空间；Wj为小波空间，j∈Z。

对于任意平方可积函数x(t)∈L2(R)，将其向不同尺度的尺度空间和小波空间投影，可以在不同分辨率下对信号进行分析。若将x(t)按以下空间组合：

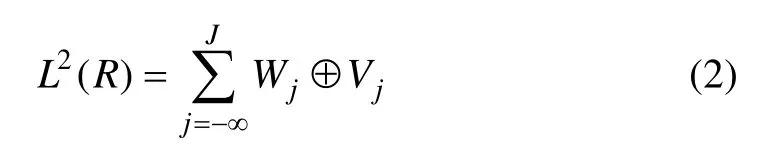
展开，可以得到函数x(t)的多尺度正交分解：

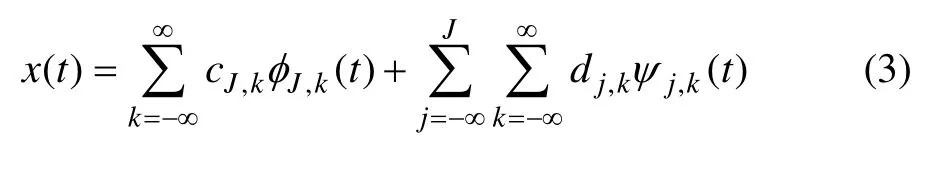
式中：cJ,k为第J尺度的尺度展开系数(也称为x(t)在分辨率J下的离散逼近)；φJ,k(t)为离散小波变换的尺度函数；dj,k为第j尺度的小波展开系数；ψj,k(t)为离散小波变换的小波函数。

多尺度分析可以通过滤波器组来计算。假定h0和h1分别为小波分解对应的低通和高通滤波器冲击响应，g0和g1分别为小波重构对应的低通和高通滤波器冲击响应，尺度系数和小波系数可以用Mallat塔式算法进行快速计算：

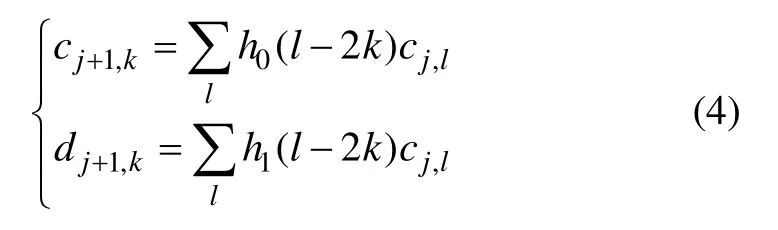
相应的系数重构算法为：

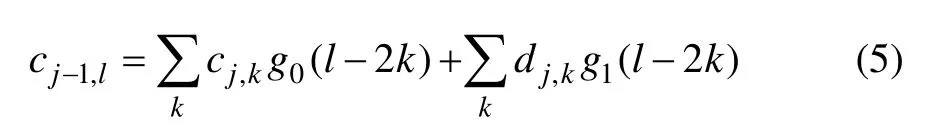
图1所示为2层多尺度小波分析原理。当信号采样频率大于Nyquist频率时，通常直接用x(t)的采样序列x(n)近视作为信号在0尺度分解上的尺度系数c0,k，则离散信号x(n)的J尺度分解和重构可由图1所示的滤波器组实现(仅表示了J=2层分解的情况)。图1中H0(Z)为分解低通滤波器h0(-n)的Z变换；H1(Z)为分解高通滤波器h1(-n)的Z变换；G0(Z)为重构低通滤波器g0(n)的Z变换；G1(Z)为重构高通滤波器g1(n)的Z变换；x′(n)为重构的信号。

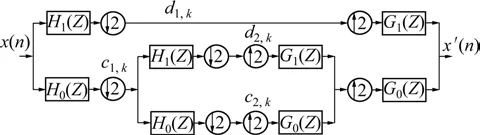
图1 2层多尺度小波分析原理Fig.1 Multiresolution analysis to depth of J=2

图2所示为等效分解和重构滤波器结构。由多采样率分析中的等效易位关系，图1所示的分解重构结构可以用图2所示结构等效。图2中：H(Z2)表示对传递函数H(Z)进行二插值。

对于信号J层分解，共有J+1个滤波器，其中低频部分的滤波器传递函数为：

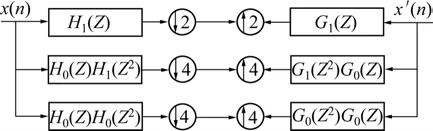
图2 等效分解和重构滤波器结构Fig.2 Equivalent decomposition and reconstruction filter structure

相应地，高频部分的滤波器传递函数为：

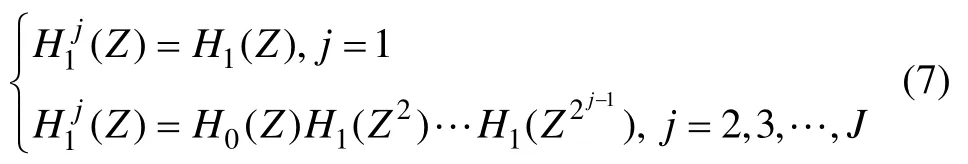
对于信号重构，相应的滤波器只需把式(6)和式(7)中的H改为G即可。令g0J(n)和g1j(n)分别为G0J(Z)和G1j(Z)的反Z变换，对信号进行J层分解，设分解的尺度系数和小波系数分别为cJ,k和dj,k，则离散信号x(n)可展开为：

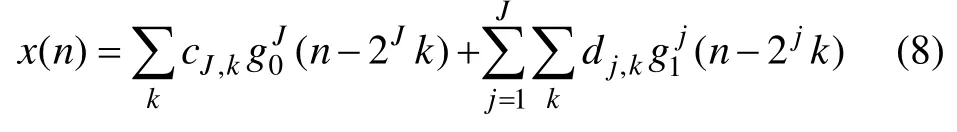
式中：k为分解小波系数的长度，与信号长度和分解层数相关。

2 时变结构物理参数识别方法

考虑单自由度时变结构系统，其质量为m，刚度和阻尼在振动过程中随时间缓慢变化，表示为c(t)和k(t)，对应的振动运动方程为：

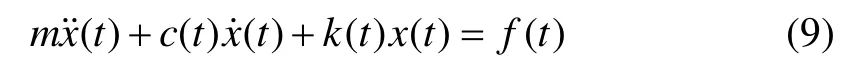
其相应的离散形式为：

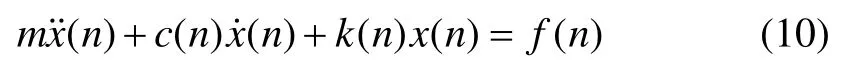
将时变阻尼和刚度看作一离散时间序列信号，设其J层小波分解的小波系数和尺度系数已知，根据式(8)将其展开。对于慢变信号，信号能量大部分集中在低频部分，展开时可忽略第2项细节信号，仅由第1项概貌信号来近似表示：

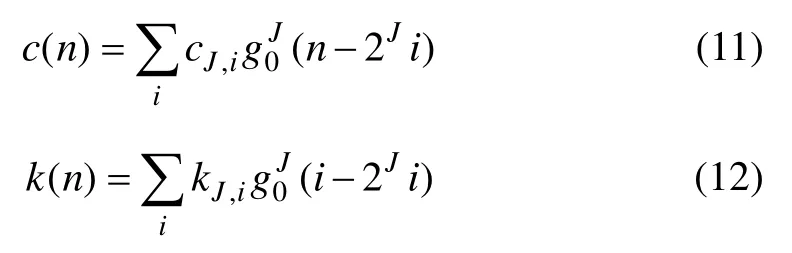
将式(11)和(12)代入方程(10)可得：

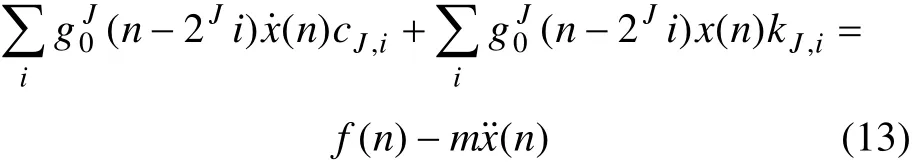
将所有离散时刻n=1～N的响应代入式(13)：

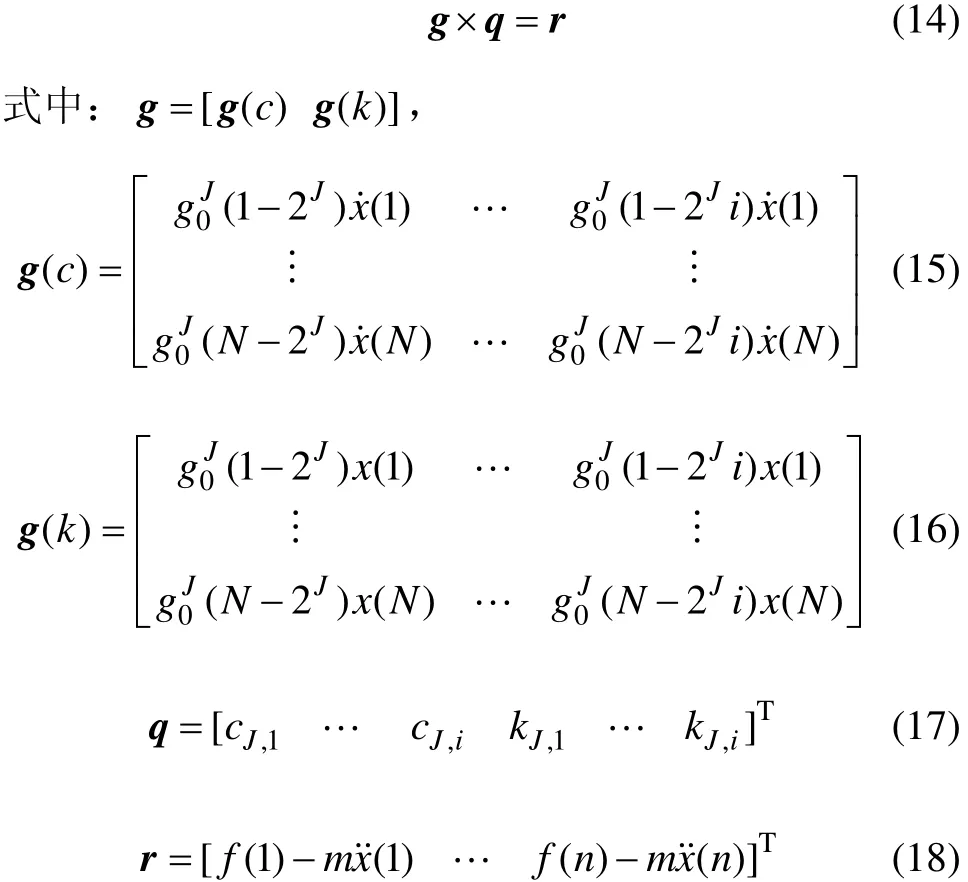
由最小二乘法可求出：

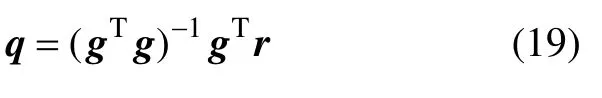
将式(19)求出的结果代入式(11)和(12)可求出结构的时变阻尼和时变刚度。

图3所示为2层剪切框架模型。对于多自由度时变结构系统，不失一般性，这里考虑如图3所示的2层剪切框架，各层刚度和阻尼时变，其振动方程为：

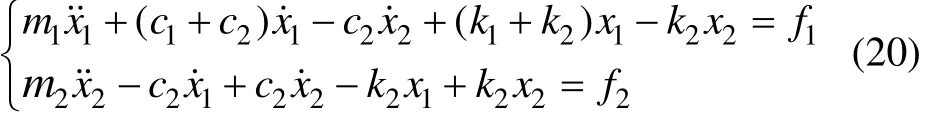
将刚度和阻尼作为未知量，把相同阻尼和刚度的系数移到一起，方程变为：

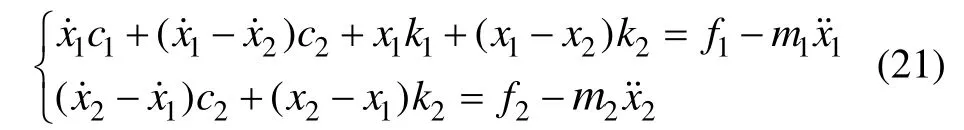
对每一个待求阻尼和刚度用前述方法展开，可以得到：

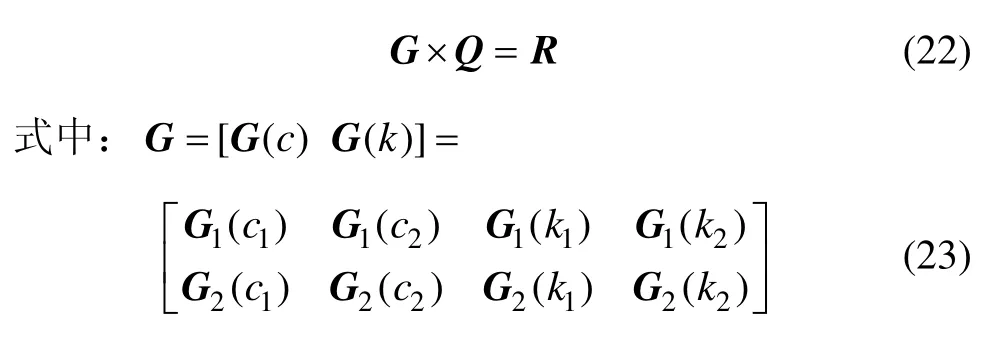
其中：展开系数G1(c2)的G1表示对于第一个方程；表示对应未知阻尼。与式(15)求法类似，只需根据的系数进行修改：

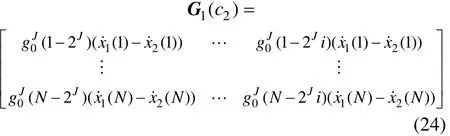
其他展开系数按相同方法可以求出。

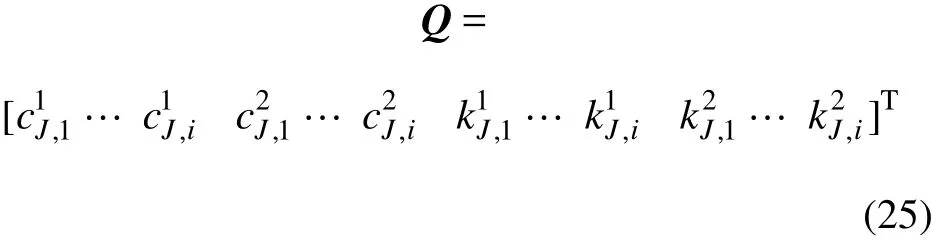
式中：上标1和2表示对应未知阻尼c1和c2以及未知刚度k1和k2。

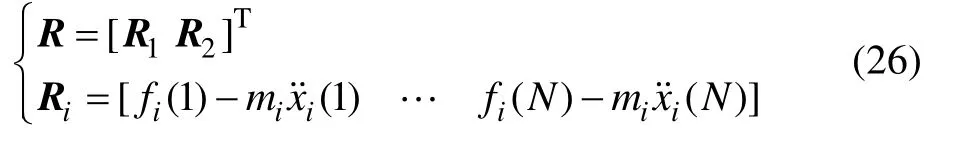
同样，对式(22)用最小二乘法可求出Q，从而识别出结构的时变阻尼和时变刚度。

当信号中存在噪音时，方程发生病态，直接用最小二乘法求解误差较大。这里采用Tikhonov正则化方法进行求解。

3 数值算例

采用如图3所示2层剪切框架结构模型做仿真算例，以验证本文方法的真确性和有效性。

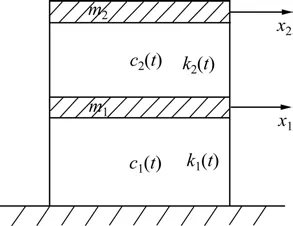
图3 2层剪切框架模型Fig.3 Two stories shearing frame model

模型质量保持不变，m1=m2=2.5 t。结构受到地震作用(取40 s El-Centro波作用)，用四阶龙格库塔法求结构的响应，采样频率为50 Hz。为模拟噪音影响，向求得的响应中添加高斯白噪声，考虑2种时变情况：刚度阻尼同时变化和只有刚度变化。

3.1 刚度和阻尼同时变化

考虑刚度K1突变，刚度K2线性变化，阻尼C1突变，阻尼C2线性变化，具体变化如下：

采用db3小波将时变参数展开，用提出的方法对刚度和阻尼进行识别，识别的刚度结果如图4和图5所示，识别的阻尼结果如图6和图7所示。

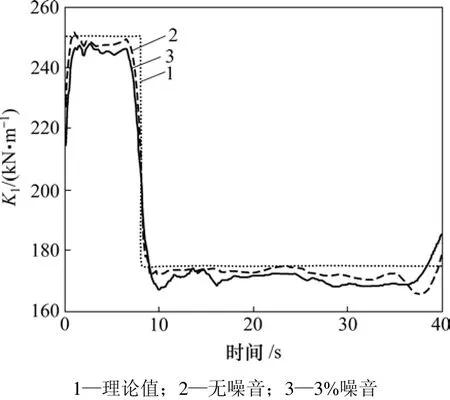
图4 刚度K1识别结果Fig.4 Identified results of stiffness K1

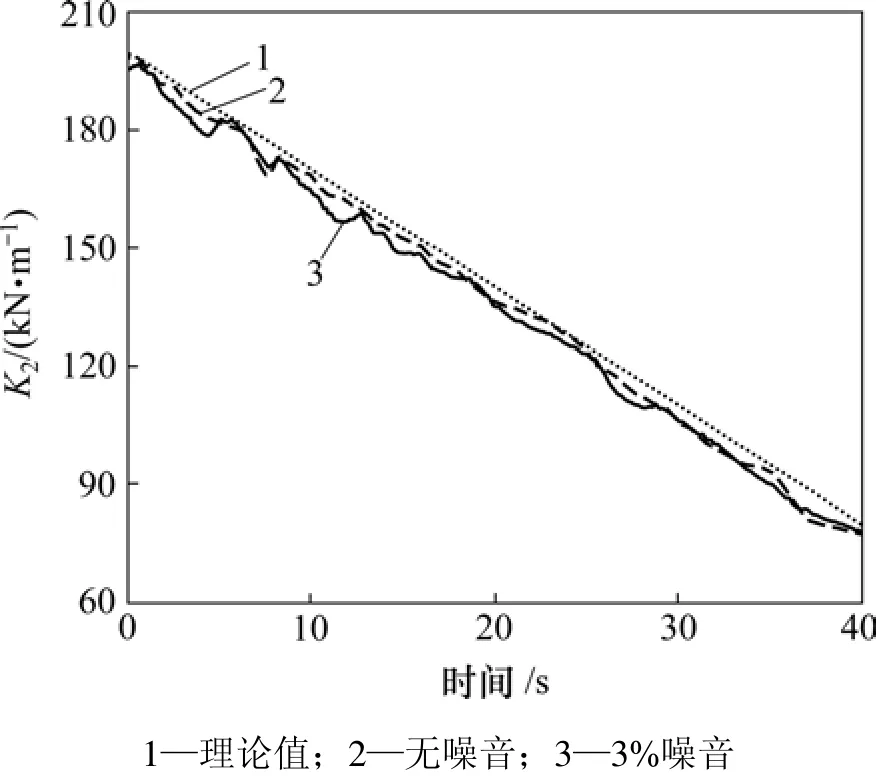
图5 刚度K2识别结果Fig.5 Identified results of stiffness K2

图6 阻尼C1识别结果Fig.6 Identified results of damping C1

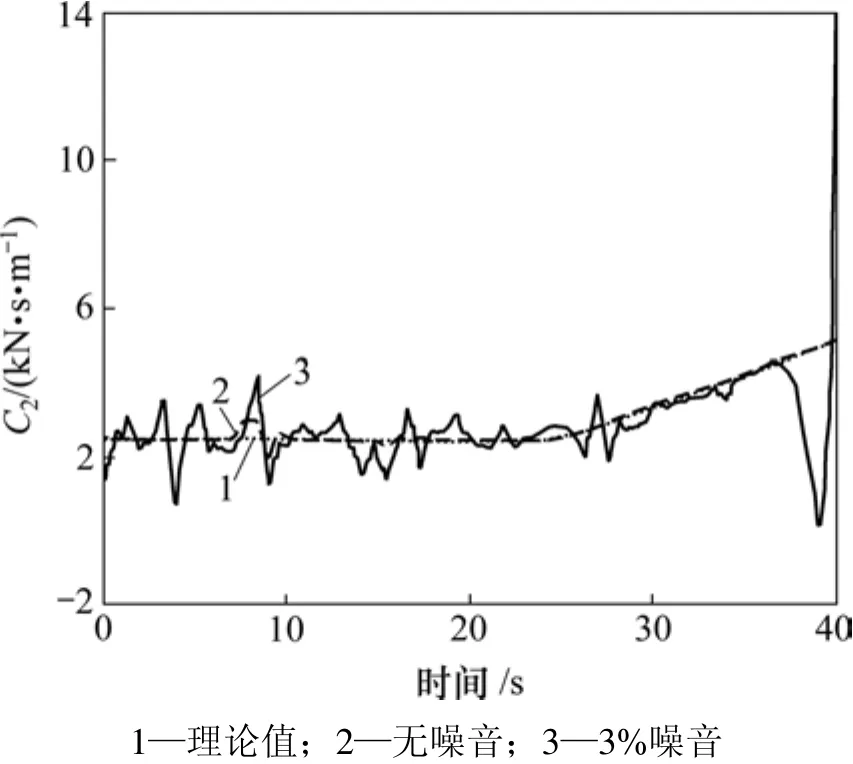
图7 阻尼C2识别结果Fig.7 Identified results of damping C2

由图4和图5可以看出：刚度的识别结果在无噪音时比较理想；存在噪音时，结果会受到一定影响，但仍能有效跟踪时变参数的变化。在刚度突变处，识别结果有一个过渡段，主要是由于方法对时变参数展开时只采用了低频概貌信号而忽略了高频细节信号，具有一定的近似，刚度突变处的高频成分被忽略，因而识别结果存在一定误差。另外，阻尼突变处的近似也会对整个识别结果产生一定影响。在信号的端部，由于小波变换端点效应的影响，识别结果也产生稍大偏离。时变阻尼的识别结果对噪音较敏感，但仍能看出其变化趋势。

3.2 刚度变化，阻尼不变

阻尼为C1=C2=1 kN·s/m，刚度K1二次曲线变化，刚度K2呈周期性变化，变化如下：

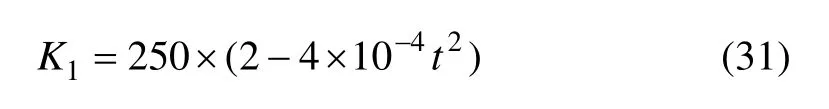
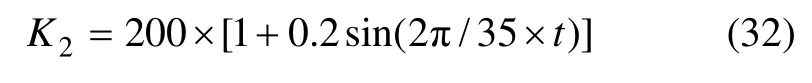
刚度的识别结果如图8和图9所示。由图8和图9可以看出：无噪音时，识别结果与理论值非常接近，只在端部由于端点效应的影响稍有偏差。主要是由于阻尼不变，刚度的变化也比较平滑，忽略高频细节信号产生的误差较小；当噪音加大到 5%时，刚度识别结果仍然较好，因而该方法识别刚度抗噪性较好。

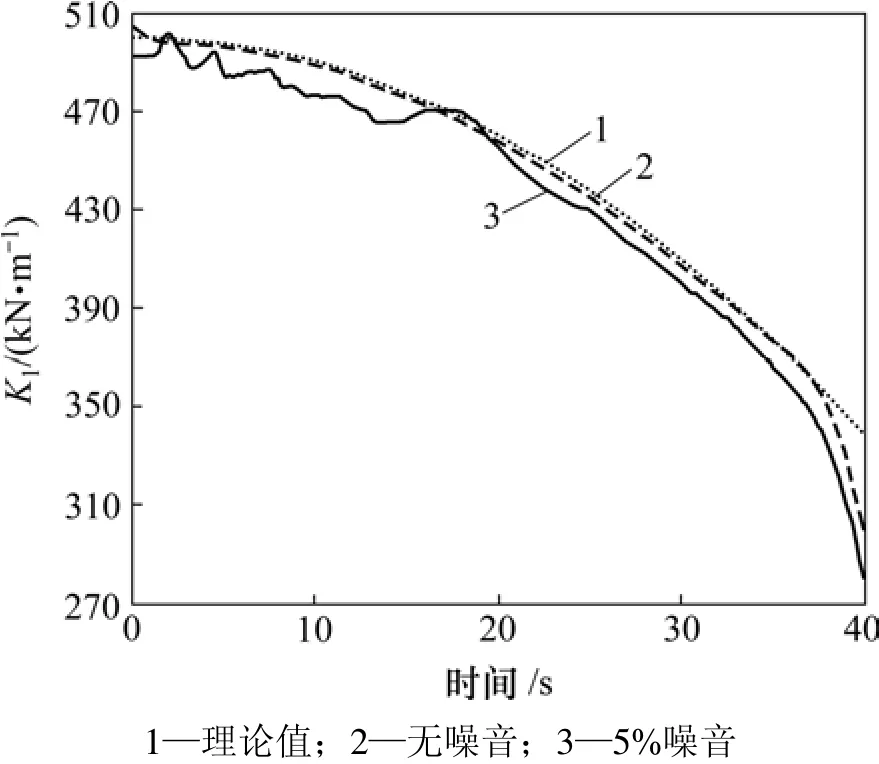
图8 刚度K1识别结果Fig.8 Identified results of stiffness K1

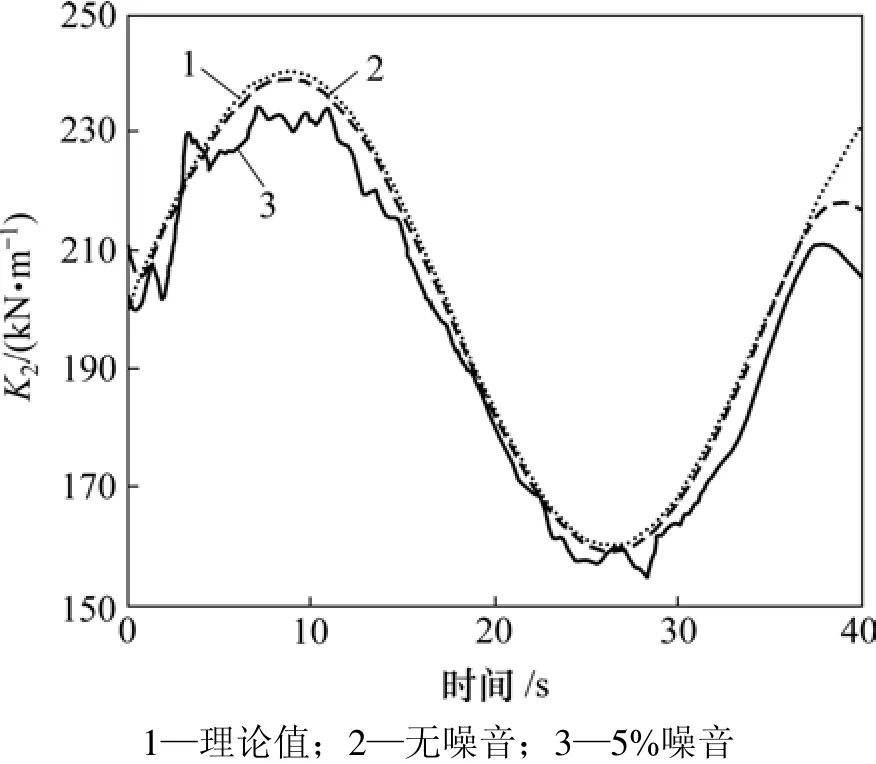
图9 刚度K2识别结果Fig.9 Identified results of stiffness K2

4 结论

(1)利用离散小波变换将时变结构的时变物理参数在多尺度上展开为概貌信号和细节信号，将时变结构识别问题转化为时不变结构识别问题，由最小二乘法识别出结构的时变物理参数。该方法可以有效识别结构的时变刚度，具有较好的抗噪性。

(2)由于将时变参数在多尺度上展开时，忽略小波分解的高频信号，由低频概貌信号估计时变参数，方法具有一定近似，因此，当刚度呈线性及周期变化时，识别结果比刚度突变时的好。

(3)同时识别刚度和阻尼时，由于阻尼比刚度小得多(本文中小 2个数量级)，识别时计算的相对误差要比刚度的相对误差大得多，因此，阻尼识别结果对噪音较敏感，误差较差，还需进一步研究、改进。

[1]续秀忠, 张志谊, 华宏星, 等. 结构时变模态参数辨识的时频分析方法[J]. 上海交通大学学报, 2003, 37(2): 122-126.XU Xiu-zhong, ZHANG Zhi-yi, HUA Hong-xing, et al.Time-varying modal parameter identification with time-frequency analysis methods[J]. Journal of Shanghai Jiaotong University, 2003, 37(2): 122-126.

[2]续秀忠, 张志谊, 华宏星, 等. 应用时变参数建模方法辨识时变模态参数[J]. 航空学报, 2003, 24(3): 230-233.XU Xiu-zhong, ZHANG Zhi-yi, HUA Hong-xing, et al.Identification of time-variant modal parameters by a time-varying parametric approach[J]. Acta Aeronautica et Astronautica Sinica, 2003, 24(3): 230-233.

[3]Liu K. Identification of linear time-varying systems[J]. Journal of Sound and Vibration, 1997, 206(4): 487-500.

[4]Liu K, Deng L. Experimental verification of an algorithm for identification of linear time-varying systems[J]. Journal of Sound and Vibration, 2004, 279(3): 1170-1180.

[5]庞世伟, 于开平, 邹经湘. 识别时变结构模态参数的改进子空间方法[J]. 应用力学学报, 2005, 2(2): 184-188.PANG Shi-wei, YU Kai-ping, ZOU Jing-xiang. Improved subspace method with application in linear time-varying structural modal parameter identification[J]. Chinese Journal of Applied Mechanics, 2005, 2(2): 184-188.

[6]吴日强, 于开平, 邹经湘. 改进的子空间方法及其在时变结构参数辨识中的应用[J]. 工程力学, 2002, 19(4): 67-70.WU Ri-qiang, YU Kai-ping, ZOU Jing-xiang. An improved subspace method and its application to parameter identification of time-varying structures[J]. Engineering Mechanics, 2002,19(4): 67-70.

[7]Hou Z K, Hera A, Shinde A. Wavelet-based structural health monitoring of earthquake excited structures[J]. Computer-Aided Civil and Infrastructure Engineering, 2006, 21(4): 268-279.

[8]Hera A, Shinde A, HOU Zhi-kun. Issues in tracking instantaneous modal parameters for structural health monitoring using wavelet approach[C]//Proceedings of the 23rd International Modal Analysis Conference (IMAC XXIII).Orlando, 2005: 338-347.

[9]Tsatsanis M K, Giannakis G B. Time-varying system identification and Model Validation using wavelets[J].Transactions on Signal Processing, 1993, 41(12): 3512-3523.

[10]Shi Z Y, Law S S. Identification of linear time-varying dynamical systems using Hilbert transform and empirical mode decomposition method[J]. Journal of Applied Mechanics, 2007,74(2): 223-230.

[11]Ghanem R, Romeo F. A wavelet-based approach for the identification of linear time-varying dynamical systems[J].Journal of Sound and Vibration, 2000, 234(4): 555-576.

[12]Cooper J E, Worden K. On-line physical parameter estimation with adaptive forgetting factors[J]. Mechanical Systems and Signal Processing, 2000, 14(5): 705-730.

[13]Yang J N, LIN Si-lian. On-line identification of non-linear hysteretic structures using an adaptive tracking technique[J].Non-linear Mechanics, 2004, 39(9): 1481-1491.

[14]李会娜, 史治宇. 基于自由响应数据的时变系统物理参数识别[J]. 振动工程学报, 2007, 20(4): 348-351.LI Hui-na, SHI Zhi-yu. Physical parameter identification of time-varying system based on free response data[J]. Journal of Vibration Engineering, 2007, 20(4): 348-351.

[15]任宜春, 易伟建, 谢献忠. 地震作用下结构时变物理参数识别[J]. 地震工程与工程振动, 2007, 27(4): 98-102.REN Yi-chun, YI Wei-jian, XIE Xian-zhong. Identification of time-variant physical parameters of structure under earthquake loading[J]. Journal of Earthquake Engineering and Engineering Vibration, 2007, 27(4): 98-102.

[16]杨福生. 小波变换的工程分析与应用[M]. 北京: 科学出版社,2000.YANG Fu-sheng. Engineering analysis and application[M].Beijing: Science Press, 2000.