一种多天线接收的全响应CPM信号解调方法

邵怀宗 吴 迪 周 莹

(电子科技大学通信与信息工程学院,四川成都610054)

1.引 言

自AULIN T.[1-2]于1981年发表连续相位调制(CPM)的论文以来,由于其是一种频谱效率和功率效率很高的恒包络传输技术,引起了国内外学者的广泛关注,并得到广泛的应用,如深空无线通信。但是,CPM调制是一种有记忆的调制方式,且传输符号的频率间隔小,通常小于系统传输的符号率。因此接收端通常需要采用匹配滤波器组加Viterbi检测器的方案[3-4],但这种结构处理起来非常复杂。且由于CPM信号本身的相位连续特性,符号与符号之间没有明显的幅度跃变,因此符号同步与载波同步非常复杂,即使发送训练序列的情况下,符号和载波同步也非常复杂。而基于常规的FSK调制的非相干检测技术,如包络检波、鉴频通常无法使用或者性能很差。目前基于CPM信号的接收的研究主要集中在如何对匹配滤波器和Viterbi结合的检测结构进行简化设计。通常导频序列的发送会导致系统的频谱效率的降低,在实际工程应用中有的特殊场合是得不到训练序列的,因而需要对系统进行盲处理[5]。此时,符号的盲同步是信息恢复的基础,然而即使在信噪比比较高的情况,盲同步算法的复杂度也非常高。文献[6]提出了非相干序列解调的方法,算法的稳定性较差,且仅适用于具有导频的情况。

针对CPM信号解调的困难,本文结合多天线分集接收技术,提出了一种新的基于短时Fourier变换加插值的非相干处理的方法来解决全响应CPM信号的解调问题。由于该方法是一种非相干方法,其同步可以在恢复的基带信号上进行,从而大大简化了整个解调过程。该算法不仅适用于具有导频的系统,也适用于没有导频的特殊情况;而且还适应不同的调制指数和不同的升余弦滚降因子的相位成型波形。在第2部分中给出了提出算法的基本原理,第3部分给出算法的仿真和分析结果,最后给出总结和相应的结论。

2.算法的基本原理

发送CPM信号的一般模型为

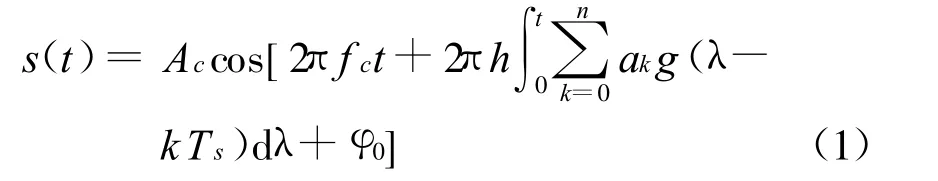
式中：n(t)为加性白噪声信号;h是调制指数。携带信息的基带信号为

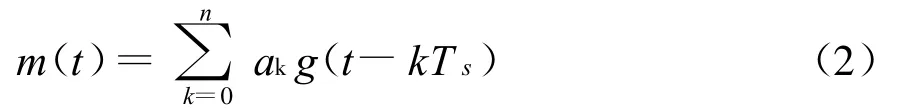
用该信号去改变载波信号的频率来将信息加载到相应的带通信号上去。对于M进制系统,∈[±1,±3,…,±(M-1)],如M=2的二进制系统ak∈[-1,+1],M=4的四进制系统∈[-3,-1,+1,+3],Ts是符号周期是载波频率,为初始相位,不失一般性,设 φ0=0。g(t)是持续时间 LTs的脉冲波形,称为频率成型脉冲,且满足=0.5,L为大于等于1的正整数,当L=1时,为全响应的CPM,否则称为部分响应系统。

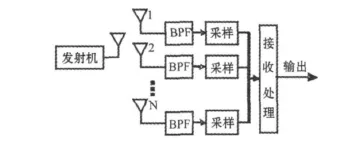
图1 基于多天线分集接收的CPM系统

对CPM信号进行多天线分级接收时,其系统的原理框图如图1所示。设有 N个天线同时对信号进行接收,各个支路分别对接收信号进行采样,然后送入接收处理单元。在接收处理单元中,首先对接收信号进行短时Fourier变换,然后求取能量最大的谱线和次大谱线,接下来利用这两个谱线和窗函数的特性进行插值处理来获取每次Fourier变换后谱线包络最大处对应的频率值,并将各路获得的频率值进行合并,可以选取等增益合并,也可以选择最大比合并,得到m(t)的估计最后利用(t),并在基带上进行同步处理,在最佳采样时刻获得用于判决的采样值。这里需要注意的是,由于调制指数的不同,估计出的与调制信号m(t)相比,其幅度有些差异。由于符号定时同步在基带信号上进行,从而算法得到大大的简化。

第i个天线上的接收信号可以表示为

式中：由于不同的路径具有不同的衰减,用衰减因子ai(t)表示,ni(t)是该路上的均值为0方差为的高斯噪声。并假设各路上的噪声统计特性相同,但彼此独立。

由上面的调制信号可知,在全响应系统中,每个符号内的信号不一定是单频的正弦信号。因此,对于一般的情况下使用鉴频的方法来处理,会产生较大的偏差。为了解决这一问题,这里使用短时Fourier变换,并计算每次短时Fourier变换后对应的谱线的最大包络值处所对应的频率。其方法是,在获得短时Fourier变换后,利用能量最大和次大的两根谱线通过插值来获得谱线的最大包络。其插值算法的基本原理如图2所示。假设某单频信号经过

图2 窗函数的频谱函数

窗函数序列{w(n),n=0,1,…,N-1}截断后进行Fourier变换,其频谱为W(n),频谱中能量最大的两根谱线出现在Fourier变换的n和n+1的两根谱线上,且这两根谱线是其主瓣内的两个谱线。因此,其频谱的最大值应在这两个谱线之间的x处,要求出谱线的最大包络值对应的频率,可以使用如下的插值方法。由于

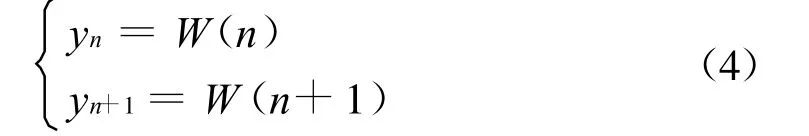
由于对于某一确定的窗函数,其幅度谱是已知的,可以定义一个新函数为

此函数是主瓣最大两个相邻谱峰的幅度的比值,是关于n的函数。其反函数为

根据窗函数的频谱的对称特性,可得频率校正因子为

校正后的频率为

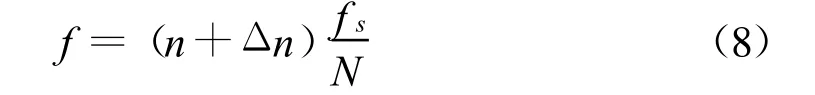
3.算法的仿真与分析

为了验证上述算法,下面将进行2、4和8进制的连续相位调制信号的解调进行仿真验证。设在每帧数据前面加上了20个符号的同步头,用于各路的同步处理。如果没有同步头,可以通过相关处理,也可使各个天线之间精确同步。且使用的频率成型函数为

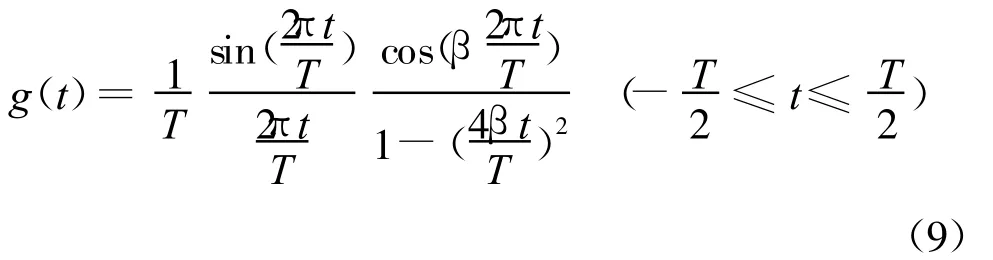
式中：β是滚降因子。

图3给出了Eb/N0=10 dB的情况下,4天线分集接收后2、4和8进制信号进行解调合并后得到的基带信号与发射端发送的基带信号的对比。其中,图3(a)、(c)和(e)分别是发射机对应的2、4和8进制全响应CPM 信号的基带调制信号,而图3(b)、(d)和(f)分别是它们通过接收处理后解调出来的基带信号,天线之间的信号组合采用最大比合并。从该图可清楚地看出,使用本文提出的非相干解调后可较好地恢复出基带信号,虽然波形整体上相差一个一个常数因子,但只要选择合适的判决门限则可以有效地恢复出传输的信息。

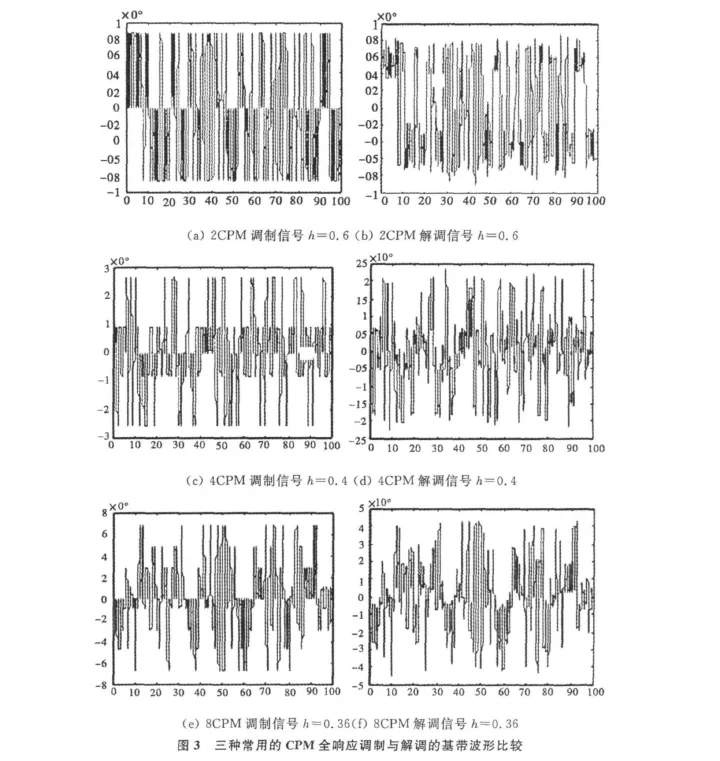
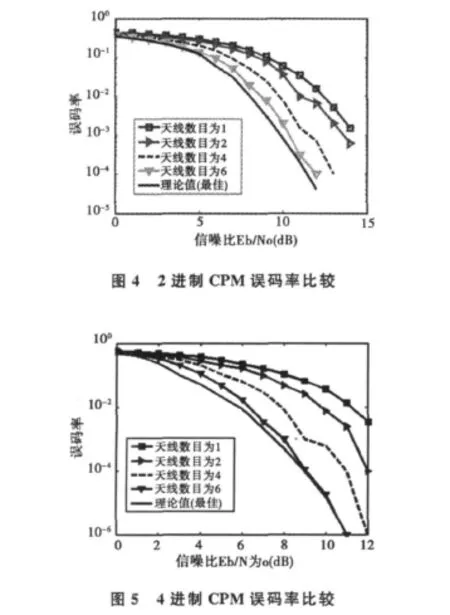
图4给出了使用该算法进行非相干解调后的二进制CPM信号误码率与最佳检测的误码率的分析比较。图5给出了4进制CPM使用天线分集接收后的误码率随天线数目增多而变化的情况。从图4和图5可以看出,该算法可以进行有效的解调,即使调制指数较小,即调频的频率间隔小于符号率的情况下,同样可以通过该方法较准确地鉴别信号的频率;如果接收机使用单个天线时,由于受到噪声和信道衰落的影响,鉴频的精度有限,但是随着天线数目的增多,分集增益的增大,系统性能逐渐接近系统最佳接收情况下的性能。

4.结 论

针对连续相位全响应系统,提出了一种基于短时Fourier变换加插值的方法来获得相应的时隙内信号的最大频率估计,即鉴频来获得信号的瞬时频率,并通过减去其均值来获得相应的频率调制基带信号的估计。为了有效抑制噪声和信道衰落带来的信噪比不稳定而引起该算法的鉴频误差,在接收机中引入多天线接收,利用分集增益来提高接收机的性能。仿真结果表明,该算法有效。与相干解调相比,虽然采用天线分集接收增加了接收机的硬件复杂度,但该非相干解调方法有效避免了相干解调时需要的复杂同步处理,从而大大简化了接收机的处理复杂度。

[1]AULIN T,SUNDBERG C.Continuous phase modulation-partl：Full response signaling[J].IEEE Transactions on Communications,1981,29(3)：196-209.

[2]TORAULIN,RYDBEE N,SUNDBERG W.Continuous phase modulation-partiI：part response signaling[J].IEEE Transactions on Communications,1981,29(3)：210-225.

[3]TANG Wei yi,SHWEDYK E.M L estimation of symbol timing and carrier phase for CPM in walsh signal space[C]//IEEE T ransactions on Communications,2001,49(6)：969-974.

[4]ZHAO Q,ST UBER G L.Robust time and phase synchronization for continuous phase modulation[J].IEEE Transactions on Communications,2006,54(10)：1857-1869.

[5]邵怀宗,吴 颖.一种新的适用于高阶QAM系统的均衡算法[J].电波科学学报,2009,24(5)：961-965.SHAO Huaizong,WU Yin.A novel equalization algorithm for high-order QAM system[J].Chineses Journal of Radio Science,2009,24(5)：961-965.(in Chinese)

[6]COLAVOLPE G,RAHELI R.Noncoherent Sequence Detection of Continuous phase modulations[J].IEEE Transactions on Communications,1999,47(9)：1303-1307.

[7]方继承.CPM低复杂度解调与同步算法的研究[D].博士论文,国防科学技术大学,2007.FANG Ji cheng.Research on Low-complexity Demodulation and Synchronization Algorithms of CPM,Dissertation School ofNational University of Defense Technology,2007.