转子-轴承系统局部碰摩故障机理研究

张 楠，刘占生，姜兴谓

(1.哈尔滨工业大学，哈尔滨 150001；2.北京航天动力研究所，北京 100076)

在旋转机械中,碰摩是一种常见故障现象,由于受转子和定子间隙的限制,以及不可避免存在的转子质心偏移,两者之间经常发生碰撞,导致机械结构的磨损,甚至引起严重损害。由于碰摩改变了转子系统的力平衡和动刚度,使旋转机械的正常工作条件受到破坏。动静件的碰摩通常由其他故障所引起,比如转子不平衡、转子及静止部件的弯曲、不对中、热膨胀造成的间隙不足等。碰摩使转子及静子受到切向摩擦力和冲击力作用。在一定条件下,这种突加激励可使转子产生反进动,严重时会使振动不断加剧,导致失稳,使旋转机械无法正常运转。转子系统碰摩问题的研究一直是转子动力学研究的重要课题,许多学者对转、静子碰摩问题进行了广泛的研究[1-7]。下文以某高速泵转子系统为例进行局部碰摩故障仿真研究，分析了偏心距、转速、半径间隙、摩擦因数及静子径向刚度等因素对系统振动特性的影响，进一步揭示了碰摩转子系统的运动状态与特点,为工程实际中复杂转子系统的优化设计、故障诊断及振动控制等提供了理论依据。

1 高速碰摩转子系统非线性动力学模型

1.1 转子轴承系统的建模

图1为某高速泵轴承支承下的碰摩转子动力学模型。不考虑摩擦产生的热效应，转子与静子的径向局部碰摩力模型如图2所示。其中，Pr为径向碰摩力，Pt为切向摩擦力，φ为接触点的向径与x轴的夹角，Ω为转子转动角速度，e为转子偏心距。转子与静子间的径向碰摩力采用线性当量弹簧模型，切向摩擦力采用库仑摩擦力模型，则当r>δ时，碰摩力、摩擦力分别为:

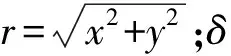
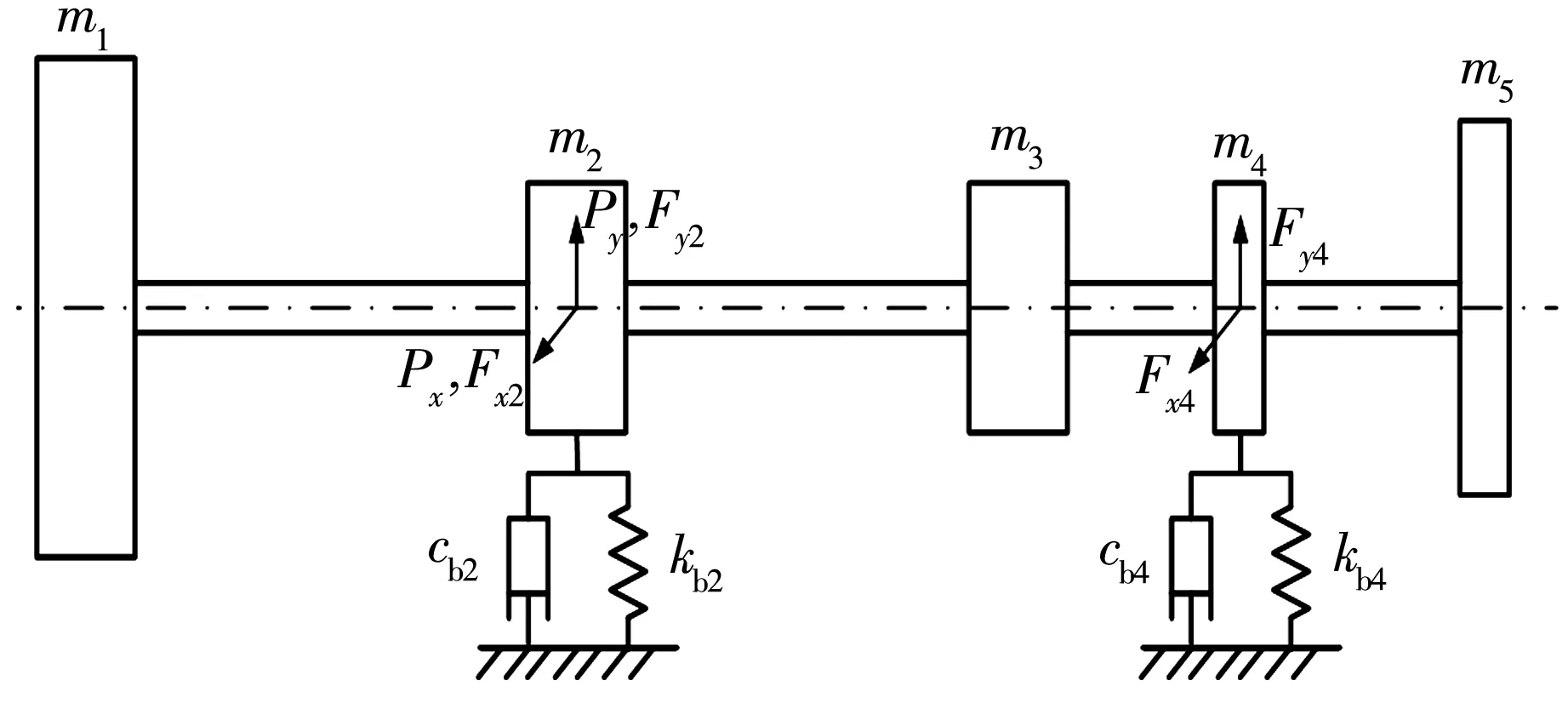
图1 转子轴承系统动力学模型

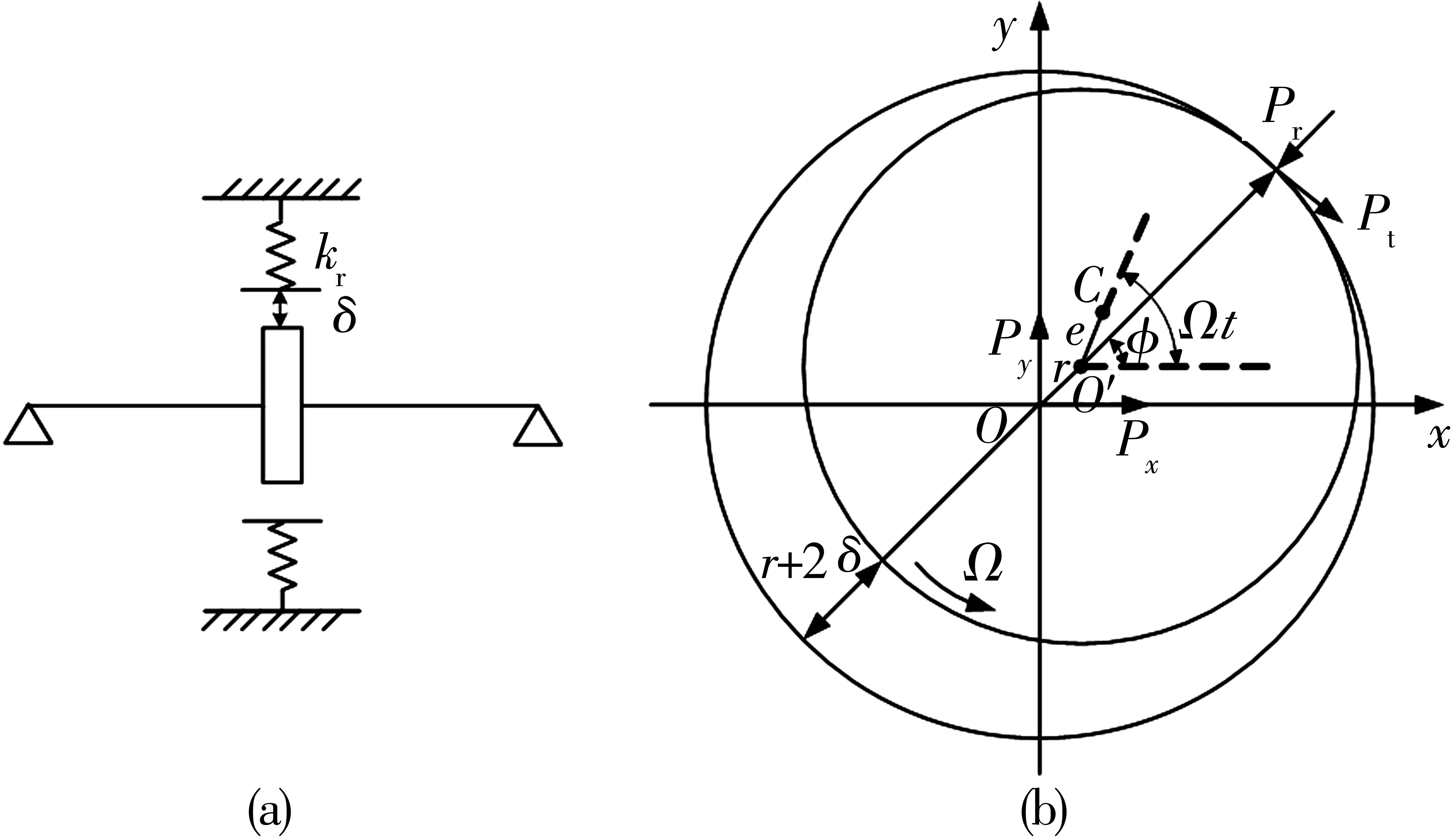
图2 转子与静子的径向碰摩力模型

碰摩力为:

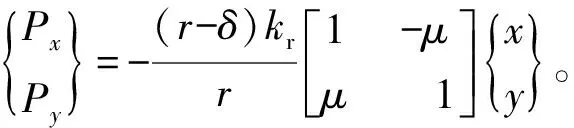
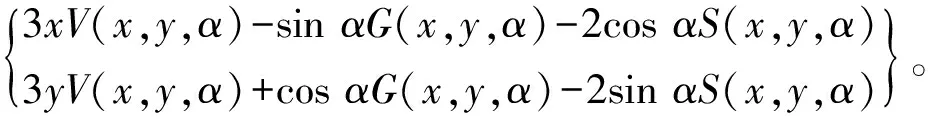
式中：τ为Sommerfeld修正数，τ=ηΩRL(R/c)2(L/2R)2；η为润滑油黏度；R为轴颈半径；c为轴颈与轴承的半径间隙；L为轴承有效长度；α为油膜的起始动态边界角，由转子运动中轴颈中心的位置来确定。

图1的5个集中质量转子系统中，第1,5圆盘为等效悬臂圆盘；第3圆盘为转子支承中部等效圆盘(包括齿轮)；第2，4圆盘为滑动轴承支承处的等效圆盘。圆盘2，4处为不同长度和直径的滑动轴承，这两处圆盘受到非线性油膜力的作用，在圆盘2处施加碰摩力。根据Newton第二定律可建立5个质量转子系统的考虑自身重力、不平衡激励、非线性碰摩力和油膜力的运动方程为：

cos (Ωt+φ1)，

sin (Ωt+φ1)-m1g；

Fx2+Px，

过度娇宠。美国家庭心理学家约翰·罗斯蒙德认为，家长的关爱是幼儿成长的维生素，缺它不可，过多无益。像有些孩子手里拿着鸡蛋，但不知道怎样吃；鞋带松了，却不知道怎样系等。这些都是家长平时过于娇宠的结果，阻碍了幼儿自主意识确立和自主能力提高。

Fy2+Py-m2g；

Fx4，

Fy4-m4g；

sin (Ωt+φ5)-m5g。

式中：kbi，cbi为滑动轴承油膜刚度和阻尼系数，i=2,4；ki，ci为轴段弯曲刚度和转子内阻尼系数，i=1,2,3,4；P为碰摩力；F为油膜力；Φi为圆盘质量偏心初相位，(i=1,2,3,4,5)。

1.2 滑动轴承油膜刚度和阻尼系数的确定

为了简化处理，将滑动轴承视为各向同性，不考虑交叉项。对油膜刚度和阻尼系数的处理，取工作转速下左、右轴承x方向的刚度、阻尼值作为结点2,4处x,y方向的油膜刚度和阻尼值，即取

kb2=1.623 6×108N/m，cb2=1.914 9×105Ns/m，

kb4=2.523 3×108N/m,cb4=1.673 6×105Ns/m。

1.3 系统仿真参数的确定

将图1中5处的集中质量视为不计厚度的刚性薄圆盘。本例选取的转子系统的初始参数如表1～表3所示。其他参数如润滑油黏度η为0.015 Pa·s；摩擦因数μ为0.10；转、静子半径间隙δ为35 μm；静子径向刚度kr为6.551 6×1010N/m；等效轴密度ρ为0.1 kg/m3。

表1 仿真初始输入参数

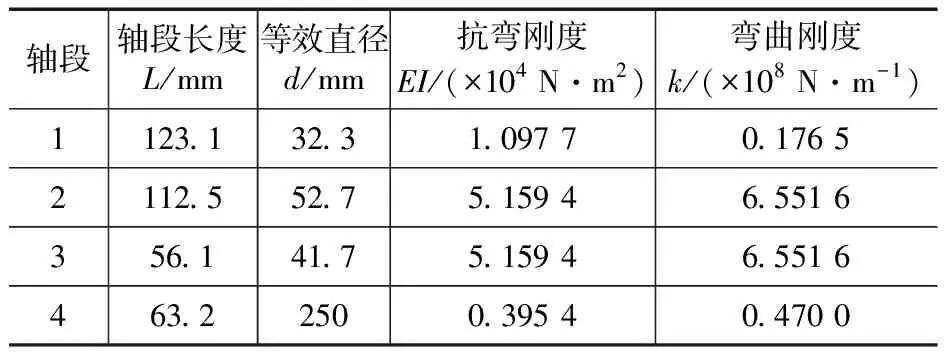
表2 仿真轴段输入参数

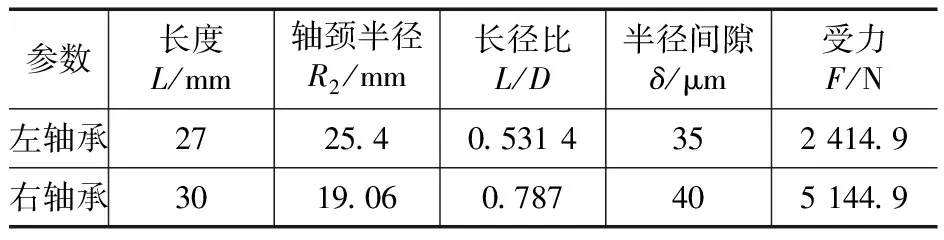
表3 仿真轴承输入参数

2 系统非线性动力学分析

正常运行的转子系统滑动轴承处很少发生碰摩，但由于转子不平衡、不对中，轴弯曲，轴颈半径间隙不均匀，动、静件热膨胀不一致及壳体变形等原因，可能导致轴颈处振幅显著增大或轴颈与轴承的径向间隙减小，从而引发轴颈与轴瓦的径向碰撞摩擦。影响转子系统稳定性和动力学特性的因素较多，主要有转速、偏心量、半径间隙、摩擦因数及静子径向刚度等。

数值仿真无量纲时间步长取π/200，Newmark方法的收敛偏差标准取10-6。仿真200个周期，舍弃非稳态数据，取后50个周期稳态数据进行分析。

因仿真在圆盘2(左滑动轴承)处发生碰摩，此处的振动特征最为显著，故主要研究圆盘2水平及垂直方向的振动特征。

2.1 偏心距的影响

将碰摩发生的条件设定为质量偏心距的增大进行仿真，研究碰摩故障发生的振动规律。

取圆盘2不同的偏心距值，保持其他参数不变，作系统随转速变化的振动特征图。偏心距e=2 mm时x2和y2的幅频曲线、分岔图和三维谱图如图3～图5所示。从图3可知，e=2 mm时，x2和y2的振幅接近滑动轴承半径间隙值为35 μm，尚未发生碰摩；振幅随转速的增大而增大，在19 600 r/min处有峰值，之后振幅下降，到22 400 r/min处又开始回升，后者对应于转子的弯曲振动一阶临界转速。从图4中得出系统未发生分岔，始终作周期运动。图5中三维谱图中只有基频分量，由于转子为轴对称结构，支承各向同性，圆盘重力的影响较弱，故水平和垂直方向的振动特性没有明显差别。

图3 x2和y2的幅频曲线

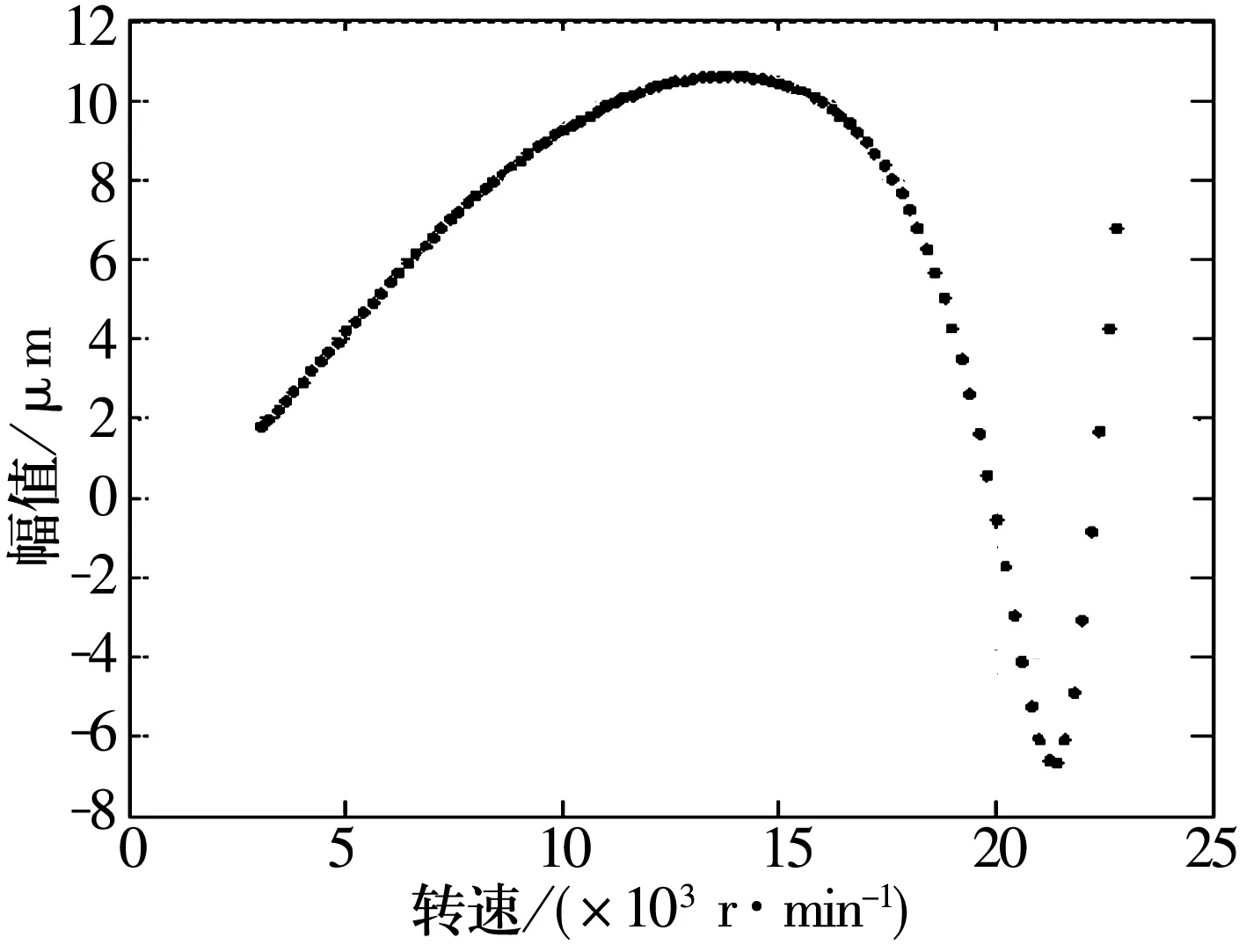
图4 x2分岔图

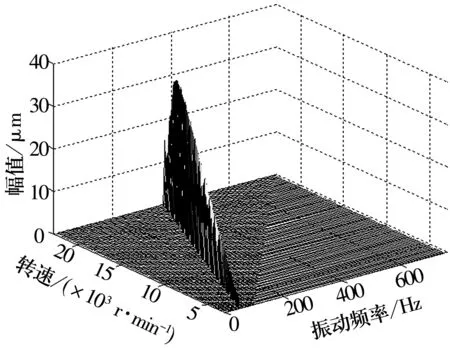
图5 x2三维谱图

偏心距e=5 mm时x2和y2的幅频曲线、分岔图和三维谱图如图6～图8所示。从图中可知，e=5 mm时，x2和y2振幅在10 000 r/min时达到滑动轴承的半径间隙值35 μm而发生碰摩，振幅保持稳定，在22 400 r/min处稍有变化；系统在10 000～11 000 r/min时发生分岔，即碰摩刚发生时系统运动不稳定，之后重新进入周期运动；三维谱图中谱峰在碰摩后保持稳定。

图6 x2和y2的幅频曲线

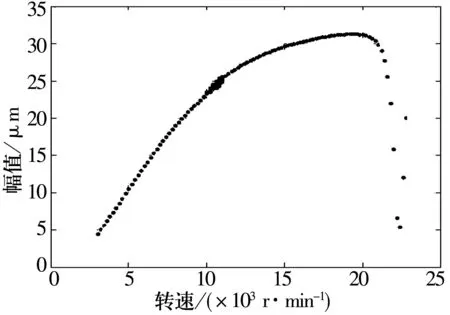
图7 x2分岔图

图8 x2三维谱图

偏心距e=10 mm时x2和y2的幅频曲线、分岔图和三维谱图如图9～图11所示。从图9可知，e=10 mm时，x2和y2的振幅在6 400 r/min时达到滑动轴承的半径间隙值而发生碰摩，振幅稳定中略有上升；系统在6 400～11 000 r/min时发生分岔，运动不稳定，之后重新进入周期运动。

图9 x2和y2的幅频曲线

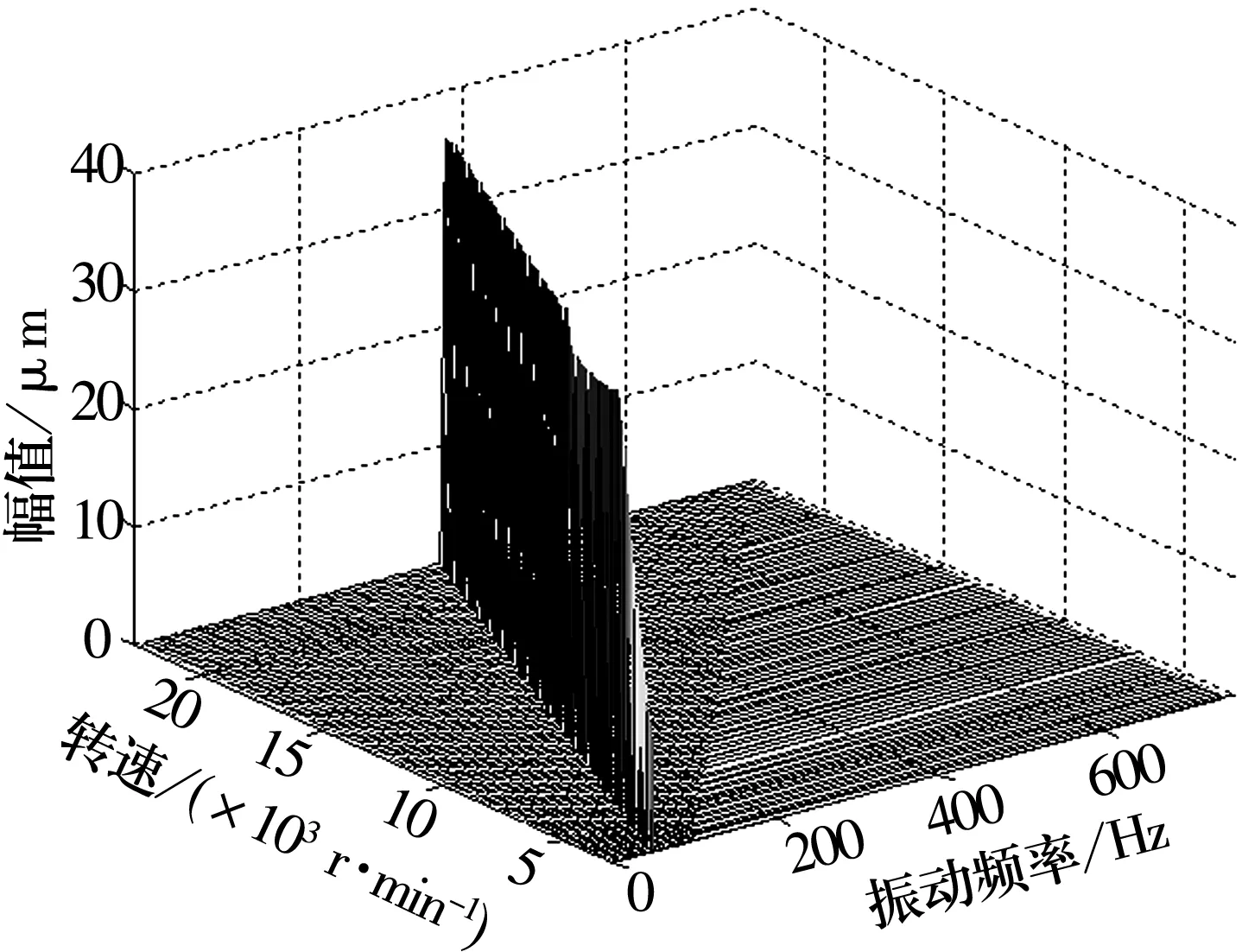
图11 x2三维谱图

2.2 半径间隙的影响

偏心距e=5 mm，转、静子半径间隙δ=20 μm时x2和y2的幅频曲线、分岔图和三维谱图如图12～图14所示。从图12可知，δ=20 μm时，x2和y2的振幅在7 000 r/min时达到半径间隙值而发生碰摩；系统在7 000～11 000 r/min时发生分岔，运动不稳定，之后重新进入周期运动。对比图6～图8可知，转、静子半径间隙的减小导致碰摩的发生和加剧，使得碰摩振幅减小、失稳转速下降、失稳转速范围拓宽。因此，转、静子半径间隙对碰摩系统振动特性的影响较为显著。

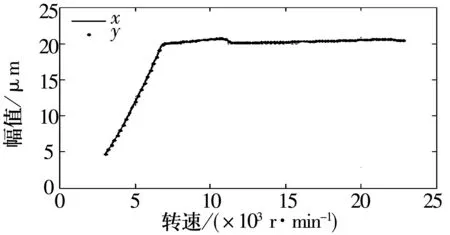
图12 x2和y2的幅频曲线

图13 x2分岔图

图14 x2三维谱图

2.3 摩擦因数的影响

偏心距e=5 mm，摩擦因数μ=0.2时x2和y2的幅频曲线、分岔图和三维谱图如图15～图17所示。从图15和16可知，μ=0.2时，x2和y2的振幅在10 000 r/min时达到滑动轴承的半径间隙值35 μm而发生碰摩，振幅保持稳定；系统在10 000～11 000 r/min时发生分岔，之后重新进入周期运动。对比图6～图8可知，摩擦因数的增大没有加剧碰摩，对系统振动特性的影响不大。

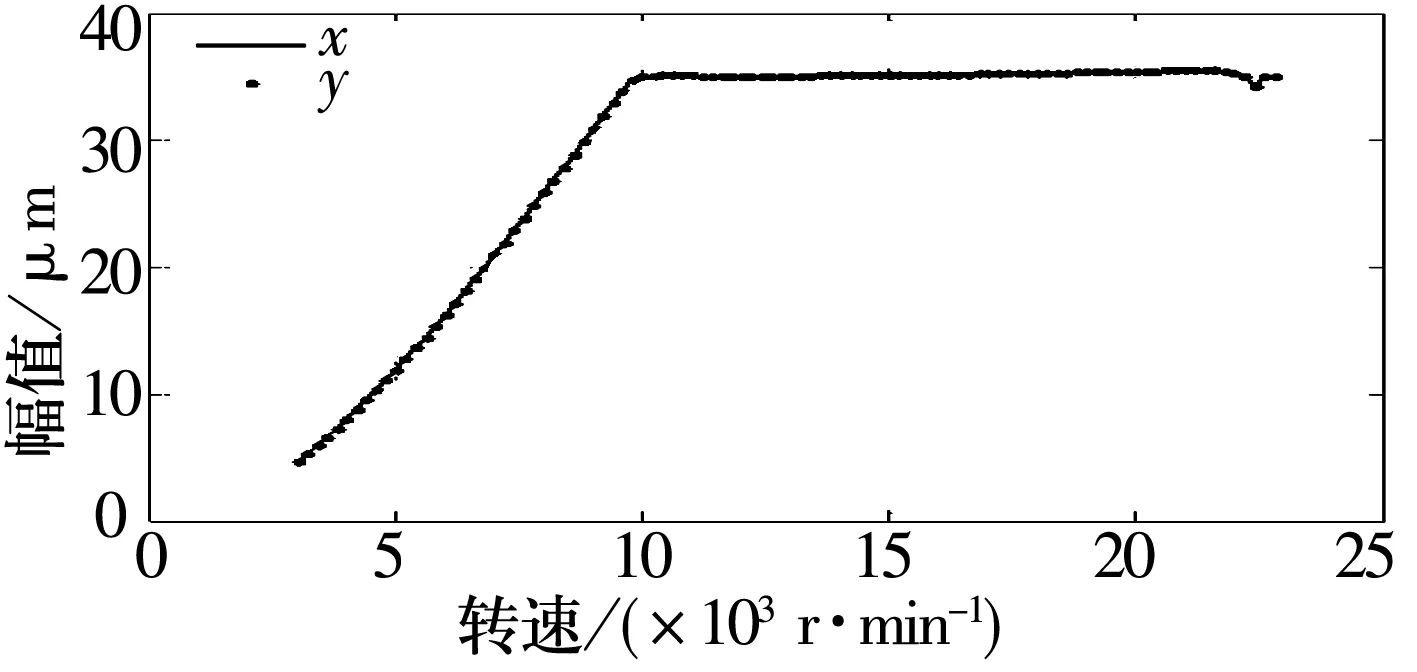
图15 x2和y2的幅频曲线

图16 x2分岔图

图17 x2三维谱图

2.4 静子径向刚度的影响

偏心距e=5 mm，静子径向刚度kr=1×108kN/m时x2和y2的幅频曲线、分岔图和三维谱图如图18～图20所示。从图中可知，kr=1×108kN/m时，x2和y2的振幅在10 000 r/min时达到动静间隙值而发生碰摩；系统在10 000～14 400 r/min时发生分岔，运动不稳定，之后重新进入周期运动。对比图6～图8，静子径向刚度的增大导致碰摩加剧，使得失稳转速范围拓宽。因此，在碰摩已经发生的情况下，静子径向刚度对碰摩系统振动特性的影响较为显著。

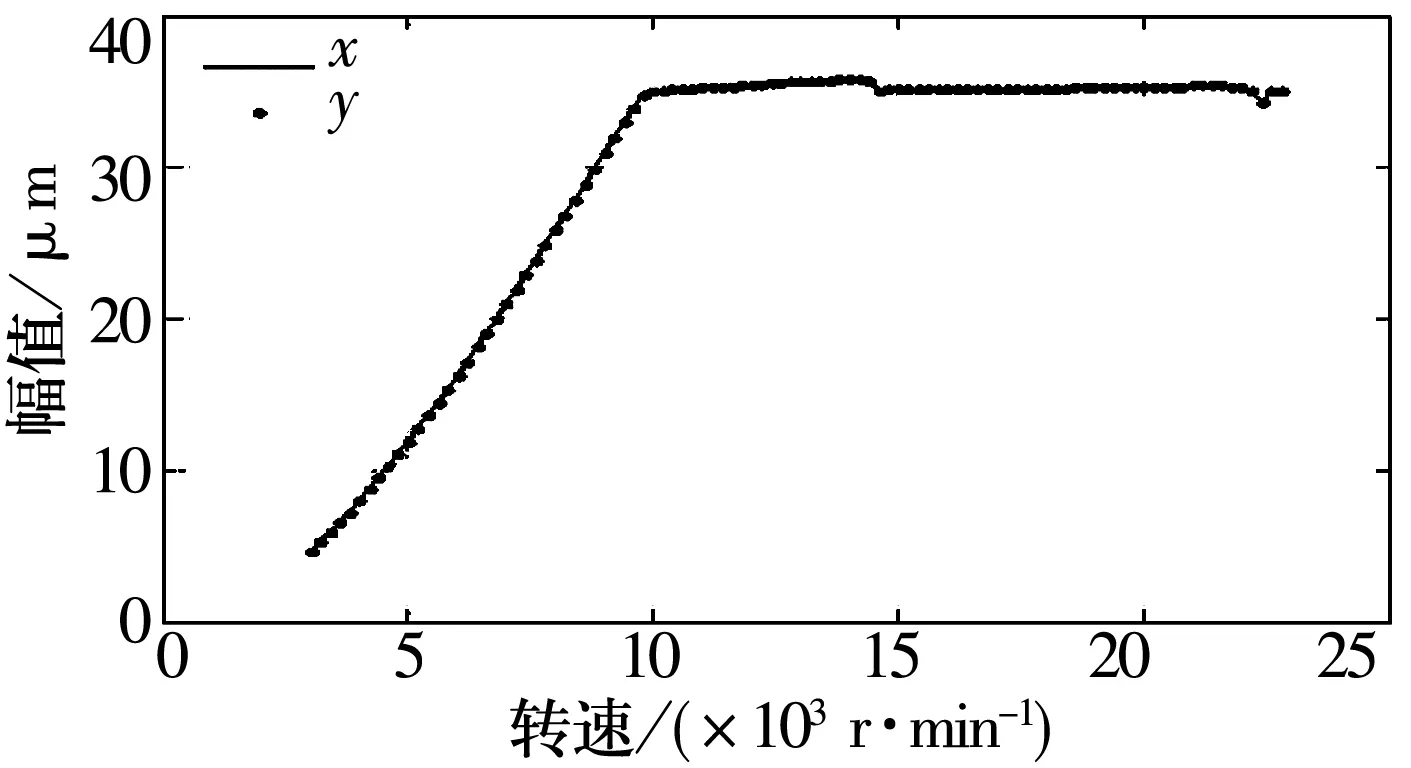
图18 x2和y2的幅频曲线

图19 x2分岔图

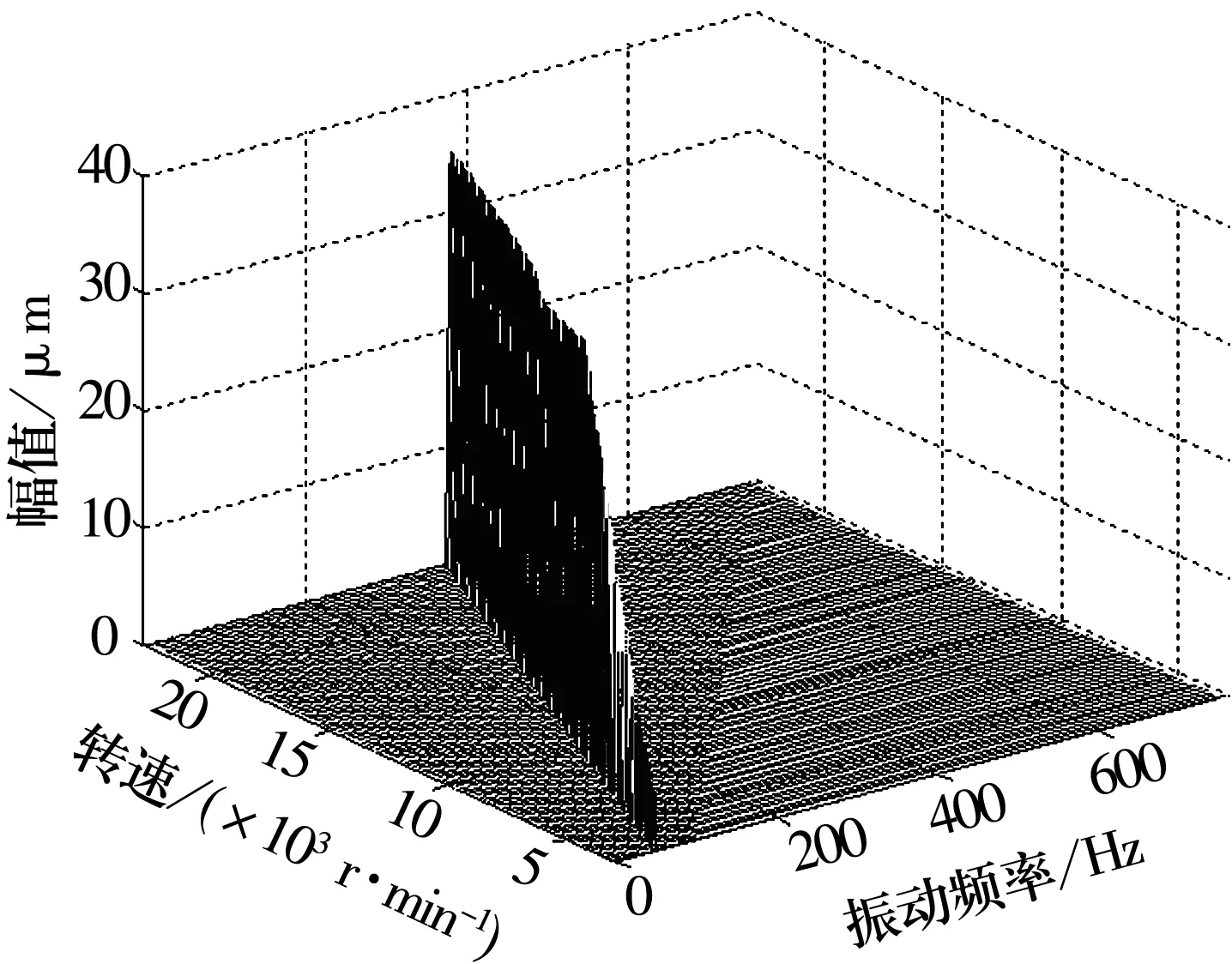
图20 x2三维谱图

3 结束语

建立了滑动轴承支承下的局部碰摩故障转子系统的动力学模型，在模型中考虑了碰摩故障的非线性，研究了不同参数对系统振动特性的影响。得出滑动轴承支承下的局部碰摩转子的振动特征频率以基频为主，正进动随着碰摩的加剧而出现倍频谐波分量，系统运动不稳定性增强。研究了偏心距、转速、半径间隙、摩擦因数和静子径向刚度等因素对碰摩系统振动特性的影响。

因此，在工程实际应用中要采取对不平衡量过大的转子进行严格的动平衡，确保动平衡精度；按设计要求调整好转子与静子的相对位置和间隙；调整转子对中度，改善壳体及基础的变形；选用刚性较好的轴，更换挠曲变形过大的转子；提高滑动轴承供油压力，以形成足以保证转子稳定运行的油膜，防止因油膜破裂而发生干摩擦等措施，以减少转子轴承系统发生碰摩故障。