物理问题解决中的良构图式初探

祝令健 陆建隆

(南京师范大学物理科学与技术学院,江苏南京 210046)

随着新课改的推进和深化,关于学生物理问题解决能力的培养和提高,因能综合体现对学生物理基础知识掌握、物理思维品质和物理科学方法的教学要求,已成为高中物理教学研究中的热点课题.近年来江苏省物理高考改革的发展也越来越重视与新课程思想的对接.图式作为一种积极的认知结构,对于解决知识丰富领域中的问题有很重要的作用[1].中学生物理图式的水平在很大程度上决定了其问题解决的顺利与否.本文在对图式这一心理学术语理解、研究的基础上,论述了图式和物理问题解决能力培养的关系,通过实例分析,对有利于提高学生解决物理问题能力的良构图式进行了初步的探讨.

1 图式

1.1 图式的概念

“图式”(schema)一词是心理学领域非常重要的概念,究其思想渊源,至少可以追溯到18世纪的德国哲学家康德.康德认为图式是指以一般的方式来构建概念的规则.值得注意的是,皮亚杰在其著作中广泛使用了图式这一概念,用它代表内化了的动作或一种心理结构.图式,连同顺应、同化和平衡等概念构成了皮亚杰发生认识论的概念基础,对心理学的研究产生了深远的影响.

目前,“图式”已经成为现代认知心理学的核心概念之一,它在很多关于问题解决和推理方面的文献中屡屡出现,但是对“图式”概念的理解尚无完全一致的看法.例如巴特莱特和布鲁尔(Bartlett&Brewer)认为,“图式是指为表征知识而建立的心理框架,包括对一些相关概念进行排列,使其成为一个有意义的组织体”[2],梅尔哈特和诺曼(Rmuelhart&Norman)曾将图式定义为“表征记忆中业已贮存的有关类概念(generic concept)的资料结构”[3].虽然上述关于图式的表述不同,但都认为图式是用以表征客观事物及其关系的某种知识或心理的结构、组织、框架,它是对一类事物的抽象概括,可以用来组织零散的刺激、信息和数据.因此,本文主要采用皮亚杰的观点,认为图式是指个体对某个对象的知觉、理解和思考的方式,是心理活动的框架或组织结构.

1.2 图式的分类

帕斯科尔◦里欧发展了皮亚杰的理论,进一步对图式进行了分类[4],帕斯科尔◦里欧把图式分为动作图式、形象图式、运算图式和执行图式.动作图式表示人对自己身体动态经验的感觉和理解.例如,做单摆实验时人的眼睛、手的协调动作图式.皮亚杰指出,儿童的动作图式是其将来高级图式的基础;形象图式是一些信息单位的表象,这样的表象是很多的.例如质点、单摆、电子、理想流体、刚体等;运算图式是把一个形象图式改变或转换成为另一个形象图式.例如,已知v(t)=3t2+5t-2,则加速度a(t)=?这种由速度得出加速度的计算,也需要运算图式.运算图式涉及数和逻辑规则的应用;在解决多种多样问题或任务时所形成的总策略属于执行图式.例如控制变量、物体受力情况分析等就属于执行图式.执行图式是支配动作图式、形象图式和运算图式的图式.

2 图式与中学物理问题的解决

2.1 图式在物理问题解决中的作用

图式是个体对某个范畴的知识的框架与概括,它不但在个体认知学习过程中发挥着重要的作用,而且在学习者进行物理问题解决时也发挥着重要的作用.

一方面,学习者的图式水平影响着对问题情境的知觉和对问题的理解.学习者在对物理问题情景的知觉中,通过感官吸纳大量信息,这些信息要获得进一步的注意和加工,必须加以过滤、分析和解释.为此,图式就要发挥作用,一个人的图式水平很大程度上反映了他对所给物理问题信息提取的能力.

要理解问题情境,就必须把它们纳入已有的图式才能获得一定的意义.要理解某问题提供的信息和本质,就必须依赖学习者已有的图式.因为知识是由若干相互联系的节点组织而成的语义网络,这种组织的主要方式就是图式,学习者从问题中捕捉到的一些信息,可以激活其中的一些信息可以激活其中的一些节点,进而激活相关图式,图式可以提供相关的知识和意义以补充问题情景缺失的或隐藏的信息,这常是问题解决者能迅速理解问题的本质所在.正如John B.Best指出的:“图式知识一旦被激活,就能引导问题解决者以特定的方式搜索问题空间、寻找问题的有关特征”[1].例如,一个没有学习过物理知识的小学生注意到天空中彩虹的有关信息时,他的头脑中存在关于该现象的图式,却没有关于该现象如何解释的图式,而对于一个物理学专业的大学生来说,他的头脑中不但有关于彩虹现象的图式,而且还有关于该现象解释的图式.

另一方面,图式水平也影响着对物理问题解决方法的获得.笔者们每个人都有成千上方的图式,在面临特定的物理问题情境时,只有正确选择所需图式,才能帮助我们选择恰当的策略来解决问题.图式选择是问题解决的重要部分,解题策略就以图式的选择为基础.对专家和新手的问题解决策略的研究表明,专家通常能熟练地运用手段——目的分析策略,利用问题中的信息向前求解;新手大多利用逆向推理策略,从所提问题逆向求解.新手的问题解决基本上是搜索驱动的,而专家是图式驱动的.可见图式与物理问题解决策略的选择及应用有着紧密的关系.

然而,图式的作用并不总是积极的,有时它可能会造成大量信息的丧失.由于图式发挥着过滤器的作用,大量信息就有可能被过滤掉.一般来说,忽略掉那些不能被同化的信息是有意义的,但是却可能破坏信息的全面获取,图式还常难以去除.一旦我们觉得世界以某种方式组织,我们就不愿丢掉这个观点,这就限制了图式的进一步获得.最后我们可能因使用了错误的图式而误导问题的解决.

图式不仅对问题解决有影响,反过来,问题解决也是获得图式的重要渠道.在解决新的问题时,人们会调用有关图式来指导问题的解决,在问题解决中,图式得以修正或概括化、专门化,这样就形成了新的图式.西蒙(Simon)就指出:“一旦人或计算机程序确定了这个问题所需要的图式,以及每个图式所需要的数据,然后就会把这些图式综合在一起变成一个新的图式——问题图式.在问题图式中说明了各个分图式的关系.”[5]因此,图式和问题解决是相互影响的.

2.2 物理问题解决中的图式类型

基于上述图式对物理问题解决的影响可知,学习者对物理问题解决的顺利与否在很大程度上决定于其相关图式的优劣.本文把有利于相关问题解决的图式称为良构图式;把不利于相关问题解决的图式称为劣构图式.那么相应地,我们可以把有利于物理问题解决的图式称为物理良构图式;把不利于物理问题解决的图式称为物理劣构图式.

当然,上面只是对良构图式和劣构图式的界定做了简单的说明,没有对其做具体、详实的概念性界定.主要原因是良构图式和劣构图式这种提法本身是放置于具体问题解决的背景下,它本身也具有一定的相对性.下面通过具体的实例对良构图式和劣构图式的特点和影响因素作一些阐述,这有助于大家对良构图式有比较清楚的认识和理解.

3 中学物理问题解决中的良构图式

作者为了研究图式的优劣对物理问题解决的影响和差别在2009年11月口语报告法把一道力学的物理题目对南京师范大学附属中学江宁分校高二年级的部分学生进行了测试.

题目.一个质量为 m的木箱放在水平面上,木箱与水平面间的动摩擦因数为μ.现有一个与水平方向成θ角斜向上的拉力F拉着木箱沿水平方向以速度v匀速前进.求:拉力F的大小?

为叙述方便起见,先做如下说明:

在介绍口语报告录音材料时,…表示短暂的停顿;……表示长时间的停顿;——表示语义转变;{……}表示听不清的模糊话语;[]表示笔者插入的内容.

这道题目正确求解的一般思路是:由题目的已知条件可知物体受力平衡,对物体受力分析:物体受重力G=mg,支持力 FN,摩擦力 f=μ FN和拉力F的作用.建立直角坐标系后,可把力F进行正交分解.由于物体受力平衡,所以∑Fx=0,∑Fy=0.然后列出等式进行求解,在此过程中,解题者相关图式外在的表现如图1所示.

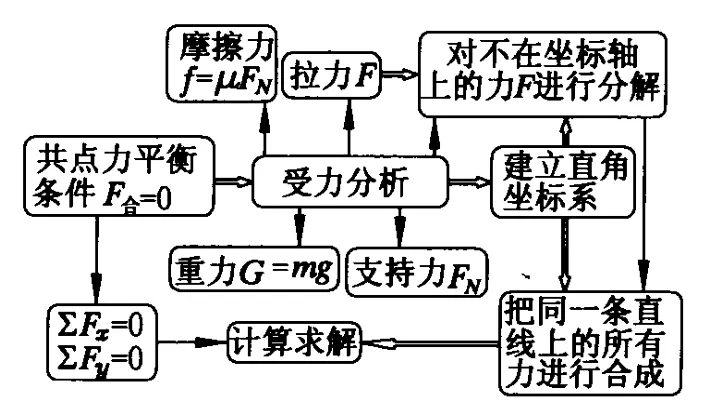
图1

下面,我们先看一位学生口语报告的录音材料:“题目—首先是…首先画图,木箱…在水平面上受力…拉力成θ角——斜向上,嗯,在水平方向上是以速度 v向前运动.F——可以首先求出水平拉力的F1,F1就等于个F…等于…说错了,错了……{……}[主试提醒他“说出来”]…F1就等于 F乘以cosθ…嗯……F1…[主试再次提醒他“把想到的说出来”]…这个题我感觉不会做,要么就是少条件……不做了”.

我们从以上口语报告材料可以看出,这位学生不光是相关的知识缺乏,而且所具有的一点相关知识还缺乏层次性,他似乎知道把拉力F分解为一个水平方向的力和一个竖直方向的力,并且水平方向力的大小他也说出来了,是“F乘以cosθ”,但他最终因为不知道求出这个 F1以后怎么用以及用在什么地方,故而没有把问题解决出来.很明显这位学生相关的图式既是知识点缺失的,也是层次不清的.

我们知道,图式是具有层次性的,而有些学习者,特别是某一领域的新手往往只是机械记忆了一些概念性的东西,没有完全搞清楚概念与概念之间的联系而致使其图式结构不清且缺乏层次性,这时的图式不但会导致其对题意理解产生偏差,并往往使其找不到合适的解题方法,从而影响其解题.另外,新手的知识往往是很局部的,相关知识的缺失或误用也会导致其知识点间不能很好地相互激活.所以,我们认为图式构造不良往往是影响良构图式构建的重要因素,而图式构造不良又主要表现在层次不清和知识点缺失上.

再看另一位学生的口语报告录音材料:“这个拉力是斜向上的,所以它可以分解,…匀速运动,它是没有加速度的,[……](主试提醒他“说出来”)呃,它的合力是零,那它水平方向的分力就等于它所受的摩擦力.μ mg就等于Fcosθ,…呃……F就等于μ mg比上cosθ[写成

这位学生由题目中“匀速运动”的条件激活了“合力是零”的知识,但是他在分析摩擦力时却遇到了问题.滑动摩擦力等于正压力乘以动摩擦因素,而这位学生习惯性地用木箱所受的重力来代替它与地面间的正压力.其解题过程中图式的外在表现如图2所示.

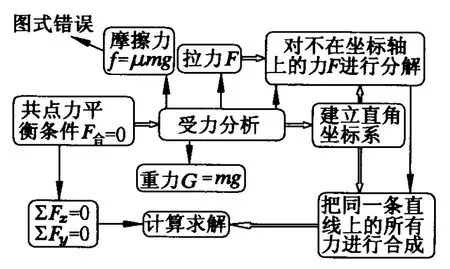
图2

测试中发现,同样的错误在其他学生中都存在,所以我们不能将这个问题归结为学生的马虎或者不仔细,应该说是学习者对相关知识点记忆或理解的错误.可以说图式的错误也是造成物理问题解决受阻的重要因素之一.这里的图式错误有两种原因所致:一种是知识点的错误,另一种是知识点间逻辑关系的错误.

学习者在接触到相关领域的知识后,如果没有经历一定的练习,可能会使图式内知识之间的网络连接并不很紧密,这样会导致在物理问题解决过程中,学习者并不能从一个知识点很流畅地激活另一个知识点.笔者在测试中发现,用同样的方法解决同一个问题时,有的学生很快就能由一个知识点激活到另一个知识点,而有些学生则要经历相当长时间的回忆及思考,况且后者还有一部分不能完成任务.所以,物理良构图式应该是知识点之间的连接比较强的图式,它能够容易地、由此及彼地进行相互激活.

如果学习者的图式结构涉及的局部性的知识,例如就是关于力与运动方面的,解决的也仅是部分的力学问题,这时我们称学习者的这种图式为局域性图式;如果学习者在解决问题时,能将各局域性图式配合着使用,能将2个或2个以上的局限性图式有机结合起来,具有清晰的层次性和知识点的相对完整性,我们就称学习者此时形成的这种图式为广域性图式.例如,学习者若能将力与运动的图式和能量部分的图式有机结合形成涉及力、运动和能量三者之间的认知图式,并能在解决相关问题时顺利地相互激活,而使问题得到解决,那么此时我们称这位学习者具有广域性图式.当然,从更高一层次的图式的角度看,上述“广域性图式”有时又会沦落为“局域性图式”,所以这里的广域性图式和局域性图式具有相对性的特点.一个良构图式往往在某知识体系范围应该是一个广域性的图式,因为这样才更有利于问题得到顺利的解决.Sabella曾在Maryland大学对此问题做过一些研究[6],表明具有相对广域性图式的学习者在解决物理问题时往往比较顺利,而只具有一些零碎的、相互间不能有机结合的局域性图式的学习者,在解决物理问题时往往会遇到一些困难,特别在解决一些能力立意较高、综合性较强的物理问题中往往因“只见树木,不见森林”而无法正确获得问题的解决.

一般来说,在物理问题的解决过程中,需要的图式不但要有良好的内部结构,而且要求一个图式在与其他图式相互配合使用时不会出现矛盾和冲突.也就是说,一个良构的物理图式不但具有内部的自洽性,而且和相关图式对接具有顺延的特性.简单地说,就是学习者如果构建的某一图式是良构的,那他在更上位时便能顺利地形成广域性图式.

4 结束语

问题解决是学习者在物理学习中最重要的指向之一,良构图式的获得又是学习者顺利解决物理问题的关键.在高中物理教学中,由于教师还不能普遍地、很好地指导学生建构物理良构图式,一些学生在面对情景新颖、综合性较强、能力层次要求较高的物理问题时会显得束手无策.如果这个问题不能及时得到缓解或解决,久而久之,一些学生就会对物理学习产生惧怕和抵触的心理,极端的还会放弃物理的学习.

要想较好地解决这个问题,我们首先是要分析影响学习者良构图式建构的因素是什么?影响学习者良构图式建构的因素也是多方面的,例如学习者对物理学习的态度及学习方法,教师的教学方法和学习者的数理逻辑发展水平等.当然,笔者们对其不能等量齐观,重要的是物理教学工作者应能及时、适当地加以引导,使其尽量建构起相对良构的图式.关于指导学生构建物理良构图式的有效策略,作者将会对此做进一步的探索研究.

1 John B.Best.认知心理学.黄希庭主译.北京:中国轻工业出版社,2000.397～399

2 Robert J.Strernberg.认知心理学.陈燕、邹枝玲译.北京:中国轻工业出版社,2006.199～209

3 吴庆麟.认知心理学.上海:上海科学技术出版社,2000.67～70

4 乔际平,邢红军.物理教育心理学.南宁:广西教育出版社,2002.

5 辛自强.问题解决与知识建构.北京:教育科学出版社,2005.22～38

6 Mel.S.Sabella and Edwared F.Redish.Knowledge organization and activation in physics problem soloving,Physics Education Research Section 2007(1):1017～1029