2009年高考理科综合(全国Ⅰ卷)第26题的几种解法
赵清香 王建中
(长治学院附属太行中学,山西长治 046000)
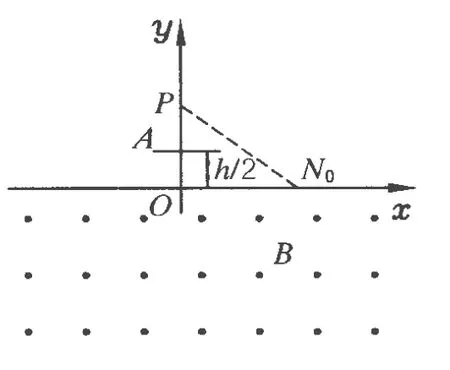
图1
题目.如图 1,在 x轴下方有匀强磁场,磁感应强度大小为 B,方向垂直于xy平面向外.P是y轴上距原点为h的一点,N0为x轴上距原点为a的一点.A是一块平行于x轴的挡板,与 x轴的距离为的中点在y轴上,长度略小于.带点粒子与挡板碰撞前后,x方向的分速度不变,y方向的分速度反向、大小不变.质量为 m,电荷量为q(q>0)的粒子从P点瞄准N0点入射,最后又通过P点.不计重力,求粒子入射速度的所有可能值.
解法1:利用通项求解

图2
如图2所示,设粒子的入射速度为 v,第 1次射出磁 场的点为 N0′,与板碰撞后再次进入磁场的位置为 N1,粒子在磁场中运动的轨道半径为 R,有

粒子速率不变,每次进入磁场与射出磁场的位置间距离 x1保持不变

粒子射出磁场与下一次进入磁场位置间的距离 x2始终不变,与 N0′N1相等,由图可知

设粒子最终离开磁场时与挡板相撞 n次,其中n=0、1、2、3……,若粒子能回到 P点,由对称性,出射点 x的坐标应为-a,即

由(3)、(4)两式,得

若粒子与挡板发生碰撞,则

联立,得

由(1)、(2)、(5)式有
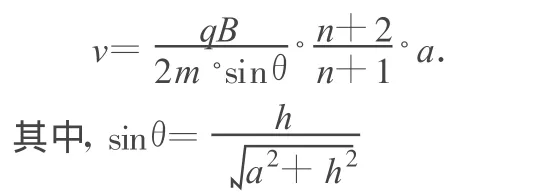
代入,得
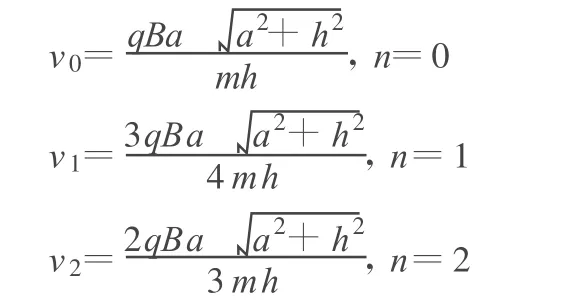
解法2:按碰撞次数分别罗列求解
设粒子的入射速度为 v,第 1次射出磁场的点为 N0′,与板碰撞后再次进入磁场的位置为N1,粒子在磁场中运动的轨道半径为 R,有

(1)与挡板不发生碰撞时,由图 3可得

由(1)~(3)式,可得

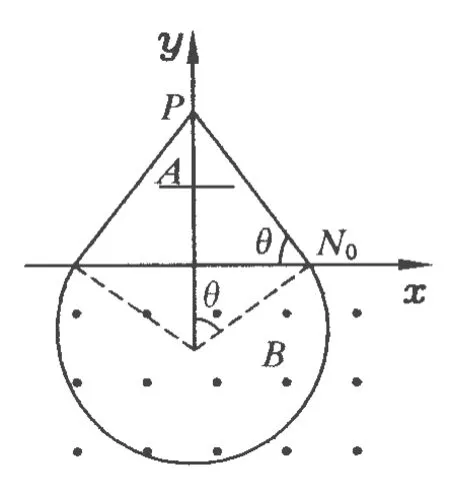
图3

图4
(2)与挡板发生一次碰撞时,由图 4可得

由(1)、(2)、(4)式,可得

(3)同理与挡板第二次碰撞时,从图 5还可得
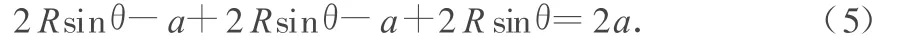
由(1)、(2)、(5)式,可得

当粒子欲与挡板第3次碰撞时,必满足
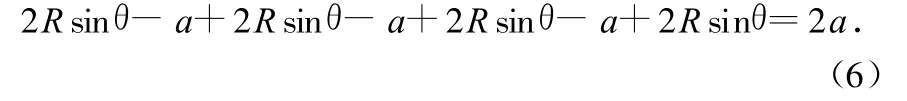
化简,得

图5

图6
如图 7,由对称性可知,粒子第 1次返回 x轴上的位置坐标可能为
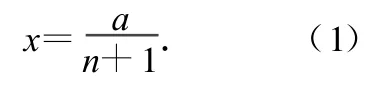
其中 n=0、1、2、3 ……为粒子打在 A板上可能的次数.
由图可得

由几何关系得
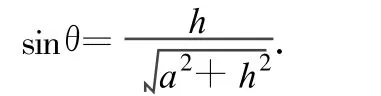

图7
(3)
将(1)~(3)式联立,可得

所以
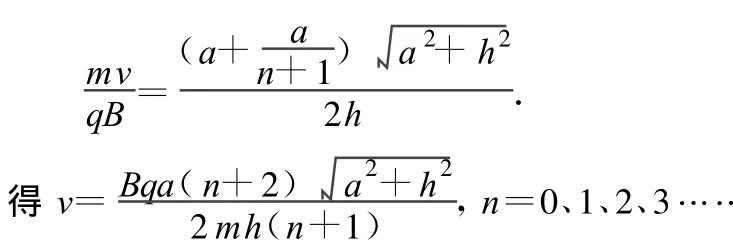
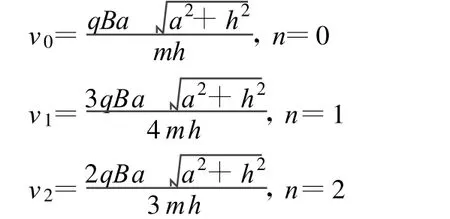
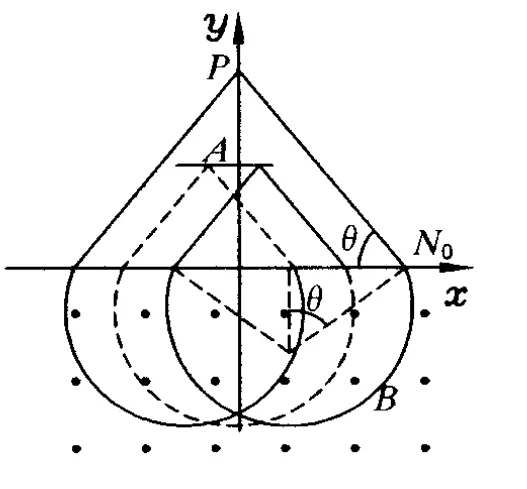
图8
解法4:通过碰撞点的横坐标求解

其中 n=0、1、2、3……
则由图 8知
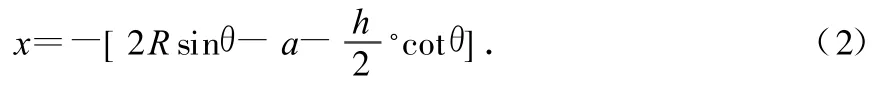
联立(1)、(2)式,得


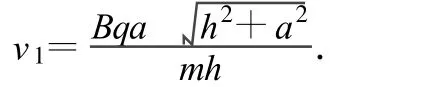
当 n=1时,碰撞点在“x=0处”,即 A板的中点,此时粒子与 A板相碰1次后回到P点,此时粒子速度


当 n≥3时,由(1)式知,粒子与 A板的碰撞点在“x≥处”,由于 A板在第 1象限最长小于故粒子将直接从 A板的右端外侧飞走,不再与 A板发生碰撞,因而n的可能取值只有n=0、n=1、n=2.

