对方案有偏好的vague集互反判断矩阵决策法
要瑞璞,沈惠璋
(1.天津商业大学 信息工程学院,天津 300134;2.上海交通大学 系统工程研究所,上海 200052)
目前,应用模糊集合对指标权重信息确定的多指标决策问题的研究比较多,并且相应的决策理论与方法已较为完善。对于vague集目前研究其相似度的方法比较多,对vague集的多指标的决策问题研究也取得了一些进展,对于权重未知且对方案有主观偏好的vague集多属性决策问题,到目前为止尚未见报道。针对此类问题,本文拟提出一种基于互反判断矩阵的求解权重方法和决策方法。该方法首先将vague值转化为模糊值,并进一步计算得到互反判断矩阵,通过计算主客观互反判断矩阵间的偏差来建立最优化模型;求解该模型得到各属性的权重,进而通过求解各方案的综合属性值对方案进行排序,得出最优方案。
1 预备知识
1.1 vague值转换为fuzzy值[1]
对于多属性决策问题,设 A={A1,A2,…,Am}为方案集,C={C1,C2,…,Cn}为指标集,各方案对应各指标下的值用vague值表示为aij=|tij,1-fij|,i=1,2,…,m;j=1,2,…,n。Vague值可按下式转换为fuzzy值:
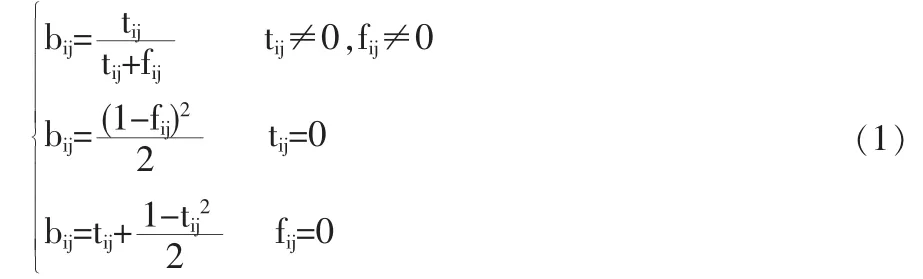
1.2 模糊效用值转换为模糊互反判断矩阵[2]
设 ui,uj分别为方案 Ai,Aj的效用值,ui,uj∈[0,1]i,j=1,2,…m,将效用值按下式转换为模糊互反判断矩阵P=(pij)mxm。

2 vague集多属性决策方法
设某一决策问题有m个候选方案A={A1,A2,…,Am};n个指标C1,C2,…,Cn;各个指标的权重用ω1,ω2,…ωn表示。方案Ai在第j个评价指标Cj下的值用vague值表示为aij=|tij,1-fij|,i=1,2,…,m;j=1,2,…,n。已知决策者对方案Ai的偏好用vague表示为 ai*=|ti*,1-fi*|,i=1,2,…,m。
(1)将各方案对应各指标的vague值aij=|tij,1-fij|,转换为fuzzy值,得到矩阵B=(bij)mxn,那么各方案的综合属性值为

(2)将决策者对方案的偏好vague值ai*=|ti*,1-fi*|转换为fuzzy值,进而构成模糊互反判断矩阵P=(pij)mxm。
(3)将各方案的综合属性值zi(w)两两比较,由(2)式可转换为模糊互反判断矩阵P 和存在一定的偏差,令则
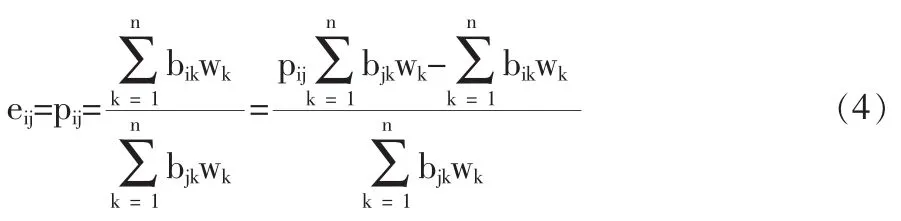
指标权重的选择应使在所有指标下偏差E最小,由此建立最优化模型:
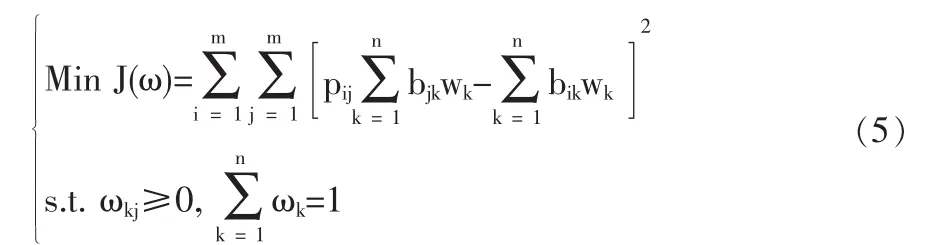
选 Langrange 函数 L(ω,λ):
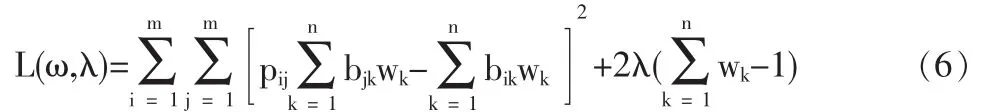
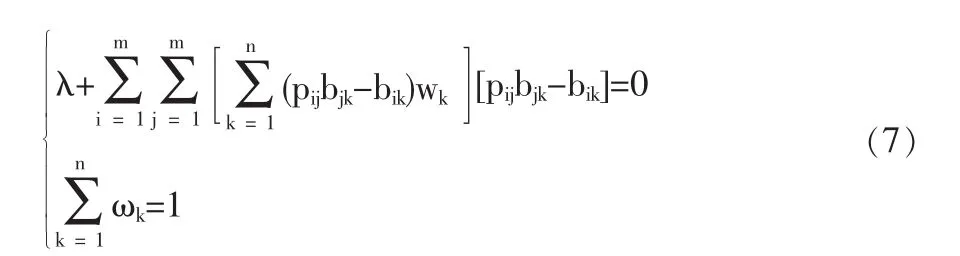
求解方程组(7)可得指标的权重 ω1,ω2,…,ωn。
(4)由各属性的权重,并由式(3)计算各方案综合属性值,对方案进行排序和择优。
3 实例分析
设某一决策问题有3个候选方案A1,A2,A3和3个评价指标C1,C2,C3,各候选方案在各指标下的特性用vague集表示如下所示,决策者对各方案的偏好为:a1*=[0.8,0.9],a2*=[0.5,0.7],a3*=[0.4,0.8]试选取最优方案。

应用Matlab计算结果如下:
(1)应用式(1)将上述vague值转换为模糊值

(2)将决策者对方案的偏好值转换为模糊值,并由式(2)转换为模糊互反判断矩阵P

(3)求解方程组(7)可得指标权重 W=[0.1357 0.4934 0.3709]
(4)计算各方案综合属性值
z1=0.5449,z2=0.3051,z3=0.3346,所以 A1>A3>A2,由此得最优方案为A1。
4 结论
本文提出的决策方法使用于属性权重未知且对方案有偏好的vague集多属性决策问题,提出了将属性vague值和偏好vague值转化为互反判断矩阵来建立最优化模型,从而求得各属性的权重,通过计算各方案的综合属性值对方案进行排序。该方法考虑了决策者偏好信息对权重的影响,评价结果较为客观,易于计算机实现。
[1]要瑞璞,沈惠璋.vague集多指标决策的模糊值线性序法[J].计算机工程与应用,2009,(6).
[2]樊治平,姜艳萍.基于OWG算子的不同形式偏好信息的群决策方法[J].管理科学学报,2003,27(1).

