采用多段杆单元的斜拉索数值模拟方法

沈旭东 高恩全 魏乐永

1 概述

近几年,相当多的跨海越江通道被列入议事日程,使建造超大跨度斜拉桥的机会越来越多,特别是在大江河口的软土地基和不适合修建悬索桥的地区,修建千米级斜拉桥的可能性更大[1]。对于一般跨径斜拉桥计算通常采用线性理论,但对于超大跨径斜拉桥中的斜拉索计算,由于垂度效应的影响,线性计算已经难以满足其精度要求,需要进行非线性计算。而直接采用非线性斜拉索模型(索单元)会导致计算速度缓慢,迭代不容易收敛,甚至使整个斜拉桥结构计算无法完成[2]。

本文针对该问题,以一座1 400 m主跨斜拉桥试设计中的斜拉索为研究对象,利用有限元技术采用多段杆单元模拟斜拉索非线性特性,包括斜拉索垂度效应、等效弹性模量以及承载效率,并将计算结果与精确解析解结果进行对比,以此确定模拟斜拉索索单元时所采用的合理多段杆单元单元数。

2 斜拉索多段杆单元模拟方法

斜拉索作为柔性构件,在自重作用下呈悬链线形状,其轴向刚度将随着垂度的变化而变化。在采用直杆单元模拟斜拉索的情况下,由于不能考虑这种变化,因此斜拉索的拉力与杆端位移之间出现了非线性关系。研究表明,拉索的垂度产生的非线性效应随自重及拉索水平投影长度的增加而增加,随拉力的增大而减小。目前拉索垂度效应的模拟主要有4种方法:等效模量法、多节点曲线索单元法、悬链线索单元法、多段杆单元法。而以有限单元法为主的数值计算中,多段杆单元以其精确方便而在实际应用中具有较大优势,见图1。

具体来说,多段杆单元法采用多个杆单元来模拟索曲线,它通过多个杆单元节点来定义索中间点的运动,从而模拟索的非线性行为。理论上,当单元数量足够多时,用分段杆单元所模拟的斜拉索的力学性态就趋于其真实的力学性态。这种方法规避了悬链线索单元刚度矩阵推导的繁琐过程,可应用现有的非线性分析程序,而且对精度的要求可以通过增大拉索分段数目得到满足,因此在应用通用有限元分析程序的结构分析中得到了广泛应用。

可以看出,多段杆单元实际应用时,如何选用单元数目是一个关键问题,它直接影响到数值计算的精度和计算消耗时间。下文中将采用该方法针对不同杆单元数目进行斜拉索计算,通过与精确解计算结果进行对比,得出合理的杆单元数目。

3 研究对象

双塔三跨斜拉桥塔高与主跨之比宜取0.20～0.25(塔高与半跨之比0.40～0.50),外索的水平倾角不小于22°。本文为不失一般性,取名义斜率为0.4的斜拉索为研究对象,并同时考虑斜拉索水平投影长度的变化。斜拉索设计参数见表1,部分参数取自一座1 400 m斜拉桥试设计。

表1 斜拉索计算模型参数表

为方便对比,将同时采用解析解对其进行精确解计算,所采用解析解公式见表2,详细的推导过程可参见相关参考文献[3]。

多段杆单元采用ANSYS有限元软件进行数值计算,解析解采用MATLAB数学软件进行数学计算。

4 计算结果及对比分析

按上一节介绍的研究对象,分别按不同多段杆单元单元数(20,15,10,5,3)对斜拉索关键力学特性(名义斜率与实际斜率之差、垂度效应、等效弹性模量)进行计算,并与精确解进行对比,计算结果如图2所示。

图2中横坐标代表斜拉索水平投影长度自50 m变至5 000 m,纵坐标分别代表所研究的斜拉索关键力学特性。由图2可以得出以下结论:

1)斜拉索关键特性随跨径增大变化很大,所以对斜拉索计算的精度的要求会随斜拉索跨径的增大而相应提高。

2)3或5 单元多段杆单元在整个斜拉索研究跨径内都与精确解差距较大,特别当斜拉索水平投影长度超过1 000 m之后,计算结论几乎无法使用。

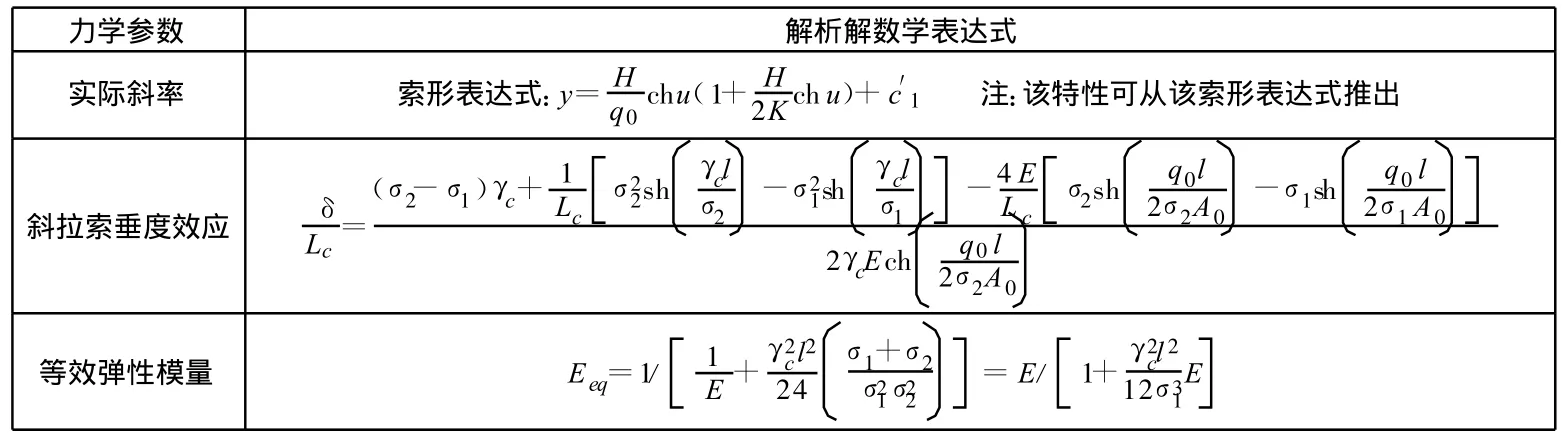
表2 斜拉索精确解析解

3)20或15 单元多段杆单元在整个斜拉索研究跨径内都与精确解差距较小,可以说几乎与精确解计算结果一致,但因此所增加的计算时间以及迭代收敛困难程度却相应大幅度增加,特别在工程设计中计算成本过大。

4)10单元多段杆单元在精度与计算时间之间取得平衡,既保证了可以接受的精确度,又没有增加过多的计算时间亦没有增大迭代收敛的难度,可以说在整个可能使用的斜拉索跨度中,10单元多段杆单元是一个理想的计算斜拉索的有限元计算单元。

5 结语

本文针对50 m～5 000 m斜拉索,采用不同杆单元数目的多段杆单元对斜拉索关键力学特性进行了数值计算,并将计算结果与精确解进行对比,得出采用10单元多段杆单元模拟斜拉索是一个理想的有限元简化方法,该数目多段杆单元既保证了计算精确度,又没有增加过多的计算时间。

[1] 严国敏.现代斜拉桥[M].成都:西南交通大学出版社,1996.

[2] 孟庆成,齐 欣.千米级斜拉桥斜拉索相关参数计算方法[J].桥梁建设,2009(2):18-19.

[3] 李强兴.斜拉索静力解[J].桥梁建设,1996(3):21-25.