基于灰度形态学梯度的边缘检测
武 毅,李仰军,李 忠
(1.中北大学信息与通信工程学院,山西太原030051;2.河北南风汽车设备集团有限公司,河北沧州061503)
0 引言
数学形态学是图像处理一门新兴学科,具有严格的数学理论基础,现己在图像工程中得到了广泛应用[1]。基本思想是用具有一定形态的结构元素去度量和提取图像中的对应形状以达到对图像分析和识别的目的,获得的图像结构信息与结构元素的尺寸和形状都有关系,构造不同的结构元素,便可完成不同的图像分析。数学形态学包括二值形态学、灰度形态学和彩色形态学;基本变换包括膨胀、腐蚀、开启、闭合四种运算,并由这四种运算演化出了开、闭、薄化、厚化等,从而完成复杂的形态变换。目前灰度形态学在边缘检测中的应用越来越引起人们的关注并逐渐走向成熟。
在形态学中定义了两个基本的变换,即腐蚀和膨胀。一般将形态学变换作用于实际图像的过程称为形态学运算。设一幅灰值图像,其中(x,y)为图像上点的坐标,f(x,y)为(x,y)处的灰度值。灰值图像的腐蚀、膨胀运算的定义如下:

图1 太阳能电池板表面裂纹原图
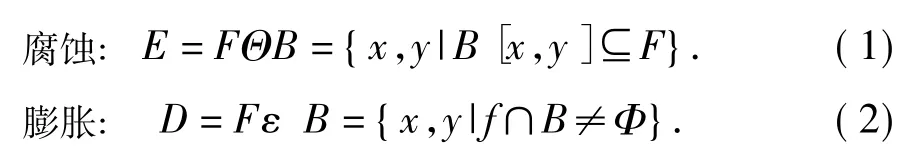
1 灰度形态学
数学形态学首先处理二值图像。数学形态学将二值图像看成是集合,并用结构元素来探察。灰度数学形态学是二值数学形态学对灰度图像的自然扩展。

图2 灰值图像的腐蚀
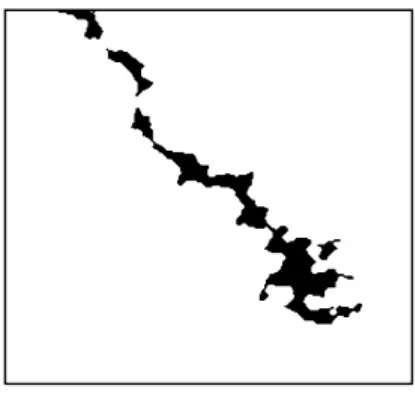
图3 灰值图像的膨胀
文中采用基于数学形态学梯度的图像边缘检测算法[2],利用数学形态学的基本运算,设计符合处理图像边缘特性的梯度结构基来检测局部突变信息从而获得图像的边缘信息。实际应用中绝大多数遇到的是灰度图像,如医学图像,遥感图像、照片等,因此有必要将二值形态学推广至灰度图像的处理。在二值形态学的基础上,我们可以方便地建立起灰度形态学的运算法则。与二值形态学不同的是,灰度图像形态学中的操作对象是数字图像函数而不是集合,而结构元素本身也可看作是一个子图像函数。在灰度图像形态处理中,输入和输出的图像都是灰度级形式的,这意味着输入和输出像素值是在最低灰度值到最高灰度值之间。
图像的边缘对人的视觉具有重要意义。边缘反映了图像的最基本特征,对边像检测算法的研究也一直是图像处理中探讨的热点问题之一。文中采用基于灰度数学形态学梯度的图像边缘检测算法,利用数学形态学的基本运算,设计符合处理图像边缘特性的梯度结构基来检测局部突变信息从而获得图像的边缘信息。
2 形态学梯度边缘检测算子
在图像边缘检测处理中,有多种梯度,若在某一像素点的梯度值大,表示在该像素点图像的获度变化迅速,从而判断出可能是边缘点。经典图像边缘检测往往采用差分梯度算子与阈值技术结合的方法。而数学形态学边缘检测方法主要利用形态学梯度完成图像的边缘检测。开运算滤波器在处理图像中仅能通过与结构元素形状一致的部分。若将形态学的腐蚀、膨胀、开运算以及闭运算等基本运算用于图像处理,可构造出形态学梯度算子,用于数字图像检测。常用的形态学梯度算子:

3 基于灰度形态学梯度的边缘检测
形态学边缘检测算子是一种非线性差分算子,在以上定义的梯度算子中,腐蚀运算经运算可以滤去图像中比结构元素小的亮细节;而保持图像整体灰度和大的亮区域基本不受影响。为此,文中采用边缘稳测算法[3,4]:
(1)对数字图像进行闭运算,然后进行开运算,实现对图像的预处理,以滤除图像中的噪声。即:

(2)将步骤1得到的图像作闭运算,实现图像的平滑运算即:
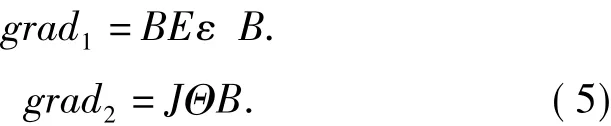
(3)求出grad2grad1之差,得到较好的边缘
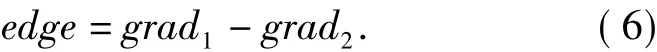
(4)重建图像

图4 灰度形态学梯度处理后的图
4 结束语
经典算子能够检测出定位比较准确并且清晰的边缘,但是边缘很多地方都有断裂,细节方面也不够完整;经典算子一般都对噪声很敏感。与经典算子相比,数学形态学方法检测的边缘完整、平滑而且连贯,几乎没有断裂的情况。形态学既有自己的滤波去噪方法,也可以直接使用形态学抗噪型算子。因而有一定的实用性。
[1]陈虎,周朝辉,王守尊.基于数学形态学的图像去噪方法研究[J].工程图学学报,2004(2):1162 -1191.
[2]阮秋琦.数字图像处理学[M].北京:电子工业出版社,2001.
[3]龚炜,石青云,程明德.数字空间中的数学形态学——理论及应用[M].北京:科学出版社,1997.
[4]Chen T,Wu Q H,Torkaman R R,et al.Apseudotop-hat Mathematical Morphological Approach to Edge de2tection in Dark Regions[J].Pattern Recognition,2002,35:199 -210.

