紧凸超曲面在一类带外力场的平均曲率流下的收缩

刘艳楠

(北京工商大学 计算机与信息工程学院, 北京 100048)

1 带外力场的平均曲率流

在这篇文章中我们主要研究

(1)

这里

Ft:=F(·,t):M→Rn+1,

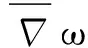
这个流推广了著名的平均曲率流(也就是ω≡const的情形)，它来自于对非均匀Ginzburg-Landau超导方程漩涡运动的研究，详见文献[2-3]， 我们称之为带外力场的平均曲率流. 关于这类流我们做了一系列的研究，并给出了光滑解长时间存在近乎最优的条件，详见文献[1]和文献[3-6].

在文献[1]中作者证明了下面结论：

本文对上面定理结论做了更细致的研究，证明当初始曲面是严格凸时，曲面在有限时间内收缩为一点，即下面定理：

定理2令

(2)

如果c<0是一个常数，且若M0是严格凸的，则当t→T时，曲面收缩为一点.

我们主要利用Huisken在文献[7]中的方法对定理 2 进行证明. 在第二节我们做些必要的准备工作，并将在第三节给出定理2的证明.

本节最后我们想指出，平移解作为平均曲率流的特解对平均曲率流的研究有着重要的研究意义，详见文献[8-9]. 而关于带外力场的四阶曲线流的研究见文献[10].

2 准备工作

本节我们给出一些曲率量的发展方程，为定理2的证明准备.

命题1 在流(2)光滑解存在时间内，平均曲率H、第二基本形式平方|A|2和体积元dμt的发展方程为：

(3)

(4)

(5)

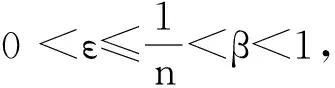
注：这个定理说明流(2)在解的存在时间内，总有H>0成立.

证明： 令

Mij=hij-εHgij,

则有

记

Nij=-2hilhljf+(|A|2-c)Mij+2εHfhij.

对Mij的零特征向量X，即MijXiXj=0，有

hijXiXj=εH|X|2,hijXi=εHXj.

利用这些关系我们可以得到

MijXiXj=0.

因此由Hamilton张量极值原理[11]，我们证明了hij≥εHgij是保持的，用同样的方法我们也可以证明hij≤βHgij是保持的.

证明： 由(3)和(4)可以得到

而

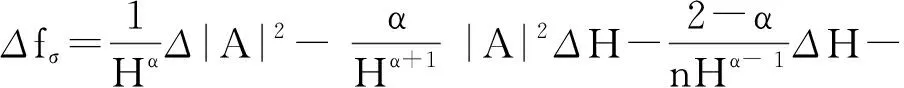
注意到

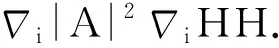
那么由这几个式子可以得到我们想要的结果.

下面我们需要Huisken文献[7]中的一个引理：

引理1 若H> 0，且对ε> 0，有hij≥εHgij， 则有

引理2 对0<α=2-σ，下面不等式成立

综合上述结果并利用文献[7]中Huisken证明定理5.1 的方法可以得到下面定理.

定理4的证明完全类似于文献[7]中定理5.1的证明，这里就不再重复，只是要注意到c<0以及Mt的体积是一致有界的事实.

引理 3

证明：利用(3)可得

又由于

故有

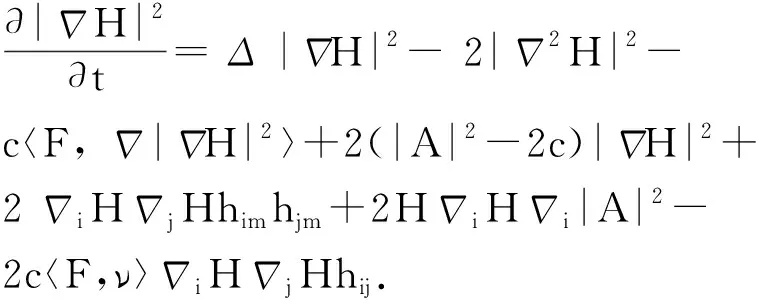
再利用Cauchy-Schwarz不等式可得所要结果.

引理4

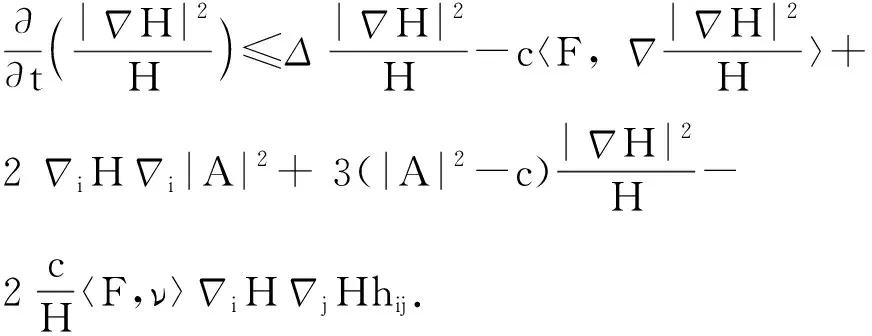
证明：利用引理3 可得

由于

所以

(6)

把它代到(6)即得结论.

引理5

(7)

(8)

这里C1仅与C0，n和δ有关.

证明：不等式(7)可由(3)容易得到. 下面证明(8). 由(3)，(4)以及(7)， 可以得到

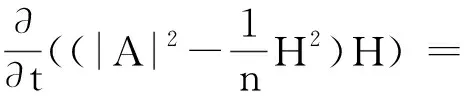
另外，因为H>0，我们有下面关系

利用定理4 可得

又由文献 [7]中引理2.2有

至此引理证毕.

定理5 对任意η>0存在常数C(η,M0,n)，使得

证明：我们考虑下面的函数

另一方面由定理3得

因此

定理得证.

3 定理2的证明

由于在文献[1]中我们已经证明了在定理2的条件下流(2)光滑解存在于有限时间区间，故我们只需再证明曲面要收缩为一点即可. 这里我们始终令Mt是流(2)在 [0,T)上的光滑解. 我们主要利用Huisken在文献[7]中的方法，证明当t→T时，diamMt→0，这一证明关键是得到关于Hmax(t)/Hmin(t)的估计.

定理6 当t→T时，Hmax(t)/Hmin(t)→1.

定理6的证明需要用到下面定理：

定理7 (见文献[7])在M上，若沿着长度至少为πK-1/2的测地线有Rij≥(n-1)Kgij，则这条测地线具有共轭点.

我们还需要用到下面引理，它的证明可由Rij=Hhij-hilhlj容易得到：

引理6 在M上，如果对0 <ε≤1/n，有hij≥εHgij成立， 则Rij≥(n-1)ε2H2gij.

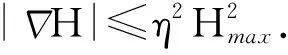
(9)

另外，根据引理6和定理7，可得在Mθ上

Hmin≥(1-η)Hmax.

(10)

又由于Hmin是非减的，故

Hmin(t)≥1/2Hmax(θ),θ≤t

因此，不等式(9)和(10)对所有θ≤t