L-拓扑空间中的Ⅲ型强连通集
刘孝力,刘 琳
-拓扑空间中的Ⅲ型强连通集
刘孝力,刘 琳
(五邑大学 数理系,广东 江门 529020)


1 引言与预备知识
2 L-集的Ⅲ型强连通集
证明 容易证出.
证明 显然.
证明 显然.
证明 与文献[3]中定理2. 9的证明类似.
推论2.9 若一族Ⅲ型强连通集的交非空,则它们的并是Ⅲ型强连通集.
由预备知识中的结论可得:


必要性. 设定理中条件不成立,即存在映射
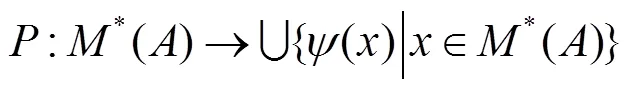
3 与其它强连通之间的关系

致谢 感谢白世忠教授的悉心指导!
[1]王国俊.-fuzzy拓扑空间中的连通性[J]. 陕西师范大学学报:自然科学版,1987(3): 1-10.
[2] BAI S Z. Strong connectedness in-fuzzy topological spaces [J]. J Fuzzy Math, 1995, 3: 715-719.
[3] BAI S Z, WANG W L. I type of strong connectivity in L-fuzzy topological spaces[J]. J Fuzzy Set and Systems, 1998, 993: 357-362.
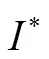
[5] BAI S Z. PS-connectedness of L-subsets[J]. J Korean Math Soc, 2007, 44(1): 129-137.
[7] LIU X L. Fuzzy WS-irresolute mappings[C]//The third intelligent computing conference. Jinan: global Link publisher, 2009.
[8]王国俊. LF拓扑空间论[M]. 西安:陕西师范大学出版社,1988.
[9]PAO B M, LIU Y M. Fuzzy topology I[J]. J Math Anal Appl, 1980, 76: 571-599.
[责任编辑:熊玉涛]
A New Kind of Connectedness in-Topological Spaces
LIUXiao-li,LIULin
With the help of the weakly semiclosed sets, we introduce the concept of Ⅲ type of connectivity in-topological spaces and study Ⅲ type of connectivity properties and other type of connectivity connection in-topological spaces.
-topological spaces; weakly semiclosed sets; weak semiclosure; connected sets.
1006-7302(2010)01-0052-05
O189.1
A
2009-05-14
广东省自然科学基金资助项目(8152902001000004),江门市科技计划项目(江财工[2008]103)
刘孝力(1980—),男,河南民权人,在读研究生,研究方向:格上拓扑学,E-mail: abcxiaoliliumn@163.com.

