改进的海浪波包谱

刘 思，柳淑学，俞聿修

（大连理工大学海岸及近海工程国家重点实验室，大连116024）

海浪群性是海浪场的一种重要特性，对海堤、港湾共震、系泊浮体运动等有明显影响。关于波群研究的波包线理论认为，波群即波列局部振幅（或称波面包络，简称波包）随空间和时间缓慢变化的现象，用波包来讨论波群方便而直接。现有研究表明，海浪群性的大小与其波包谱（包线谱）的形状大小密切相关。目前对波谱已进行了大量的研究，得出了多种实用成果，但对于海浪的波包谱研究较少。

Tayfun等［1］讨论了波包谱与波谱的关系，给出波包谱的理论形式。Xu等［2］将波包谱的概念用于波群模拟中，建立了以给定波谱和波包谱为靶谱的波群模拟方法，认为波群特征可由波谱和波包谱两者决定，然而其方法并未得到实用的波包谱，所建议的波群特征参数也不合理，难以应用于实际。俞聿修等［3］采用了合适的波群特征参数，首次提出了风浪波包谱的经验公式，但所依据的实测波浪资料较少，有些假定不尽合理，还需进一步的验证和改进。

鉴于此，本文收集了更多的实测波浪资料，一方面计算实测波浪的群性特征参数并对其相关性进行分析，另一方面计算实测波浪的波包谱，从中总结规律，以期得到一个更能反映天然海浪的波包能量分布的波包谱经验公式。

1 实测波浪资料的群性特征参数分析

关于波群的研究中，基于瞬时波能过程线（SIWEH）［4］、连长理论［5］和波包线理论［6］定义的参数得到了广泛应用。这些参数一般从两方面描述波浪群性：一方面是描述波群的高度特性，如参数GF，GFA，GFH等；另一方面是描述波群的长度特性，如GLF。其中GF是Funke等［4］提出的用SIWEH定义的参数，定义式为

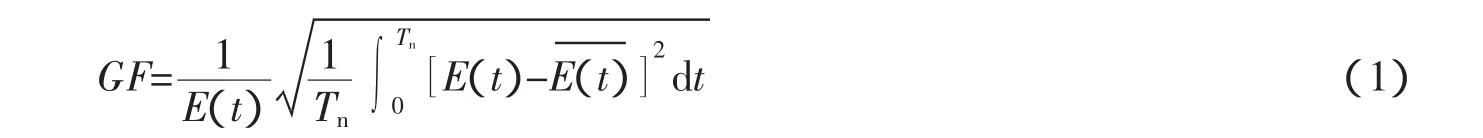
式中：Tn为波浪资料的总长度；E（t）为光滑瞬时波能过程线，定义为

式中：η为波面记录；Q（τ）为光滑函数，可采用Barleet窗，即

式中：Tw为窗口长度。GFA为List［6］由波包线出发定义的，先将波面记录η（t）滤去小于0.05 Hz的低频波，然后对进行低通滤波，滤去原始波面，得到波面包线，进而定义波群因子式中σA和分别为波包线的方差和均值。GFA为一个无量纲参数，且分布在0～1。但上述计算波包线的方法明显地受到滤波截止频率的影响。GFH是俞聿修等［7］建议的描述群高的参数，其定义式与GFA相同，二者区别在于计算GFH时，其波包线是通过Hilbert变换由波面记录直接计算得到，不需进行滤波。GLF是波谱的峰频fp与波包谱峰频fpA的比值［7］，所以GLF越大，波包线的周期相对于波周期越大，即波群越长，GFH和GLF的计算公式可写为

Goda［5］按上跨零点顺序确定各个波浪的波高，定义超过某个预定门槛值的波群为连，连内的波数称为连长，用1表示。

目前常笼统地将波群的高度特征参数如GF或GFH，作为判定群性大小的依据，而事实上群高参数的大小与波群的长度特征并非一一对应。尚不清楚群高大的海浪，其群长是否也一定大。因此，有必要对这两者之间的关系进行研究。

对美国西海岸、中国珠江口和渤海3个测站的实测波浪资料进行波群特征参数的分析，为推导波包谱经验公式作准备。其中美国西海岸外海观测资料有4组［7］，每组采集点数18 000个，测点水深为2 100 m，采样时距为0.39 s，时长约117 min，H1/3=2.34～2.92 m，T1/3=14.6～15.3 s；珠江口实测波浪资料由底压式测波仪测得，水深约10 m，采样频率4 Hz，每次采样4 800个点，时长约20 min，选用的71组波浪主要波要素H1/3=0.50～1.58 m，T1/3=2.79～5.25 s；渤海实测波浪资料是由垂线测波仪在水深27 m处测得，采样频率4 Hz，时长约20 min，选用的26组波浪主要波要素为H1/3=0.62～2.54 m，T1/3=3.65～6.34 s。图1给出这三地海浪资料的主要波群参数计算结果，并对参数的联合分布作了线性回归分析，图1中实线是按最小二乘法作的线性拟合，其线性回归方程拟合的相关系数及标准差已注明。除了可以获悉对于实测海浪资料来讲，其波群参数的主要分布范围外，从图1-a可以看出，群高参数GFH和GF的相关性较好，而图1-b表明GFH和群长参数GLF的相关性较差，如当GFH=0.7时，GLF的取值大约可由5变化到25。同样，从图1-c可以看出，GFH和群长参数1的相关性也不好。由此可见，描述海浪群性高度特征的参数与描述其长度特征的参数的相关性不强。

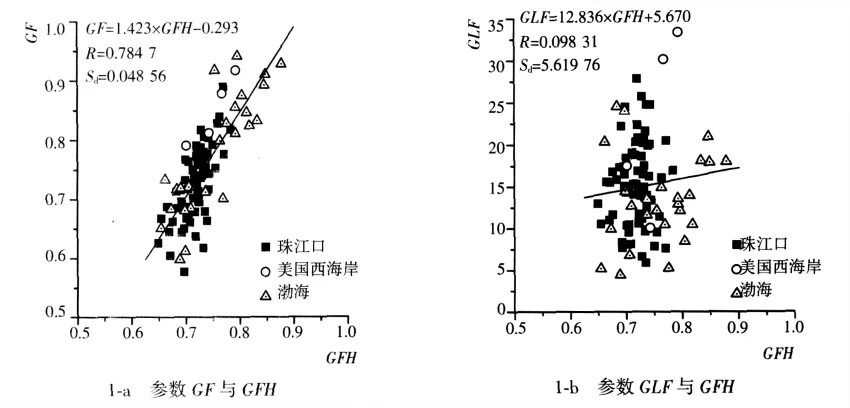
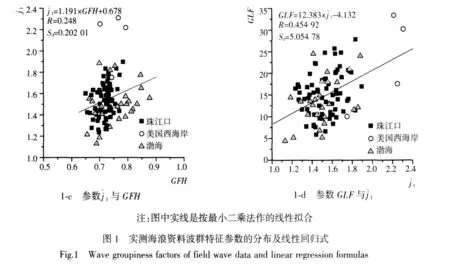
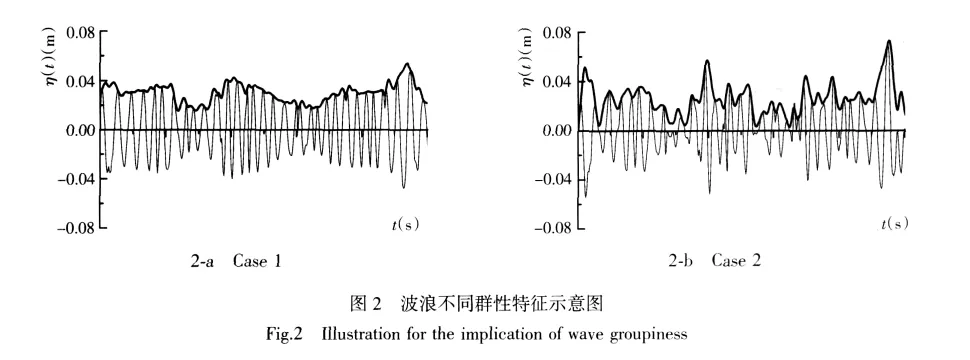
图2给出了2组具有明显不同群性特征波列的示意图。图2-a中由波包线定义的每个群内包含多个大波，波包线平坦，图2-b中按波包线定义的每个群内的大波个数少，波包线起伏变化较快。可以看出，群性的不同主要体现在波包起伏幅度和变化快慢的不同，群高主要表征波群内外波振幅的差别，其统计特征量反映波包的起伏幅度，群长主要表征波群内大波个数，其统计特征量反映波包的变化快慢，或者说是连续大波的持续长度。显然，图2-a中群长大而群高小，图2-b中群长小而群高大。由此可以推断，正如描述波面的统计特征量波高与周期，在一定范围内的相对独立性一样，描述波群的高度特征参数与长度特征参数也是从不同角度描述海浪群性的大小，是在一定范围内相对独立的参量。

事实上，波群的高度特征和长度特征都是海洋工程所关心的。因此在关于海浪波群的研究中，至少需要给出2个参数来表征波浪群性的大小。对于如何定义这2个参数的问题，List［6］充分阐述了无论是基于SIWEH定义的GF，还是波包线定义的群因子GFA，都对窗口长度值的选取很敏感，参数GF的另一个缺陷是没有限定范围，有的波群GF参数值比1.0大得多。相比之下，据波包线理论定义的波群参数GFH有明确的变化范围（0～1），且不受滤波的影响。另一方面，平均连长j¯1是某个门槛值下波列内各个波群中包含波数的平均值，可按Kimura［8］考虑相邻波高间相关性的波浪连长概率理论算得。俞聿修等［7］对渤海风浪和日照港资料平均连长的统计分析值与计算值进行了比较分析，发现按Kimura理论计算的平均连长值与实测值符合良好，而且与群高因子、谱的尖度参数Qp等［9］有较好的相关性。但该参数不是以谱的形式定义的，不便于应用［10］。而参数GLF为波谱与波包谱的峰频之比，应用方便，且与群长参数1有一定的相关性，从本文用到的实测波浪资料统计分析结果看，相关系数接近0.5（图1-d）。在下文中采用参数GFH和GLF来共同表征波浪的群性特征。

2 实测波浪资料的波包谱分析

俞聿修等［3］根据渤海实测波浪资料进行波包谱分析，发现波包谱基本呈单峰形，且谱形尖而窄，峰频非常小。对波包谱无因次化时，纵坐标取y=SA（f）/m0A，横坐标取x=f/fPA，其中fPA为波包谱的峰频，SA（f）为波包谱密度，m0A为波包谱的零阶矩。这样得到的“无因次”波包谱的峰频为1，峰值基本上趋于一致（约等于20），从而对无因次化后的谱可以频率f=fPA为界限分2段给出拟合公式

假定波浪为平稳，窄谱随机过程，波高符合瑞利分布，则有

式中：m0为波谱的零阶矩，又据式（4）群高参数GFH的定义，可推得

将式（8）代入式（6），从而给出了一个初步的波包谱经验公式

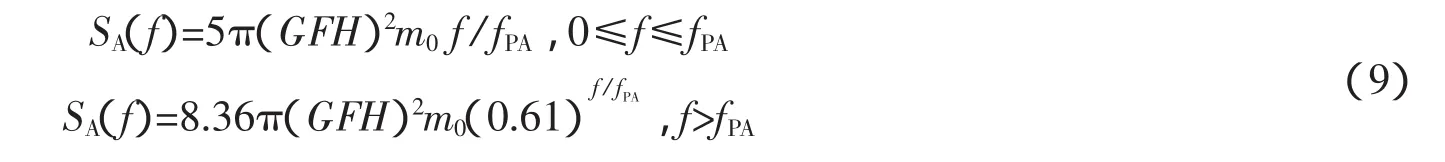
式（9）中fPA按下式确定

然而，此波包谱经验公式是仅依据渤海实测波浪资料得到的，虽适用于渤海资料情况，但存在下列3个主要问题。

（1）按上述无因次化方法，对珠江口实测波浪资料计算得到的各“无因次”波包谱的峰值相对较离散（图3）。说明对于更多更广的实测波浪资料，此经验公式的适用性值得商榷。

（2）依据图1-b给出的实测波浪资料的群性参数GFH和GLF的分布可知，公式中给出的群高参数GFH与fPA的取值不尽合理。

（3）给定相同的m0和参数GFH时，不考虑式（10）的限制，按式（9）计算得到的波包谱随参数GLF变化情况见图4。从图4可以看出，随GLF参数值的减小，波包谱峰频增大，其面积也增大，这与推导过程中用到的式（8）矛盾，其原因是对波包谱无因次化时，纵坐标取的是y=SA（f）/m0A，并没有实现完全的无因次化。

根据上千组珠江口和渤海两地的原始波浪观测资料，对上述波包谱经验公式进行改进。考虑到波包谱与波浪群性特征的密切关系，以及波群的高度特征和长度特征在一定范围内相对独立的特点，希望得到的波包谱经验公式同时包含群高参数和群长参数。首先对原始资料进行滤波处理（主要去除波浪过程中的高频干扰），然后应用Hilbert变换方法，由处理后的波面记录计算波包线，对于窄谱海浪，波面η（t）的Hilbert变换定义为

式中：P为当t=τ时积分取Cauchy主值。波包可由下式计算

再对波包线进行传统的傅立叶变换，从而得到波包谱。注意到波包谱的峰频很小，计算时频率划分间隔必须足够小，以保证计算谱及参数GLF的准确性。最后，按照波浪有效波高值大于0.5 m，且计算频谱是单峰的原则，共筛选出97组波浪的波包谱来分析。对所选的97个波包谱进行无因次化，具体无因次化的方法是

无因次化后的结果以黑点绘于图5中。由图5可以看出，尽管由于波浪资料的统计可变性，峰值及峰值两侧的曲线分布较离散，各无因次波包谱有近似的趋势。为寻求总体上的规律，先对这97个波包谱求一个平均谱，再无因次化，将其结果也绘于图5中（见图5中白色曲线）。以谱峰为分界点对这条曲线的两边分别拟合，因谱峰的左侧频带窄，曲线很陡，故直接取直线y=a+bx来近似，而右侧可以用曲线y=Aexp（-Bx）拟合，依此得到拟合公式为

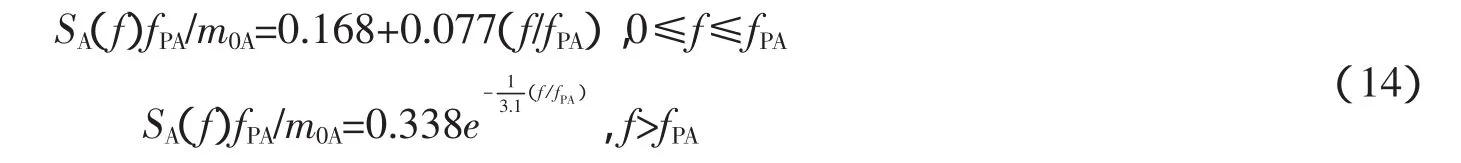
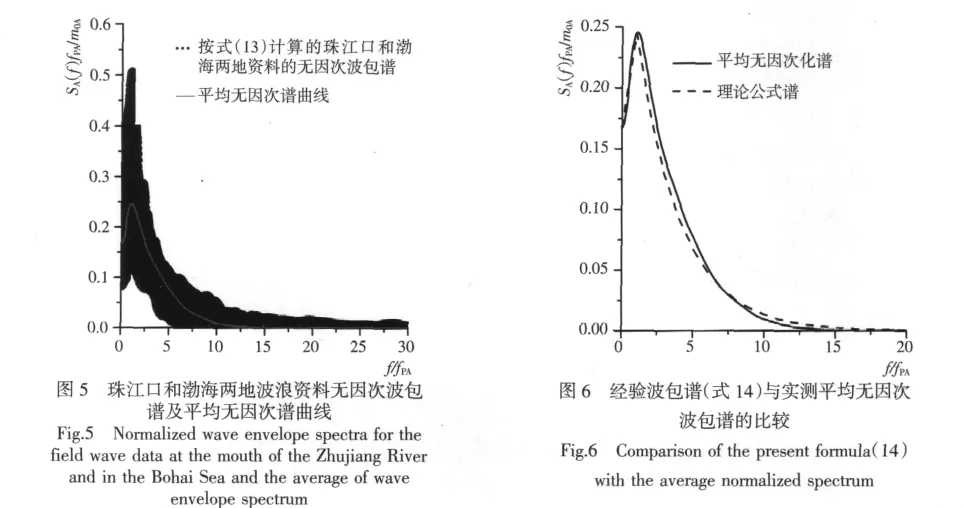
图6中虚线是按式（14）绘出的经验无因次波包谱，实线是实测资料的平均无因次波包谱，从图6上看，二者基本一致。由此可见，对图5中白色曲线采用式（14）拟合是可行的。将式（8）代入式（14），可得到用f表示的有因次波包谱经验公式

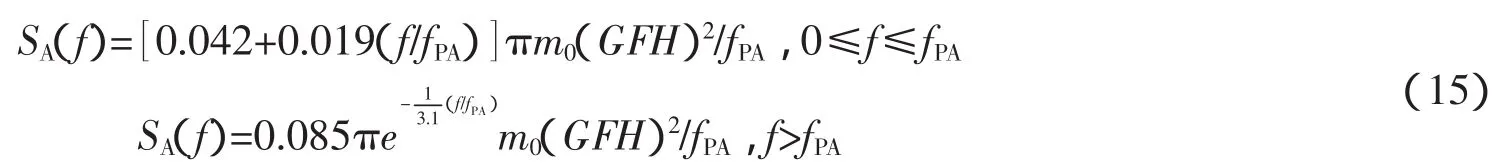
从式（15）可以看出，若已知波谱，通过给定fPA和波群参数GFH就可以计算得到波包谱SA（f）。式中的fPA可由给定的群长参数GLF确定，根据前述波群特征参数的分析，实际海浪的群长参数GLF大多分布在5～28，群高参数GFH多集中于0.5～1变化。尽管二者的相关性较差，但如同波高与周期的联合分布一样，群高与群长具有一定的相关性，建议fPA按下式确定

图7和图8给出波谱一定时，改变群高参数GFH或群长参数GLF对此经验波包谱的影响。从图7可知，GLF不变时，随着给定群高参数GFH增大，波包谱峰值增大，相应地波包谱零阶矩增大；从图8可以看出，GFH不变时，随着给定群长参数GLF的增大，波包谱峰频减小，峰值增大，而波包谱零阶矩基本不变。这正如所预期的，GFH表征波群的高度，其变化会改变波包络的平均能量，即波包谱的零阶矩，同时，GLF表征波群的长度，其变化会改变波包谱峰频，而不影响其零阶矩大小。

此外计算了美国西海岸4组实测波浪资料的波包谱，其无因次波包谱也分布在图5所示的范围内，且谱形与之相近，因其波浪性质是以涌浪为主的混合浪，因此推测式（15）和式（16）还可适用于涌浪为主的混合浪，有待于更多的实测资料来检验。

至此，式（15）和式（16）可建议作为一个适于风浪的波包谱经验公式。该公式的特点是只包含波要素和波群参数作为参量，便于工程应用，且同时考虑了群高与群长两方面的因素。与俞聿修等［3］所给定的经验公式（9）和式（10）相比，本文建立的波包谱经验公式推导过程中采用了更合理的无因次方法，依据3处海区的波浪观测资料，其结果具有普遍性，据实测波浪资料群性特征参数的分析结果，公式中参数的取值原则也较为合理。

3 结语

本文对大量实测波浪资料进行了波浪群性特征参数分析，结果表明，群高与群长相关性很小，在此基础上对俞聿修所建议的波包谱公式加以改进，给出了一个适于风浪的波包谱经验公式。该公式同时考虑了群高与群长两方面的因素，只要给出波要素和波群的特征参数GFH和GLF，便可确定波包谱形，依据对实测资料波群参数的分析结果，给出了较合理的参数取值原则，便于应用，为波群的模拟提供了较好的基础。

［1］Tayfun M A，Lo J M.Wave envelope and related spectra［J］.Journal of Waterways Port Coastal and Ocean Eng.，ASCE，1989，115：515-533.

［2］Xu D L，Hou W，Zhao M，et al.The statistical simulation of wave groups［J］.Applied Ocean Research，1993，15：217-226.

［3］俞聿修，桂满海.波群的数值模拟和物理模拟［J］.大连理工大学学报，1998，38（1）：86-91.YU Y X，GUI M H.Numerical simulation and physical simulation of sea wave groups［J］.Journal of Dalian University of Technology，1998，38（1）：86-91.

［4］Funke E R，Mansard E P D.On the synthesis of realistic sea states in laboratory flume［C］//ASCE.Proc.17th Inter.Conf.on Coastal Engineering.Sydney：［s.n.］，1980.

［5］Goda Y.Numerical experiments on wave statistics with spectral simulation［R］.Rept.Port and Harbour Res.Inst.1970，9（3）：3-57.

［6］List J H.Wave groupiness variations in the near shore［J］.Coastal Engineering，1991，15：475-496.

［7］俞聿修，桂满海.海浪的群性及其主要特征参数［J］.海洋工程，1998，16（3）：9-21.YU Y X，GUI M H.Groupiness of sea waves and their characteristic parameters［J］.The Ocean Engineering，1998，16（3）：9-21.

［8］Kimura A.Statistical properties of random wave groups［C］//ASCE.Proc.I7th International Conf.on Coastal Engineering.Sydney：［s.n.］，1980.

［9］俞聿修.随机波浪及其工程应用［M］.大连：大连理工大学出版社，2000.

［10］Masson D，Chandler P.Wave groups：a closer look at spectral methods［J］.Coastal Engineering，1993，20：249-275.