数值模型在水工建筑物分析中的应用

[巴西] R.格鲁伯 等

三维紊流及其数学表示的复杂特性常常要求采用物理模型模拟水工建筑物的水力条件并确定设计参数。随着计算机能力的增强,与物理模型相比,数值模型越来越强大。它们能更加经济、灵活和快速地生成设计信息。但是,许多水工设计人员对用数学推导参数来定义水工建筑物设计所需的相关水流特性数值的完整性和精确性仍存有疑问。本文介绍了建立数值模型的 2个实例,并将其结果与相应的物理参数进行了比较。实例研究为:

(1)巴西托坎廷斯河上在建的圣萨尔瓦多水电工程的溢洪道,为便于比较沿溢洪道建筑物的实测平均压力和数值模型的相应结果,建造了常规的溢洪道物理断面模型。

(2)墨西哥普雷西迪奥河上在建的皮卡乔斯灌溉坝的溢洪道,收集了物理模型有关出流能力和一般水流条件的信息,并与数值模型进行了比较。

1 数值模型特性

基于求解纳维叶 -斯托克斯方程的有限体积法,采用商用软件包 FLOW-3D对溢洪道水流进行数值分析。用该软件可模拟永久或暂态条件下的三维水流。选择该软件的原因在于:

(1)能模拟具有复杂固体边界的三维水流,甚至在用正交网格工作时都不例外;

(2)适合于模拟不可压缩自由面水流,当然,对于模拟本文所列举的实例,这是一个重要特性。

有限体积法利用一个单元(体积)的质量和运动之间的平衡来求解纳维叶 -斯托克斯方程。因此,一组方程的解可能确定每个单元的速度和压力值。通过将连续的时间函数转换为离散的间隔,该软件采用在规定时间周期提供渐进解的显式方法。它详细描述了后续的时间步长,但是,出于数值稳定性打算,以非常小的时间增量为条件。为了提高主要是固态边界处的网格精度,该软件可以采用多块技术。对于本文分析的实例,采用了正交网格。

采用常规设计软件所建立的三维模型获得建筑物和天然地域的几何形态,所用的紊流模型是一种方程法和k-ε,对于三维水流可获得很好的结果,没有过多地增加处理时间。

将上游(水库)水位、对应的下游(尾水)水位和对称条件作为边界条件。

2 圣萨尔瓦多工程的溢洪道

巴西托坎廷斯河上的圣萨尔瓦多水电工程正在施工中。闸控溢洪道按 10000 a一遇洪水设计,相应的流量为19300m3/s。溢洪道包括 6扇宽15.4 m的闸门,堰顶高程为 265 m。为下泄设计洪水,水库水位上升到287.3m,产生22.3 m的堰顶水头。通过一座长60.0 m、宽112.4 m的水跃消力池消能。

在设计上,溢洪道尺寸按照美国垦务局和美国陆军工程师团的通用标准确定。为验证水流条件和为结构设计提供依据,在巴西巴拉那大学CEH PAR水工实验室建造了 2个物理模型。第 1个为工程整体模型,比例为 1∶100,按弗劳德相似准则建模,模型包括工程的所有建筑物。另外,为了专门研究溢洪道,包括下游的冲刷,以及确定沿水工建筑物表面的平均和瞬时压力,建立了一个 1∶60的断面模型。

至于数值模型,考虑了一个三维断面模型(相当于半个闸墩和一扇闸门),水位条件相当于10000 a一遇洪水。从数值模型和物理模型得出了泄洪能力(闸门全开)、水面曲线以及沿溢洪道顶部和消力池的平均压力的观测结果,并进行了比较。

关于溢洪道的泄洪能力,物理模型测量的流量系数为2.016m1/2/s,而数值分析推导的流量系数为2.066 m1/2/s,比物理模型大2.5%。用常规一维公式估算的值为1.9971/2/s,比实验值小0.9%。

图 1表示 10000 a一遇设计洪水流量时物理模型和数值模型的水面曲线(水跃断面的估计相当困难)。图 2表示沿消力池的平均压力。还获得了靠近消力池侧墙的压力图。可以看出,由物理模型与数值模型得出的设计参数非常吻合,因此,在设计中可放心地采用数值模型。

图 1 圣萨尔瓦多工程的溢洪道:沿溢洪道轴线的水面曲线(数值模型和物理模型测量结果比较)

图 2 圣萨尔瓦多工程的溢洪道:数值模型和物理模型沿消力池测量的平均压力

3 皮卡乔斯坝的溢洪道

在建的皮卡乔斯坝是墨西哥锡那罗亚州正在开发的一座供水和灌溉工程的组成部分。该坝位于普雷西迪奥河上,坝高 50 m,是一座碾压混凝土坝,在平面上,坝轴线呈曲线。为下泄设计洪水,配置有 2座独立的无闸溢洪道。主溢洪道位于大坝中部,沿大坝定线的曲线堰顶长 206 m。旁侧溢洪道位于左坝肩,其堰顶轴线为直线,长 50 m。2座溢洪道的堰顶高程均为124.70 m,设计水头为 8 m,相当于溢洪道最大水头的约 83%。溢洪道泄洪能力按美国垦务局和美国陆军工程师团的标准估算(本文中称为“理论计算”)。利用这些标准,对 10000 a一遇的设计洪水(洪峰入流量为 19820 m3/s)进行演算,得到与最大泄流量 16590 m3/s相关的最高库水位为134.25 m,通过布置于高程 97 m处、半径 10 m、挑流角为 15°的挑流鼻坎向河流泄洪。

皮卡乔斯溢洪道的物理水工模型在墨西哥联邦电力委员会(C F E)的水工实验室建造与运行。按弗劳德相似准则建模,其比例为 1∶100,主要用来研究泄流条件和溢洪道对下游的冲刷影响。

溢洪道的数值模型是在进行物理模型研究之前建立的,以初步调查模型研究的水力特性。其目的是量化溢洪道的泄洪能力,识别下游泄洪不合适的水力条件(没有对下游冲刷影响进行定值评价)和斜槽水流的一般条件。

为此建立了 2个独立的数值模型。第 1个模型试图对 2座溢洪道的一般水流条件定值,第 2个模型的目的是弄清在斜槽和墙的限制条件下的水流条件。由于在整体模型中不可能(因受计算机的限制)充分离散网格来细化斜槽末端的水流条件(此处水深浅,流速高),因此使用了 2个模型,一个为整体模型,另一个为局部模型。图3和表1中给出了溢洪道泄洪能力的数值模拟、理论计算和模型实验的结果。

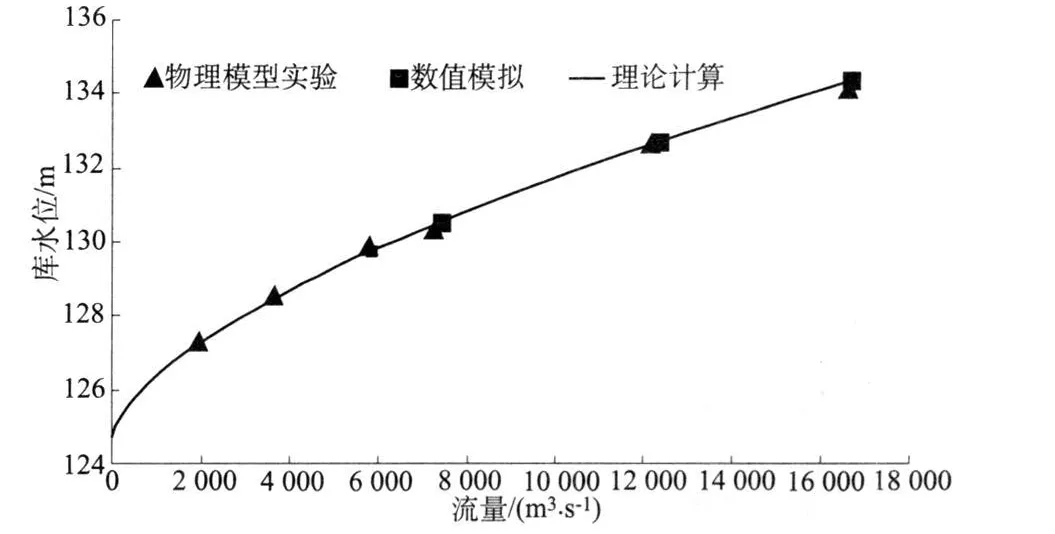
图 3 皮卡乔斯溢洪道的泄洪能力

表1 皮卡乔斯溢洪道的泄洪能力

从表 1可以看出,当库水位为129.71 m时,物理模型与理论计算之差在 4%以内。在水头大于设计水头(8 m)时,差值可能为正,反之,差值可能为负,当水头偏离设计条件时,差值的绝对值增加。这种差别可能是因网格离散化水平较低引起的,因为较大的水深包含较大的有限体积数量,从而降低了数值模型与物理模型之间的百分比误差。

从总体上看,局部和整体的数值模型得出的结论是泄洪能力符合理论计算的曲线。该结论得到了物理模型试验结果的证实。在进水口区域和沿斜槽没有发现任何不良的水流现象(如水流与边界分离或漫溢)。尽管没有考虑溢洪道下游的冲刷影响,局部模型显示,在设计条件下的射流模拟期间,没有不良影响。

在进行数值研究期间,在整体模型上模拟整个建筑物上的水流受到某些限制。在建立足够离散(详细)的三正交网格时存在困难,这种正交网格便于捕获较小水深情况下(折流装置和射流)的水流条件。在试图达到这种详细的离散水平时,单元(有限体积)的数量大大增加,受计算机的限制不能再进行计算。因为在整体模拟中离散水平不高(在某种意义上粗糙)的缘故,射流轨线的形状不能得到充分的模拟,这只有采用局部模型才有可能实现。

4 结 语

如本文所示,在水工建筑物设计中,数值模型可能是评估水力条件并确定水力参数的一个非常有用的工具。对于大型工程,数值模型可帮助优化溢洪道建筑物的几何形状和初步检查其水力条件,然后再用物理模型进行检验。对于较小的工程,物理模型在经济上不可行,因此对于简单地运用可能包含大量简化的常规理论计算来说,数值模型分析可能是一种有用的替代方法。

经研究得出下列结论:

(1)用数值模型估算得到的溢洪道泄洪能力非常接近物理模型的结果,满足大多数设计要求。

(2)数值模型便于以合理的精度研究溢洪道的水力特性,尤其是当局部模型可用多块网格构成时。例如,圣萨尔瓦多工程溢洪道消力池的平均压力非常接近于物理模型实验得到的压力。

(3)以皮卡乔斯工程为例,当建立溢洪道综合模型时,常常难以得到覆盖整个水流区域的充分离散的网格。在高流速浅水区域(例如折流装置出口和消力池进口),为了生成可靠的结果,较高的离散水平是必要的。这与流场其余部分的离散不一致,若要获得较高水平的离散,时间上不允许。甚至在使用几个单元块(多块网格)时,这一困难依然存在,因为必须保持块边界单元和尺寸的一致性。尽管有这种限制,在本文介绍的实例研究中,仍可理想地定性表示出这些区域的水流条件。