钱塘江河口细颗粒泥沙起动流速研究

曾 剑 ，陈 刚 ，熊绍隆

（1.浙江省水利河口研究院，杭州310020；2.浙江大学 建筑工程学院，杭州 310027）

细颗粒泥沙的起动流速是泥沙运动力学、河床演变学最基本的研究内容之一，也是解决河床变形、护岸工程、航道稳定等工程泥沙问题的重要参数，一直以来受到国内外学者的重视。早在1935年，Hjulstrom依据试验资料发现，当泥沙粒径D为0.2～0.3 mm时，起动流速具有极小值。此后各国学者相继进行了大量的试验研究和理论分析，从力学、随机过程等角度推导出不少起动流速公式［1-9］。以往天然泥沙起动观测资料较少，尤其是无法有效地观测细颗粒泥沙在河（海）床的起动情况，因而前人研究成果所引入的参数大部分由水槽试验来确定，水深限于0.1～0.5 m，而实际河口水深可达5～10 m，有时甚至达20 m左右，现有的泥沙起动流速公式的适用性较少得到有效地验证。

钱塘江河口是著名的强潮河口，最大潮差可达9 m，并以气势磅礴、蔚为壮观的涌潮而闻名。该河口北邻水沙丰沛的长江河口，外海来沙十分丰富，泥沙输移一潮以千万方计，相当于径流年来沙的2倍以上。河口底沙和悬沙差异较小，以细粉砂为主，中值粒径一般为0.02～0.04 mm，分选良好，由于河床滩槽组成物质经过长期往返搬运分选，缺乏粘性颗粒，抗冲能力低，易冲易淤。本文在泥沙水槽试验的基础上，根据钱塘江河口实测含沙量与流速过程资料，分析钱塘江河口泥沙的起动流速，供工程应用参考。

1 泥沙起动流速数据的获取

1.1 泥沙水槽起动试验

泥沙样本取自钱塘江河口闸口至金山河段大致均匀分布的7个断面共计9个点位的河床底沙。此外，于庆春过江隧道断面离北岸300 m和1 100 m处布设2个钻孔，自床面以下30 m范围内，每米取0.25 m长未经扰动的原状土样，按地质详勘的技术要求进行取样与密封。据统计，泥沙样本中值粒径介于0.004～0.069 mm。

泥沙起动流速试验在泥沙变坡玻璃水槽中进行，水槽长36 m，宽0.8 m，最大流量约0.35 m3/s。实验系统可通过计算机设定坡比实现无级调节，可根据模型试验要求，实现水流流量的无级调节，还可设定尾门开度，实现水槽内水位高度的无级调节。

为便于放置原型沙并模拟真实床面情况，在水槽试验段用有机玻璃垒出一块长4 m、宽0.8 m、高0.08 m梯形平台，平台上根据原型沙的不同样本形状，开挖长方形凹槽或圆形凹槽。泥沙表面用推板抹平，使泥面与凹槽墙等高，避免因水流断面变化而引起水流性质的变化，从而影响试验结果。

考虑到自循环水槽水流特点，本试验以少量动作为泥沙起动的标准。试验水深0.15～0.35 m，试验结果表明起动流速介于0.21～0.88 m/s。泥沙的起动流速与中值粒径对比关系表明，随着中值粒径的变细，起动流速将增大，即泥沙越不容易起动，这与当中值粒径D小于0.2～0.3 mm时，起动流速随粒径的减小而增加的理论分析一致。

1.2 大水深泥沙起动流速分析

依据物理概念，当水流流速小于泥沙的起动流速时，悬沙因沉降影响而落淤，此时两者的交换以悬沙转变成底沙为主，水流含沙量有所下降；随着流速的增大，底沙开始起动，此时两者的交换以底沙转变成悬沙为主，水流含沙量也随之增大。从钱塘江河口垂线平均流速与垂线平均含沙量过程线（图1）可以看出，流速与含沙量的变化有明显的对应关系。因此，对于潮汐河口，有学者认为泥沙的起动流速应取实测含沙量过程线拐点附近相应的垂线平均流速。根据上述原则，结合钱塘江河口含沙量与流速过程的实测资料，选取平均含沙量出现明显拐点、相应垂线平均流速又易于判别的典型数据，其中泥沙中值粒径选取相应时刻的悬沙中值粒径。

统计数据表明，泥沙中值粒径介于0.002 3～0.035 mm，水深范围3.0～14.5 m，两者的范围均较广，起动流速介于0.60～1.80 m/s。对比泥沙的起动流速与中值粒径、水深的关系，结果表明随着中值粒径的变小，起动流速增大，也就是说泥沙越不容易起动，随着水深的加大，泥沙的起动流速也相应增大。

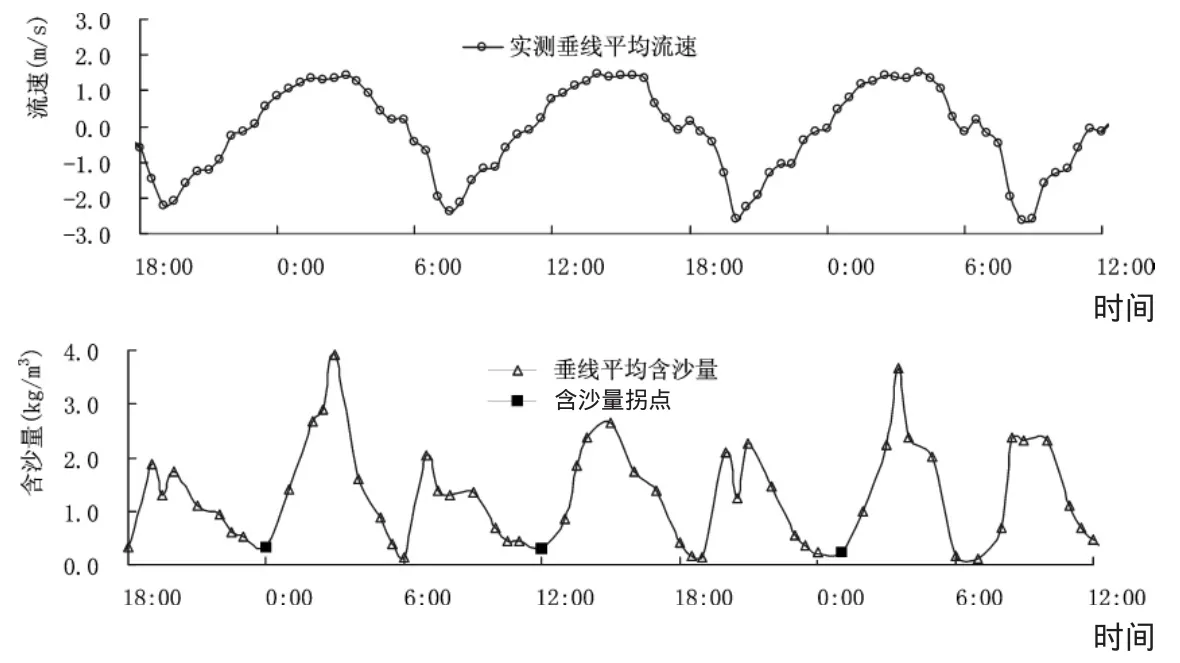
图1 钱塘江河口流速与含沙量典型过程Fig.1 Typical process of flow velocity and sediment concentration in the Qiantang Estuary

2 现有泥沙起动流速公式对比

目前天然沙起动流速的计算公式较多，对于较粗散粒体泥沙常用的起动流速公式为沙莫夫公式。当考虑细颗粒泥沙时，常用的起动公式有张瑞瑾公式［1］、窦国仁公式［2］和沙玉清公式［4］。

张瑞瑾公式

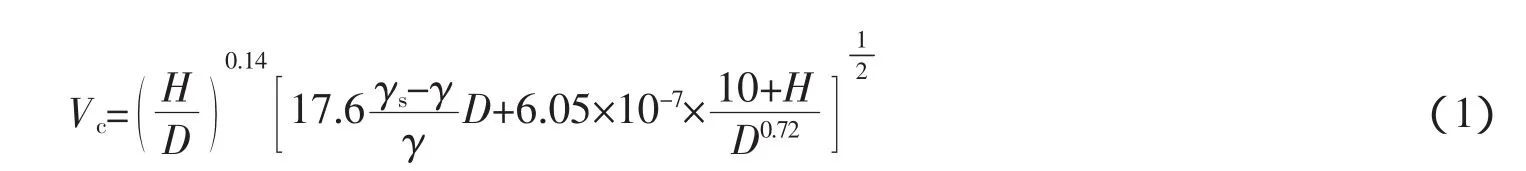
式中：H为水深；D为泥沙粒径；γs、γ分别为泥沙颗粒和水的容重。

窦国仁公式

式中：H为水深；D为泥沙粒径；γs、γ分别为泥沙颗粒和水的容重；g为重力加速度；εk为粘着力参数，取2.56×10-6m3/s2；δ为颗粒间薄膜水接触厚度，即两颗粒间薄膜水最小间距，取0.21×10-6m；Ks为糙率参数，当 D＜0.5 mm时，取0.5 mm，当 D＞0.5 mm时，Ks取D值。

沙玉清公式

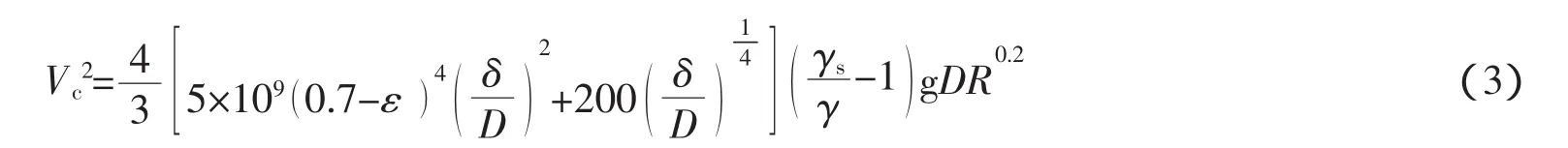
式中：ε为孔隙率；D为泥沙粒径；δ为薄膜水厚度，取10-7m；g为重力加速度；R为水力半径；γs、γ分别为泥沙颗粒和水的容重。

利用水槽试验与大水深实测资料分析的泥沙中值粒径与水深进行计算，计算结果与试验值或分析值进行比较（图2～图4）。由图2～图4可知，对于浅水深的水槽试验值，各公式均有较高的计算精度，张瑞瑾公式、窦国仁公式及沙玉清公式的计算值与试验值平均偏差分别为0.06 m/s、0.07 m/s、0.10 m/s。

对于大水深起动流速，当水深小于10 m，粒径大于0.02 mm时，张瑞瑾公式较为适合，平均偏差在0.10 m/s以内。当水深大于10 m，粒径小于0.01 mm，各公式均明显偏大，尤其是窦国仁公式偏离更大。以水深13.6 m，中值粒径0.004 mm为例，张瑞瑾公式、窦国仁公式及沙玉清公式的计算值分别达到2.72 m/s、4.88 m/s、2.52 m/s，不仅各公式相互间差异近2倍，而且与分析值也相差较大。卢金友［10］在比较各公式用于0.003 mm的长江实测资料的泥沙起动流速时，也认为公式的计算值较实测值大。

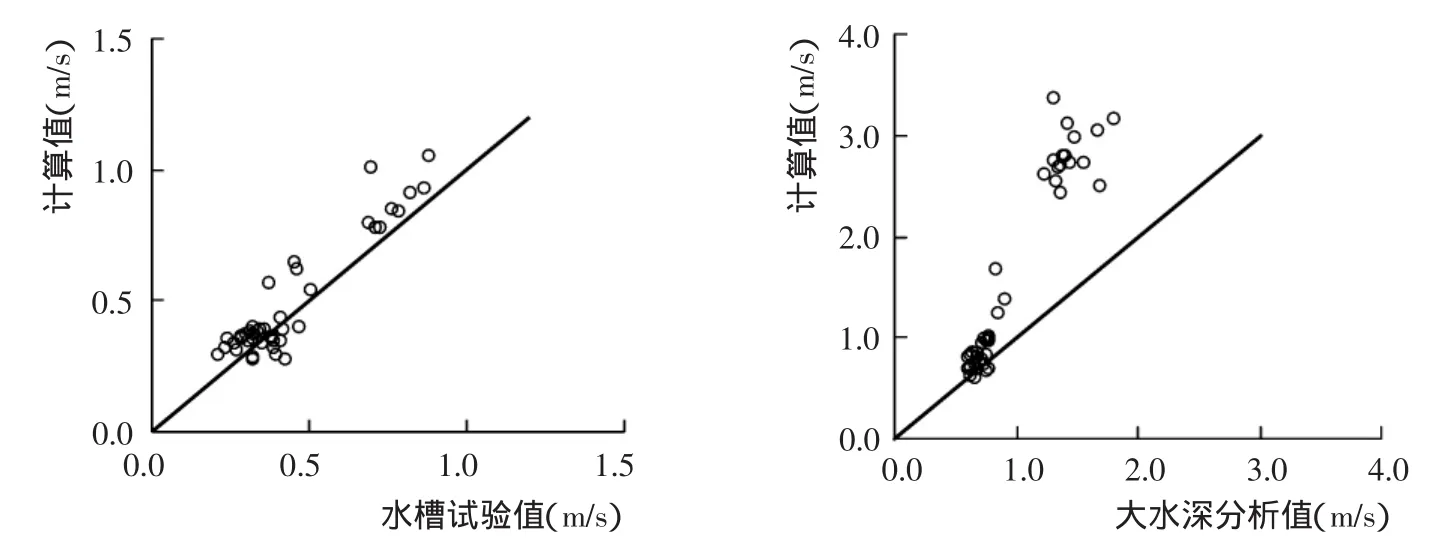
图2 张瑞瑾公式计算值与试验、分析值的比较Fig.2 Comparison of observed and calculated value based on ZHANG Rui-jin formula

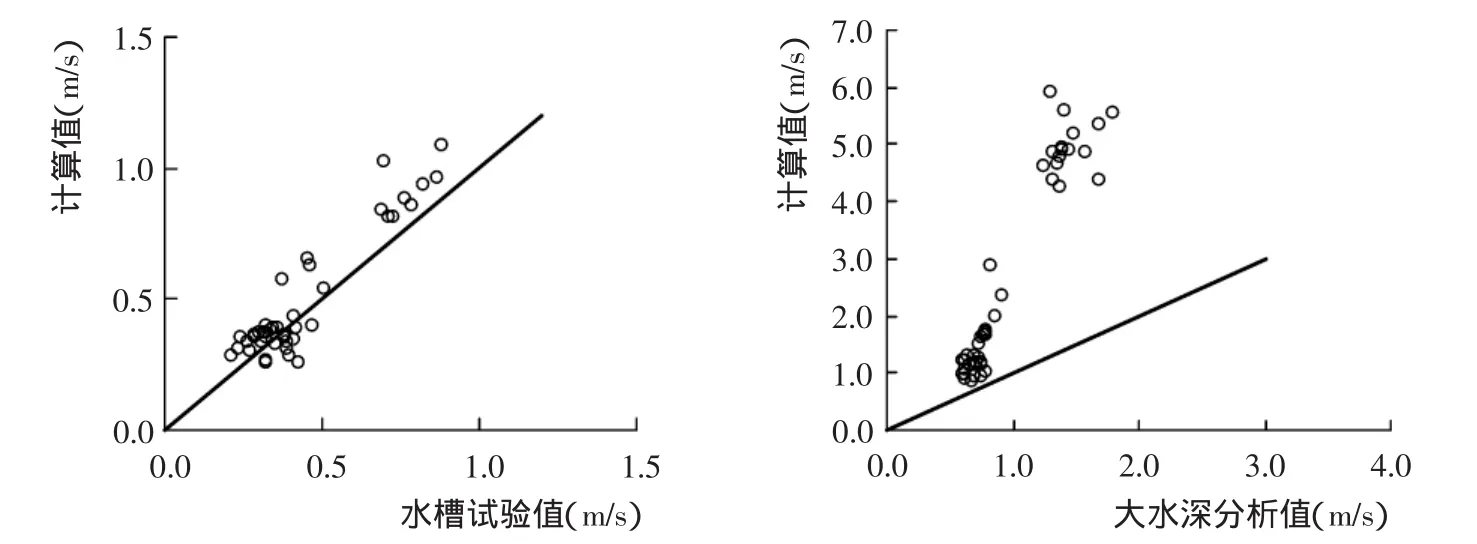
图3 窦国仁公式计算值与试验、分析值的比较Fig.3 Comparison of observed and calculated value based on DOU Guo-ren formula

图4 沙玉清公式计算值与试验、分析值的比较Fig.4 Comparison of observed and calculated value based on SHA Yu-qing formula

一般认为，河口泥沙的起动流速要明显小于相同粒径的河流泥沙，其原因可能与河口的水动力特点与泥沙特性有关：河口泥沙因径流与潮汐交互作用，上、下游往返搬运，密实程度较河流低；河口涨、落潮交替，流路随时变化，泥沙易在利于滑动或滚动的方向起动；在涨、落急时段流速梯度显著增加，尤其是强潮河口，产生了由当地加速度引起的附加应力（动力）；河口潮流流速分布随时变化，有别于河流近底层流速总是小于中、上层的情况。因此，当粒径较小且水深较大时，各公式的河口泥沙起动流速计算值远大于实际值［11］。

3 泥沙起动流速公式的修正

天然泥沙在起动过程中都要克服泥沙的重力、黏滞力、孔隙水压力等多种力的共同作用，张瑞瑾公式和窦国仁公式都是通过考虑泥沙颗粒的受力平衡而导出的，在式（1）与式（2）中，第一部分为重力作用下的起动因素，第二部分为考虑泥沙黏性薄膜与水压力作用下的附加起动因素。两者在考虑黏性薄膜与水压力时存在差异，造成两者在深水条件下的细颗粒泥沙起动流速计算值差异很大。

由于张瑞瑾公式相对适合于钱塘江河口的泥沙起动特性，为方便起见，在进行起动流速公式的修正时，采用张瑞瑾公式的形式，公式中的系数利用起动流速的试验值与分析值进行回归分析。将张瑞瑾起动流速公式改写为更一般的形式

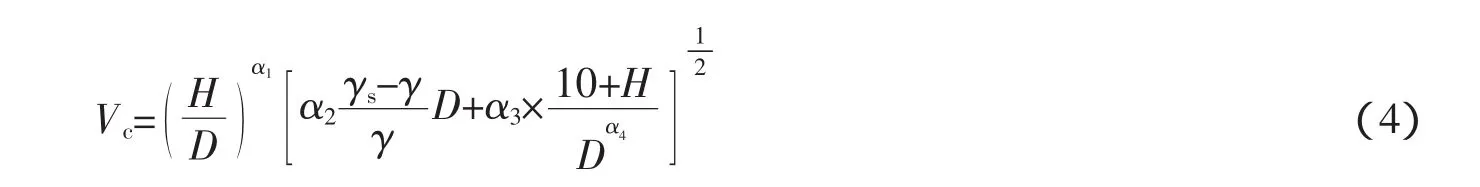
式中：α1、α2、α3与α4为待定系数。由于α1反映的是底部流速与垂线平均流速的关系，若流速沿水深分布采用近似指数公布公式，则α1可取0.14。α2反映的是重力作用对起动流速的影响，不涉及水深的因素，而且对于浅水的水槽试验值及粒径大于0.02 mm的较粗泥沙，张瑞瑾公式计算值吻合较好，因此α2可取17.6。而α3和α4两个系数则要根据现有资料进行多元回归求取。

通过对泥沙的起动流速试验值与分析值的拟合，求得起动流速公式中α3和α4值分别为0.000 031 4和0.32，图5反映了计算值与试验值或分析值的对比关系，可见两者吻合较好。因此将钱塘江河口泥沙起动流速公式修正为

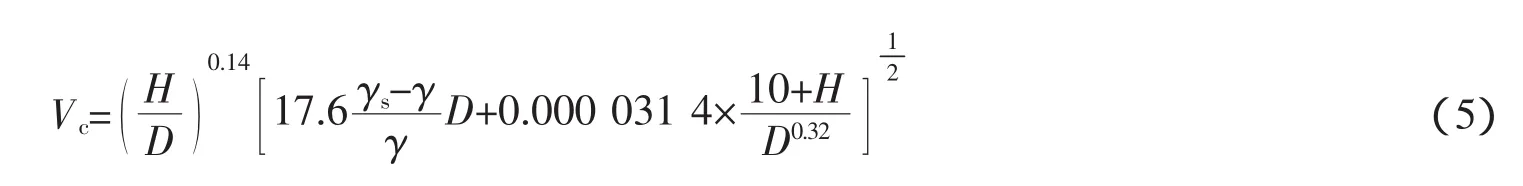
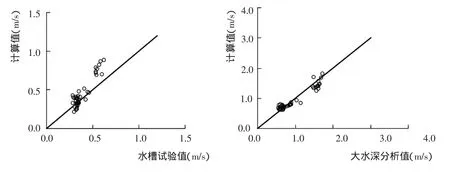
图5 修正公式计算值与试验、分析值的比较Fig.5 Comparison of observed and calculated value based on improved formula

4 结语

钱塘江河口泥沙由粉沙颗粒与少量粘土共同组成，以细颗粒泥沙为主，在强动力、高混浊以及滩槽冲淤复杂多变的河口环境中，泥沙的起动现象十分复杂。本文以实测资料为主，结合水槽试验，初步探讨了细颗粒泥沙的起动流速，认为各公式的计算值应用于钱塘江河口均偏大，据此对张瑞瑾公式进行了修正以适应钱塘江河口的水流泥沙特性。鉴于河口泥沙的复杂性，今后应进一步加强野外观测，提高含沙量测量频次，应用先进技术提高观测水平。

［1］张瑞瑾.河流泥沙动力学［M］.北京：中国水利水电出版社，1998.

［2］窦国仁.论泥沙起动流速［J］.水利学报，1960（4）：44-60.DOU G R.Incipient motion of coarse and fine sediment［J］.Journal of Hydraulic Engineering，1960（4）：44-60.

［3］窦国仁.再论泥沙起动流速［J］.泥沙研究，1999（6）：1-9.DOU G R.Incipient motion of coarse and fine sediment［J］.Journal of Sediment Research，1999（6）：1-9.

［4］沙玉清.泥沙运动学引论［M］.西安：陕西科学出版社，1996.

［5］钱宁，万兆惠.泥沙运动力学［M］.北京：科学出版社，1990.

［6］韩其为，何明民.泥沙起动规律及起动流速［M］.北京：科学出版社，1999.

［7］Yang C T.Sediment Transport：Theory and Practice［M］.New York：McGraw Hill，1996.

［8］蒋昌波，白玉川，姜乃申，等.海河口粘性淤泥起动规律研究［J］.水利学报，2001（6）：51-58.JIANG C B，BAI Y C，JIANG N S，et al.Incipient motion of cohesive silt in the Haihe River estuary［J］.Journal of Hydraulic Engineering，2001（6）：51-58.

［9］程和琴，蒋智勇，时钟.长江口南槽非均匀细颗粒泥沙起动流速的近似估算［J］.泥沙研究，2003（5）：37-40.CHENG H Q，JIANG Z Y，SHI Z.Approximate estimations of threshold velocities for non-uniform fine sediments at the South Passage of the Changjiang Estuary［J］.Journal of Sediment Research，2003（5）：37-40.

［10］卢金友.长江泥沙起动流速资料分析［J］.人民长江，1990（4）：39-45.LU J Y.Study on incipient velocity of sediment in Yangtze River［J］.Yangtze River，1990（4）：39-45.

［11］熊绍隆，胡玉棠.潮汐河口悬移质动床实物模型的理论与实践［J］.泥沙研究，1999（1）：1-6.XIONG S L，HU Y T.Theory and practice of movable bed model with suspended load for tidal estuary［J］.Journal of Sediment Research，1999（1）：1-6.