一类二阶非线性差分方程组的动力学
全卫贞
一类二阶非线性差分方程组的动力学
全卫贞
(湛江师范学院 基础教育学院,广东 湛江 524037)
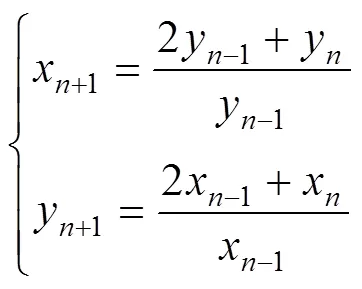
差分方程组;平衡解;素二周期解;局部渐近稳定;振荡
1 预备知识
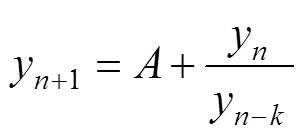
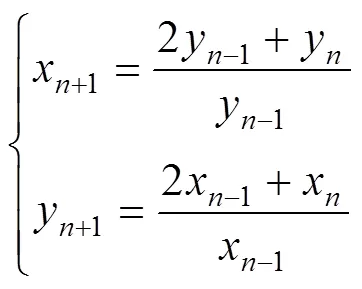
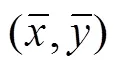
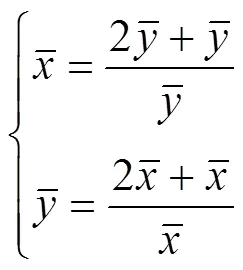
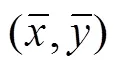
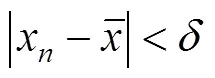
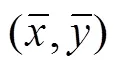

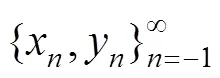
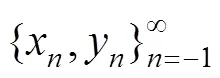
2 主要结论
定理1[5]317方程组(1)的所有解都有界,且最终介于2与4之间.


所以方程组(1)的所有解都有界,且最终介于2与4之间.
定理2 方程组(1)无素二周期解.
证明 参考文献[6]8的反证法,假设方程组(1)有素二周期解
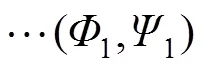

整理得:
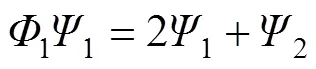
所以有:


故方程组(1)无素二周期解.
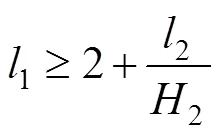



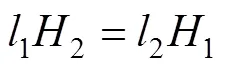
2.4 临床妊娠结局对比 随访至今,试验组的临床妊娠率与着床率明显低于对照组,而自然流产率高于对照组,两组比较差异有统计学意义(P<0.05),见表2。

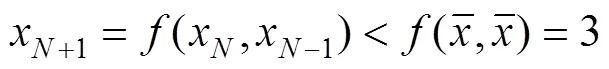
所以
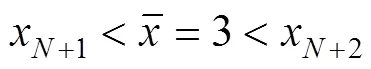


[4] KULENOVIC M R S, LADAS G. Dynamics of second order rational difference equations [M]. Chapman & Hall: CRC, 2002.
[5] 王丽丽. 差分系统正解的全局渐近性[J]. 太原科技大学学报,2008, 29(4): 317-318.
[6] 袁晓红,晏兴学,苏有慧. 一类有理差分方程的周期性和振动性[J]. 河西学院学报,2009, 25(2): 7-13.
[7] 马学敏. 一类高阶差分方程的定性研究[J]. 株洲师范高等专科学校学报,2007, 12(2): 28-30.
[责任编辑:熊玉涛]
The Dynamics for a Class of Second Order Nonlinear Difference Equations
QUANWei-zhen

system of difference equations; equilibrium point; solution of prime period two; locally asymptotic stability; oscillation
1006-7302(2010)03-0004-10
O175.7
A
2010-03-07
广东省自然科学基金资助项目(07301595)
全卫贞(1980—),女,广东湛江人,讲师,在职硕士生,研究方向:差分方程与动力系统,E-mail: Quan801015@126.com.

