冬小麦水肥生产函数最小二乘法回归建模及分析

曹永强,刘 琳,姜 莉,张伟娜

(1.辽宁师范大学城市与环境学院,辽宁大连 116029;2.农业部农业环境与气候变化重点开放实验室,北京 100081;3.中国科学院水利部水土保持研究所黄土高原土壤侵蚀与旱地农业国家重点实验室,陕西杨凌 712100)

关于作物的水肥与产量关系研究由来已久,但真正的量化关系研究特别是水肥协调关系方面的量化研究则是进入19世纪以后[1]。化肥的大量施用,不仅带来农业生产成本的增加,还对土壤及地下水造成污染。因此,如何提高作物对水肥的利用效率、减少化肥污染、提高农业生产效益,是目前及今后长时间内有效地进行农业水肥管理的一个重要方面。解决这一问题的基础是对水-肥-作物产量关系(作物水肥生产函数)进行研究[2]。人们从不同的角度入手探讨水分与作物产量的关系,建立了多种作物水分生产函数模型。归纳起来,这些模型可分为2大类:一类是以作物耗水(作物蒸腾量或腾发量)为变量,寻找不同生育阶段不同程度的水分亏缺与产量的关系;一类是建立作物生产过程不同农田水分状况与干物质累计量之间的关系[3]。Ozsabuncuoglu[4]通过试验建立了冬小麦的全生育期产量模型,该模型为多元线性模型,它考虑了生长期和成熟期的降雨、温度和施肥;徐学选等[5]在黄土丘陵区(固原)研究了春麦产量与降水和土壤供水的关系,定量描述了底墒和生育期降水与产量的关系。笔者在分析北京市水利科学研究所永乐店试验数据的过程中,选择最小二乘回归建立了具有较高精度和预测能力的冬小麦水肥生产函数模型,并对水肥耦合效应进行了分析。

1 试验和数据

1999～2000年在北京市水利科学研究所永乐店试验站的24个田间小区进行了冬小麦水肥二因子非充分灌溉试验。试验站位于北京市通县永乐店镇(地理位置116.8°E,39.7°N),试验区土质为砂壤土,土壤密度为1.4 t/m3,田间持水量为36.5%。化肥的施用主要是氮肥,为了进行对照,试验分为不施肥、少施肥、中施肥和高施肥4种情况。各小区的水肥投入量和产量见表1。用ET表示由田间水量平衡分析求得的作物在整个生育期间的腾发量(腾发量=降雨量+灌溉量-土壤根系层含水的增加量),有了腾发量(或灌溉量)和施肥量,就可以建立作物全生育期的腾发量、施肥量与最终产量的函数模型。这种模型适用于缺少大量试验数据区域的作物产量与水肥关系的模拟,尤其是在干旱地区应用起来很方便。

表1 1999～2000年水肥试验数据

2 最小二乘回归的基本原理

普通最小二乘法(ordinary least square,简称OLS),是应用最多的参数估计方法。最小二乘估计是一种方差最小的估计,有很强的优良性。它通过最小化误差的平方和找到一组数据的最佳函数匹配,求得一些未知的真值。

在实际问题中,与某随机变量y有关系的变量往往有多个,而且它们之间的关系是非线性的。研究随机变量y与一般变量x1,x2,…,xt之间的相关关系问题便是多元非线性回归问题。为了寻找y与一般变量x1,x2,…,xt之间的相关关系,首先必须收集n组独立观测值[6]xi1,xi2,…,xit,yi(i=1,2,…,n)。

对n个有限样本的多元回归模型:

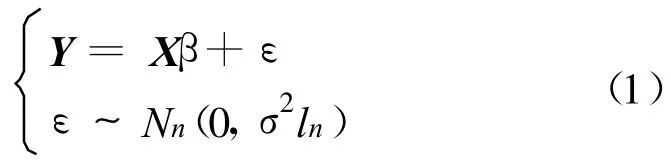
其中

参数的最小二乘估计:令

则各 βi的最小二乘估计应该满足

由于 Q(β0,β1,…,βt(t+3)/2)是 β0,β1,…,βt(t+3)/2的非负二次式,且关于 β0,β1,…,βt(t+3)/2均可微,因而根据微积分原理,,,…,是下列方程组的解:

通过整理可将其用矩阵表示为

当(X′X)-1存在时,其最小估计为

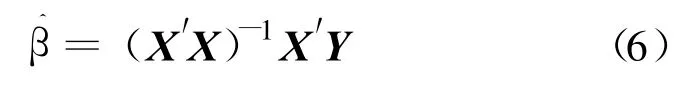
3 最小二乘回归建模

关于冬小麦产量与农田耗水量的关系众说不一,有直线、抛物线及对数型等关系,多数研究者采用抛物线(二次多项式)来描述两者的关系:当耗水量超过需水量时,产量不但不增加,而且有可能降低。然而由于影响产量的因子不止是水分,肥料也是影响作物产量的重要因子,不妨将冬小麦产量与水肥2个因子的关系用二元二次多项式进行拟合。

设ET为 x1,化肥投入量为 x2,产量为y,通过多元回归,可以建立包含交叉项的水肥生产函数模型:

利用最小二乘回归原理,借助SPSS软件可以求得1999～2000年的水肥生产函数模型各项系数如下:β0=-78.159,β1=1.388,β2=2.831,β3=0.000737,β4=-0.023 5,β5=0.000 28。复相关检验:R2=0.866 3,R=0.931;显著性检验:F=23.65＞F0.95(5,14)=3.66,可认为上述回归方程(式(7))是显著的。

产量模型计算值与实测值的拟合结果如图1所示。另假设化肥量为 150 kg/hm2,200 mm＜ET＜320mm的水肥组合系列,采用1999～2000年的水肥生产函数模型系数计算相应的产量。从表2可知计算结果较接近实际值,说明最小二乘回归可求得正确的水肥生产函数模型。

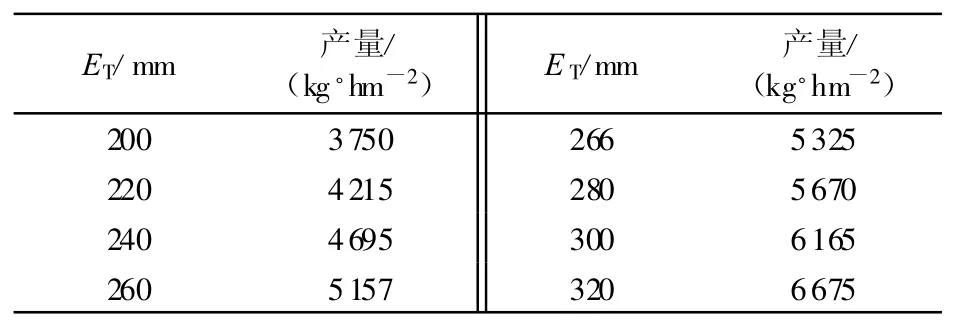
表2 最小二乘回归模型模拟得到的冬小麦产量

图1 最小二乘回归产量拟合

多元回归模型的使用有一个前提,就是自变量之间不能存在严重的多重相关性。当X中的变量高度相关时,行列式几乎接近于零(条件数趋于无穷大),求X′X的逆阵会含有严重的舍入误差,因此回归系数容易受较大舍入误差的影响,从而增加估计值的抽样变异性。可以用简单相关系数粗略地分析自变量之间的多重相关性。表3列出了1999～2000年水肥生产函数回归模型自变量之间的简单相关系数。从表3中可知,回归变量之间的相关系数比较小,所以认为回归变量之间不存在多重相关性。

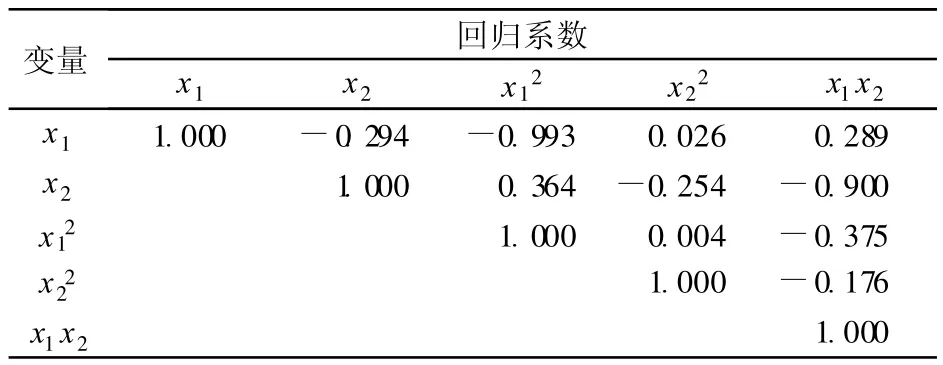
表3 回归变量之间的简单相关系数

最小二乘回归的具体计算通过SPSS软件实现,具体参见文献[7]。

4 对最小二乘回归模型的分析和讨论

由最小二乘法求得的水肥生产函数可以拟合1999～2000年冬小麦实测产量与计算产量。从图1来看,拟合结果具有较高的精度。但由于试验数据是小样本容量,还不足以据此判断所建立回归模型的正确性、稳健性及预测能力。为了进行判断,可以假设代表各个试验处理水平的数据,利用模型模拟,根据产量的模拟值来验证模型是否合理[8]。图2反映了化肥投入量不同时的ET和产量关系。从图2中可以断定最小二乘回归得到的水肥生产函数模型是稳定可靠的,可以据此分析水肥耦合效应[9]。

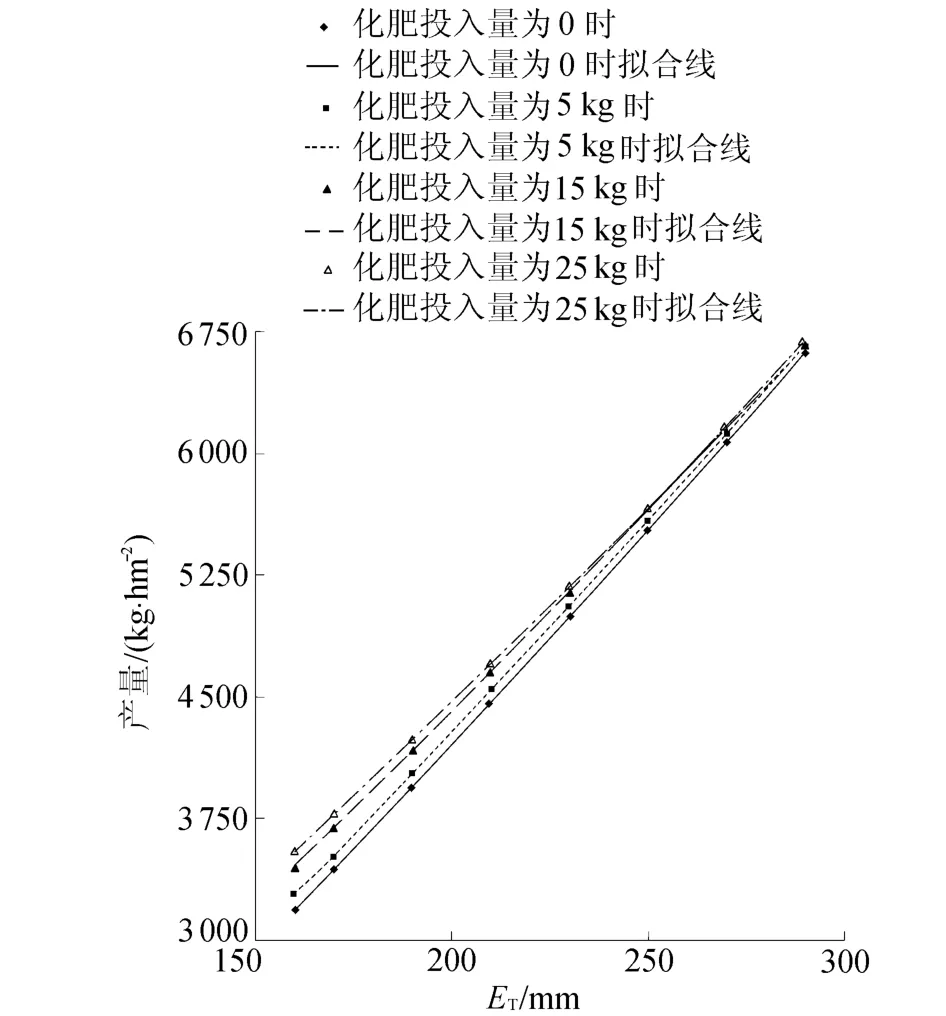
图2 最小二乘回归模型模拟的1999～2000年冬小麦产量

由式(7)和表2对1999～2000年的水肥生产函数求一阶偏导数:根据式(8)、式(9)可以进行如下分析。

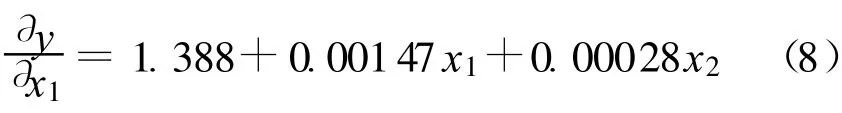
a.水肥的单因子效应。水肥生产函数一阶偏导数的常数项都大于零,且一次项系数远小于常数项,所以水肥投入量处于一定区域时两者都有明显的增产效应[10]。由式(8)和式(9)可知,当 ET不变时,随着化肥投入量的增加,边际效应递减,甚至成为负效应。例如,若ET固定为250mm,当化肥投入量由45kg/hm2增加到375kg/hm2时,化肥投入量的边际效应由2.66下降到1.73。值的大小表示了ET的边际效应。在化肥投入量一定的情况下,随着ET的增加而增加。但由于一次项系数很小,所以可以认为基本保持不变。也就是说,在化肥投入量一定的情况下,产量与 ET的关系可以近似为直线关系。

b.水肥耦合效应。水肥生产函数的交叉项化肥的系数为正表明,水肥耦合效应表现为对产量的协同作用,该作用能促进产量的提高。增加化肥投入量有利于提高作物水分利用效率,反之亦然。

5 结 语

用多元非线性回归方法分析水分、肥料对冬小麦产量的耦合影响,结果表明,只有当水分和肥料合理搭配时才能充分发挥它们的作用。多元回归分析时,最小二乘回归可正确地估计模型参数。利用该方法建立了北京市水利科学研究所永乐店灌溉试验站1999～2000年的水肥生产函数回归模型。

模型的模拟结果表明该模型参数估计合理。对模型的分析表明,ET和化肥2个因素都具有明显的增产效应。在化肥投入量不变的情况下,作物的水分利用效率随着耗水量的增加而有所增加;在作物耗水量保持不变的情况下,作物肥料利用效率随着肥料投入量的增加而下降。在一定范围内,增加化肥投入量能够提高作物产量,但在一定范围之外增加化肥投入会引起作物减产。

[1]翟丙年,李生秀.冬小麦产量的水肥耦合模型[J].中国工程科学,2002,4(9):69-74.

[2]张凤翔,周明耀等,郭凯泉.水肥耦合对冬小麦生长和产量的影响[J].水利与建筑工程学报,2005(2):24-26.

[3]沈荣开,张瑜芳,黄冠华.作物水分生产函数与农田非充分灌溉研究述评[J].水科学进展,1995,6(3):249.

[4]OZSABUNCUOGLU I H.Production functions for wheat:a case study of Southwestern Anatolian Project(SAP)Region[J].Agricultural Economics,1998(18):75-87.

[5]徐学选,穆兴民.小麦水肥产量效应研究进展[J].干旱地区农业研究,1999,17(3):6-12.

[6]周纪芗.回归分析[M].上海:华东师范大学出版社,1993:33-50.

[7]薛薇.SPSS统计分析方法及应用[M].北京:电子工业出版社,2004.

[8]康绍忠,胡笑涛,蔡焕杰,等.现代农业与生态节水的理论创新及研究重点[J].水利学报,2004(12):1-7.

[9]胡庆芳,尚松浩,温守光.潇河冬小麦水肥生产函数偏最小二乘回归建模及分析[J].节水灌溉,2006(1):1-4.

[10]薛亮.夏玉米分根交替灌溉施肥的水肥耦合效应研究[D].杨凌:西北农林科技大学,2008.