基于三维J积分的裂缝稳定性仿真计算
李子阳,李 季,向 衍
(1.南京水利科学研究院,江苏南京 210029;2.水利部大坝安全管理中心,江苏南京 210029;3.黄河上游水电开发有限责任公司,青海西宁 810008)
在水利工程中,裂缝是影响建筑物安全与正常运行的不利因素之一。但由于裂缝物理特性的非线性以及尖端处应力应变的奇异性,使得有限元模拟计算困难,往往难以得出准确结果。目前进行裂缝稳定性分析主要有4种判据:在工程断裂安全分析方面,由于缝端应力强度因子KⅠ可以采用位移直接法计算,分析手续简单,应用最为广泛[1-4]。但KⅠ是基于线弹性的公式,对弹塑性材料存在塑性区修正的问题,为满足精度要求,分析中对缝端单元尺寸及选用外推节点有很多限制[5-6]。即便如此,采用靠近缝端的节点位移和采用远离缝端的节点位移进行外推得到的KⅠ仍常存在较大差异,难以进行规范化比较。而J积分由于是从能量角度对含裂缝物体的应力应变场进行分析,可以避开裂缝尖端应力应变求解的困难,已成为研究弹塑性断裂力学的主流。但J积分的研究分析多限于平面问题,三维J积分的理论虽然已经比较成熟,但由于还存在积分路线确定及J积分有限元计算等定量实现上的技术问题,在水利工程中的应用还未能开展。据此,本文就三维J积分并入有限元计算程序中的计算处理方法进行讨论,以提供一些三维J积分应用的实现技术。
1 三维J积分定义
为了避开求解裂缝前缘塑性区应力应变场时数学上的困难,Rice[7]从能量守恒出发,利用格林公式分析了平面裂缝尖端区域应力应变场的强度,首次将J积分应用于断裂力学。在实践中,为解决J积分对处理空间含裂纹问题存在的困难,陈国栋等[8]利用势能原理和格林定理导出了三维J积分表达式,并用高斯公式证明在满足不计体力、小应变以及单调加载等条件下,三维J积分值与积分曲面无关。

三维J积分可定义为以下曲面的积分:)式中:Σ为裂缝下表面到上表面任一包围缝端的积分曲面;W为曲面上任一点的形变能密度函数,分别为应力和应变),若采用线弹性本构关系,则;n为 Σ上的向外单位法线;T为作用在Σ上沿外法线方向的张力矢量;b为缝端位移方向(表明其扩展方向)的单位法线矢量;u为Σ上的位移矢量。
为解决分析及评判的一致性问题,宫本博[9]进一步提出了单位长度J积分的计算形式(取裂缝扩展方向为x方向,如图1所示):式中:B为计算裂缝长度;ui为i方向上的位移;i=1,2,3。


图1 三维J积分有限元积分曲面
2 三维J积分有限元计算的程序实现
J积分并入有限元计算主要存在积分路径的搜索及依据有限元结果的积分实现等技术问题,对此作以下讨论。
2.1 积分回路的拓扑搜索
虽然理论上J积分对回路的选择没有要求,但在实际的有限元模拟计算中考虑单元的离散性及计算的易实现性,实际的回路选择都是以已有的线面为参考。积分路径可以直接定义,但需要一定的计算经验,显然不利于程序自动化的实现。为此,根据有限元网格中点面之间连接的拓扑关系,采用拓扑搜索自动定义积分路线。
考虑单元的划分及计算方便,三维J积分曲面一般选择成由2个侧面S2和S3与1个沿裂缝长度方向的主面S1组成(如图1)。由于两侧面积分对J积分值贡献很小,基本不超过1%[9],故忽略不计,只对主积分面 S1进行积分路径寻找及曲面积分,以简化J积分的计算。
将积分曲面寻找转化成面上各积分回路节点寻找(然后对应节点相连构成面信息)的平面拓扑搜索问题,则按照拓扑搜索的概念,积分回路的定义就是根据缝端区域单元或节点间的拓扑关系,首先拓扑发现路径所在的区域,然后通过建立节点间的邻接矩阵拓扑搜索约束化外回路。积分路径拓扑搜索的实现步骤包括收集拓扑信息、研究回路区域、生成节点邻接矩阵和回路的自动搜索。
2.1.1收集拓扑信息
根据有限元程序获得的缝端区域单元及节点信息,收集并设定如下所需拓扑信息:①缝端节点及各积分回路起始、结束节点编号;②裂缝周围积分区域的单元面拓扑信息,包括单元面编号及单元面节点组成等,并以单元面信息为基础,利用对象选择集函数得到边线段信息,由此确定面中节点的拓扑连接关系。
2.1.2确定回路区域
寻找包含上一积分回路节点(缝端节点作为初始积分回路)且不为上一回路区域(积分回路所包围的区域)的所有单元面,删除面法向与缝长度方向一致的单元面,由此得到第i个回路区间,将该区间所有节点中上一回路区域的节点删去即得到构成该积分回路的所有节点。
2.1.3生成节点邻接矩阵
在拓扑图中,点与点之间的连接关系可以用邻接矩阵来描述。即把N个点的拓扑图表示为N×N个元素的对称矩阵,行与列的元素都代表点的编号,如果拓扑图的i点与j点之间有边连接的话,其邻接矩阵A中aij元素的值取为1;否则为0。
确定回路节点集的邻接矩阵步骤如下:①邻接矩阵A的行、列数均为节点数m;②把矩阵A的所有元素值aij置为零;③对照回路区间线段表,若节点 ai与aj相连的话,则在第 i行第j列赋值为1,依次填充矩阵。由此确定的邻接矩阵为对称矩阵。邻接矩阵建立了节点间的拓扑关系,为实现回路的拓扑连接搜索提供了数据结构上的支持。
2.1.4回路的自动搜索
利用邻接矩阵自动搜索回路。设回路节点为m个,为讨论方便,用ni,k表示某一行的列号,表示ni,k的邻接标号,即

整个搜索过程由第1行开始,依次判断邻接矩阵大于0的元素作为起点。为讨论任意性,设[i1,i2]处的值 ai1,i2大于0,记录 i1为第 1点,i2为第2点,然后转到[i1,i2]的对称元素[i2,i1];在第 i2行搜索ai2,i1的邻接标号及再邻接标号,直至找到ai2,i3>0,把列号 i3记录为第3点,然后再在i3行搜索第4点……这样经过若干次搜索之后,搜索到所给的结束点时即可结束此次搜索。搜索的具体顺序可以表示成式(4)的形式。

由上述步骤,使用网格拓扑搜索就可以自动定义多个不断增加尺寸的回路区域,而这些区域的边界节点拓扑连接即成为积分回路。其中,第1回路区域由所有连接到裂纹尖端单元的节点构成,下一区域在前一区域的基础上加上与前一区域节点相连的所有单元节点。对于每个缝端节点分别确定积分区域,各区域呈辐射状增长,对于规则网格,相当于创建了一个垂直于裂纹前缘的节点盘。完成所有缝端节点积分路径的寻找,即可根据节点对应关系确定积分曲面。为了搜索及计算方便,一般要求裂缝前沿网格应由退化的规则六面体单元组成,由此三维裂缝拓扑搜索确定的积分回路如图2所示。
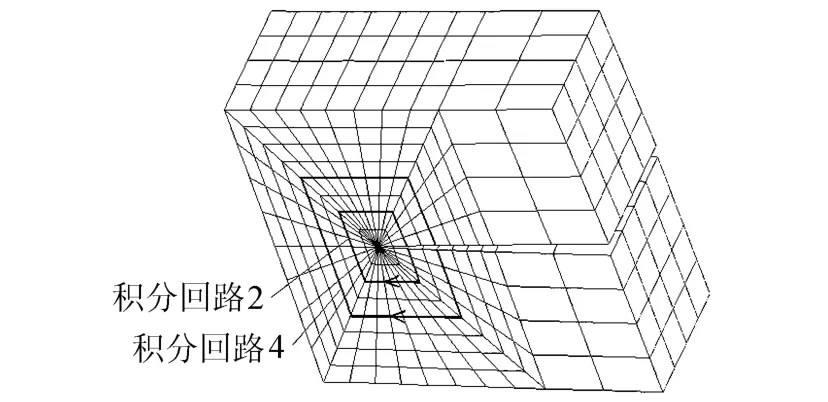
图2 三维裂缝拓扑搜索J积分路线
2.2 积分的计算
在式(2)中,令
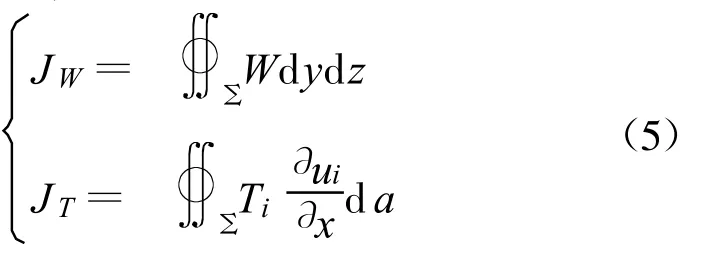
在有限元中,积分曲面 Σ被分割为一系列的单元面。如果可以求出 Σ上每个单元面的JW与JT,那么将所有的单元面结果相加,即可求得 Σ上的J。据此,将J的计算考虑如下:对于单个单元面,采用线弹性本构关系,则式中:ne为该单元面外法线方向矢量。
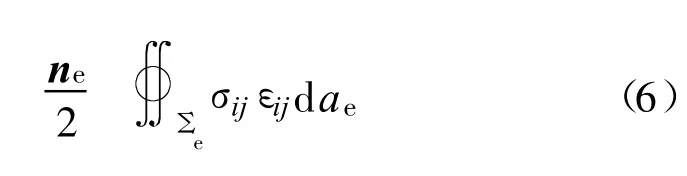
对此,如果能求得单元面上的应力、应变函数及面边线的空间方程,则可进行精确计算。但有限元分析往往只给出节点的计算结果,函数形式还需要利用插值手段构建;另一方面需要积分的单元面较多而且形状可能很不规则,积分边界的确定比较麻烦。
为了避开积分运算并获得较高的精度,仍然采用有限元离散的思想,即将单元面各自边的中点连接拆分成4个区域(图3),对每个区域继续划分还可分解成16个、64个等。对于每个小的区域,可近似认为应力、应变值保持不变(取四节点平均值)。如此有
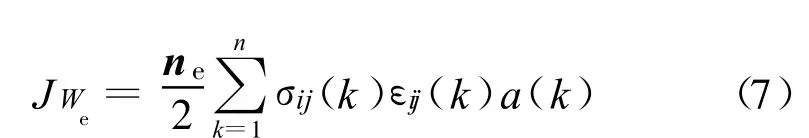
式中:σij(k),εij(k)分别为第 k个区域的应力、应变值;a(k)为第k个区域的面积。
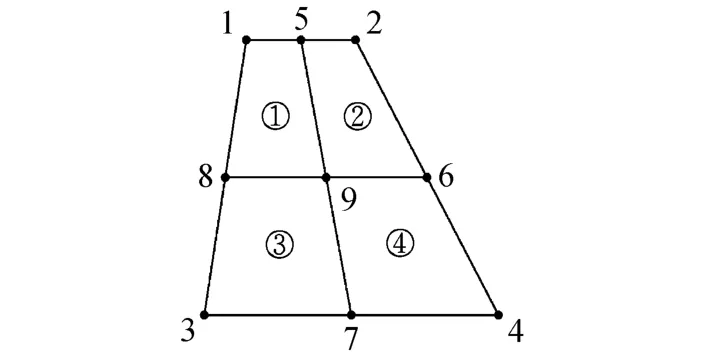
图3 积分剖分处理示意图
对于JT,设n1,n2,n3为面元da外法线n的方向余弦,由力的平衡条件有

可求得


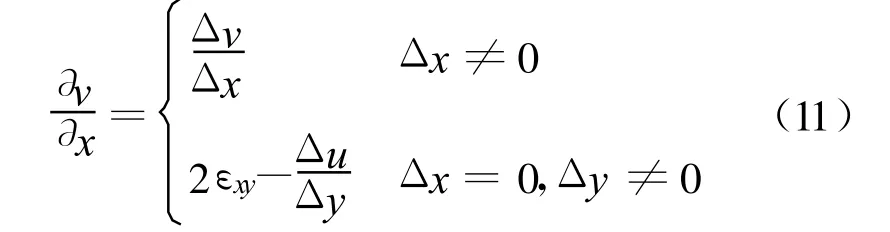

同样地,把每个单元面划分成多个积分区域,有
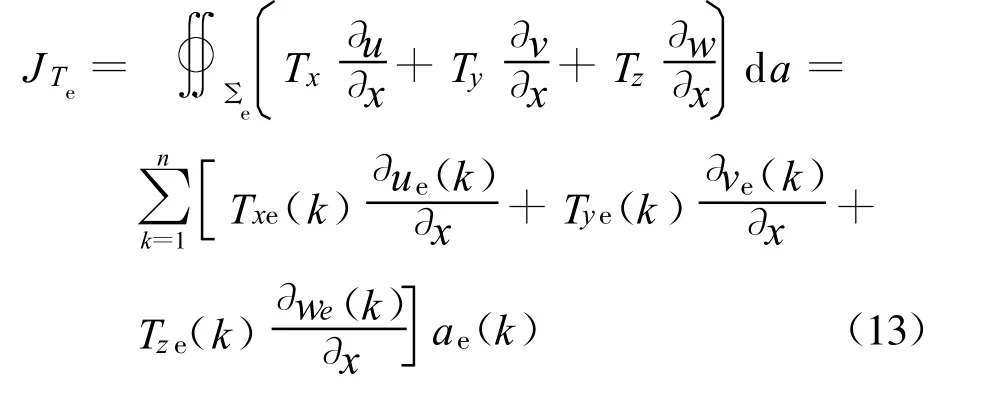
由此得

3 实例分析
某重力拱坝坝高178 m,水库正常高水位为2600m。坝址区属大陆性气候,全年冷期长,气温变差大。自运行以来,在坝体下游面出现130多条裂缝,且以水平裂缝居多,其中30多条水平裂缝贯穿坝段下游面。裂缝成因分析表明裂缝主要由低温拉应力引起,为Ⅰ型裂缝,比较危险。为此,选取拱冠梁2560.00m高程处水平裂缝作为典型裂缝,应用J积分法对其进行稳定性分析,并与应力强度因子法所得结果进行对比。由于没有成熟的模拟裂缝自动扩展的有限元应用模型,对裂缝开裂深度进行假定(分别假定为1.0m,2.0m,3.0m,4.0m等),分别分析其稳定性。
对大坝建立三维有限元分析整体模型,见图4。其中水平裂缝的缝端局部细化如图5所示(开裂深度为2.0m,其余不同开裂深度的模型类似)。裂缝区(填充区所包含区域)采用退化六面体单元,缝端加密单元尺寸0.125m左右,沿裂缝开裂方向单元尺寸定义为1m,简化了模拟不同开裂深度时模型的重新划分(只需将裂缝区沿开裂方向平移),裂缝区与整体采用Glub技术接触连接。计算时采用反演和设计参数,考虑材料非线性,采用Drucker-Prager屈服准则。温度场计算以水温、气温和坝内温度计测值近似作为边界约束条件,封拱温度场取为7℃。由于裂缝主要是由低温引起,为Ⅰ类拉开型,裂缝及横缝均采用Contact单元模拟其接触及受拉张开性态[10]。
模型计算中选取典型荷载工况为:水压、自重、低温等单项荷载工况以及水压+自重+低温组合工况。经对各种工况下总体有限元模型分析,结果表明水平裂缝在“2590m水位+低温+坝体自重”工况下梁向拉应力最大,对稳定最不利,因此,分析此最不利荷载工况下裂缝的稳定性。
裂缝计算所得不同开裂深度时的JⅠ积分值与缝端应力强度因子KⅠ外推值列于表1。由表1可以看出:在小范围屈服及合理选取外推节点计算KⅠ的情况下,JⅠ与KⅠ具有类似的计算结果;当水平裂缝开裂深度为4.0m时,KⅠ<KⅠC,且JⅠ<JⅠC,说明此时裂缝达到稳定状态。

表1 缝端应力强度因子KⅠ及 JⅠ积分值
图6与图7分别列出了假设开裂深度为2.0m时采用距缝端不同距离节点有限元结果计算出的KⅠ值及不同积分路径的JⅠ积分值,可以看出:KⅠ有很强的距离依赖性,选取不同的节点值外推,其结果可能差别较大;而JⅠ积分值的路径依赖性很小,基本一致。故JⅠ积分作为裂缝稳定性与否的判断依据更有可比性及参考性。

图4 大坝三维有限元模型

图5 裂缝细化有限元分析模型

图6 距缝端不同距离应力强度因子计算值

图7 不同积分路径JⅠ积分计算值
4 小 结
鉴于J积分从能量角度对含裂缝物体的应力应变场进行分析,可以避开裂纹尖端应力应变求解的困难,将三维J积分计算并入有限元计算程序中,并对计算实现的技术方法进行了讨论,包括通过建立节点间的邻接矩阵实现积分回路拓扑搜索以及积分计算的离散方法等。实例分析表明其与合理选取外推节点计算的KⅠ具有类似的计算结果。但J积分对单元尺寸大小要求不高,路径依赖性也很小,作为裂缝稳定性与否的判断依据更有可比性及参考性,可有效提高对裂缝的分析水平。
[1]黄耀英,吴中如,顾冲时,等.缝端应力强度因子对网格尺寸的敏感性分析[J].岩石力学与工程学报,2007,26(S2):41-47.
[2]李先明,秦忠国.闸墩混凝土表面温度裂缝稳定性断裂力学分析[J].河海大学学报:自然科学版,2007,35(4):422-424.
[3]李子阳,王建,金永强.大坝水平裂缝稳定性分析[J].水力发电,2007,33(7):36-41.
[4]李同春,刘晓青,吕泰仁,等.柘溪水电站多联体坝裂缝稳定三维随机分析[J].河海大学学报:自然科学版,1997,25(增刊):86-89.
[5]朱伯芳.有限单元法原理与应用[M].北京:中国水利水电出版社,1998.
[6]于骁中,张彦秋,曹建国,等.混凝土复合型(Ⅰ、Ⅱ型)裂纹断裂准则的计算和试验研究[J].水利学报,1982(6):27-37.
[7]RICE J R.A path independent integral and the approximate analysis of strain concentration by notches and crack[J].Appl Mech,1968,35:379-386.
[8]陈国栋,吕运冰,汪冬生.空间体J积分表达式及其守恒性[J].武汉理工大学学报:交通科学与工程版,2007,31(1):130-132.
[9]宫本博.弹塑性断裂力学[M].杨秉宪,王幼复,编译.太原:山西人民出版社,1983.
[10]李子阳,谷艳昌,张磊.基于Marc的高拱坝蓄水期变形分析[J].水利水电科技进展,2008,28(4):15-19.
[11]沈长松,陆绍俊,林益才.混凝土重力拱坝下游面裂缝断裂稳定性初析[J].河海大学学报:自然科学版,1995,23(1):22-29.
[12]KANNINEN M V F,POPELAR C H.高等断裂力学[M].洪其麟,郑光华,郑祺选,等,译.北京:北京航空学院出版社,1987

