Zakharov方程组的一些新精确解
杨立波,卢殿臣
(1.淮阴工学院 数理学院,江苏 淮安 223003;2.江苏大学 非线性科学研究中心,江苏 镇江 212013)
0 引言
求解非线性波动方程的精确解在非线性问题的研究中占有重要的地位,直接寻找非线性方程的精确解,一直是数学家和物理学家的重要研究课题。近几年来,研究人员对求解非线性发展方程的精确解提出了许多方法,如齐次平衡法、双曲函数法、F-展开法、反散射法、投射的Riccati方程法等,利用这些方法求得了非线性发展方程的许多丰富的精确解。为了进一步求得非线性波动方程的广义上的周期解,有人提出了Jacobi椭圆函数展开法,由于这种方法可借助于计算机代数系统得以实现,因此得到了广泛的推广和应用。然而,寻找新形式的精确解仍是一件非常有意义的工作。
本文在投射的Riccati方程法和Jacobi椭圆函数展开法的基础上,构造了4种新的Jacobi椭圆函数解,并利用该方法求出了Zakhaorv方程组的一系列新的精确解,包括周期解和孤波解,并对解的结构做了分析。
1 扩展的Jacobi椭圆函数展开法
对于给定的非线性发展方程,其一般形式可写为:

式中的 F 是关于变元 u,ut,ux,utt,txt,uxx,… 的多项式。
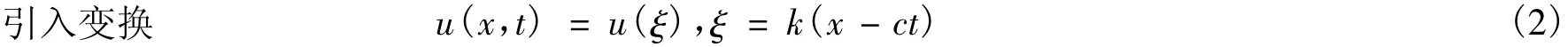
其中k和c是非零的待定常数。
将(2)式代入(1)式,得到关于u(ξ)的常微分方程

设方程式(3)具有如下形式的行波解
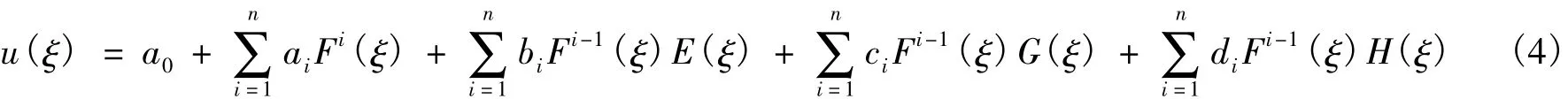
其中 a0,ai,bi,ci,di(i=1,2,…,n) 是待定常数,ξ= ξ(x,t) 是关于 x,t的函数,正整数 n 的值通过平衡方程(3)中的非线性项和最高阶导数项来确定。F(ξ),E(ξ),G(ξ),H(ξ)的选取本着计算简单的原则,可从e,f,g,h 中任意选择,其中
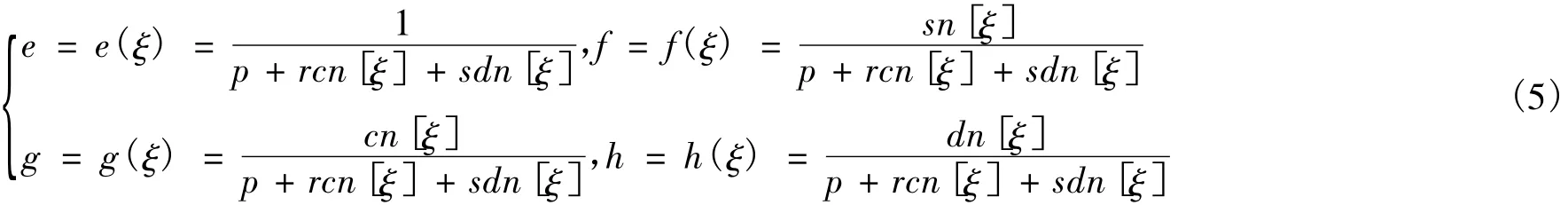
其中 p,r,s是任意常数,e,f,gh 这 4 个函数满足下面的关系:

将(4) 式及(6) 式代入方程(3),则得到关于 F(ξ),E(ξ),G(ξ),H(ξ) 的多项式方程。令Fi(ξ)Ej(ξ)Gk(ξ)Hs(ξ)(i=0,1,2,…)(j=0,1)(k=0,1)(s=0,1) 的系数为零,就得到了关于a0,ai,bi,ci,di(i=1,2,…,n)的非线性代数方程组(NAEs)。利用Mathematica软件及吴消元法求解该非线性代数方程组,并将所得的解代入(4)式,即可得到方程(1)的解。
2 Zakharov方程组的精确解
考虑如下形式的Zakharov方程组:

方程组(7)是描写等离子体的高频运动或非线性光波的模型,其中u是离子密度偏差,v是电场强度的慢变振幅,cs是电子-离子热运动速度,α≠0,β≠0,δ≠0,cs为常数。

对(9)式的第一式直接积分并取积分常数为零,则得

在(9)式的第二式中取c=2αq,并把(10)式代入(9)式整理后得

平衡方程(11)式中的最高阶导数项和非线性项,得到n=1。因此,方程(11)的解具有如下形式:
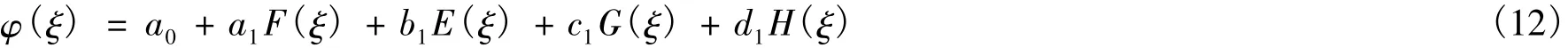
将(6)、(12) 代入(11) 收集Fi(ξ)Ei(ξ)Gk(ξ)Hs(ξ)(i=0,1,2,…)(j=0,1)(s=0,1) 的系数,令它们为零,就得到了关于 k,ω,a0,a1,b1,c1,d1的非线性代数方程组 NEAs,借助计算机代数系统求得如下几组解。
根据的扩展 Jacobi椭圆函数展开法,选取 F(ξ)=g,E(ξ)=e,G(ξ)=f,H(ξ)=h。

情况1:当s=0时,得到方程组(7)的解如下:
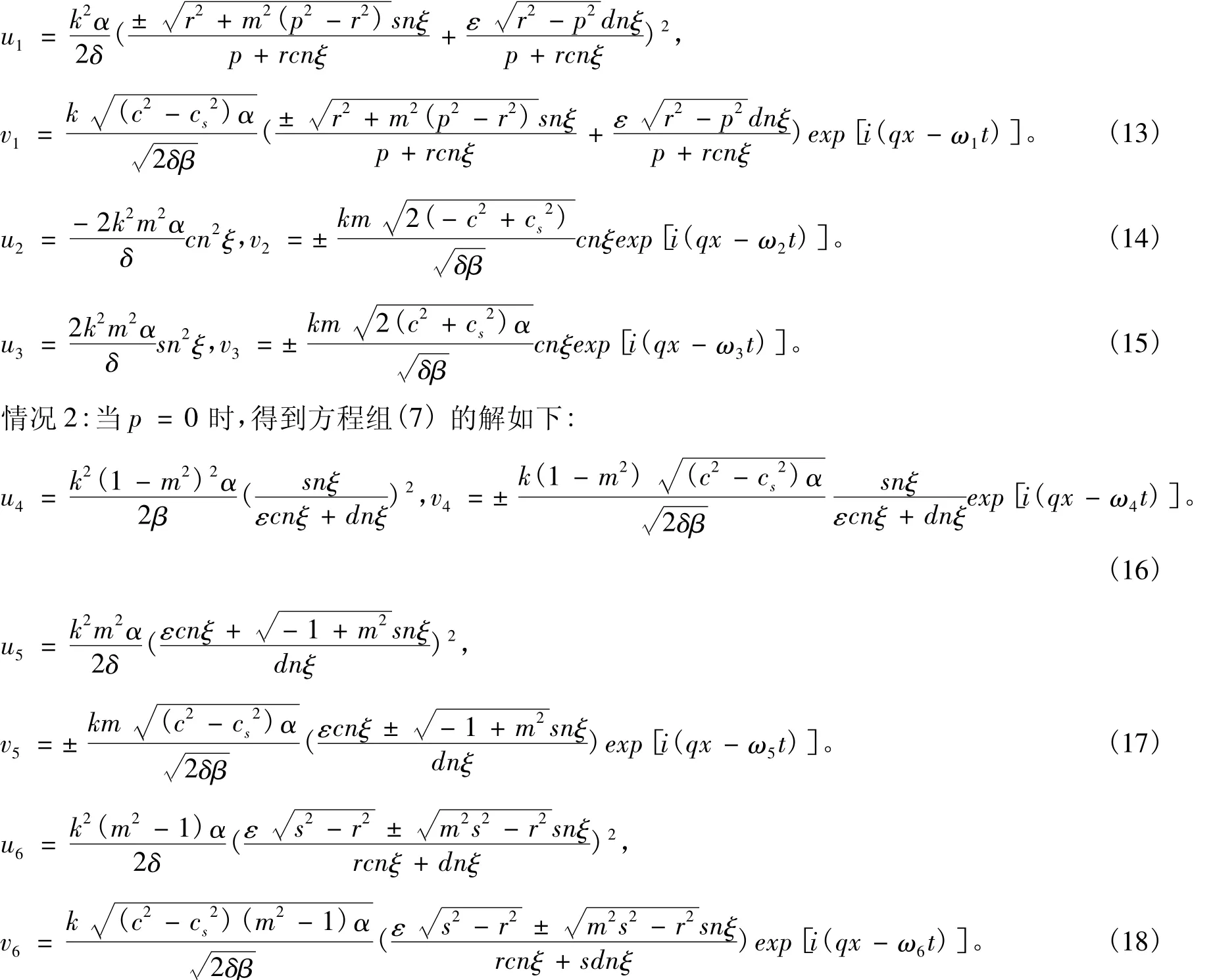
在上式中当r2=s2时,上式中的解变为u4与v4一样的解。
情况3:当r=0时,得到方程组(7)的解如下:24
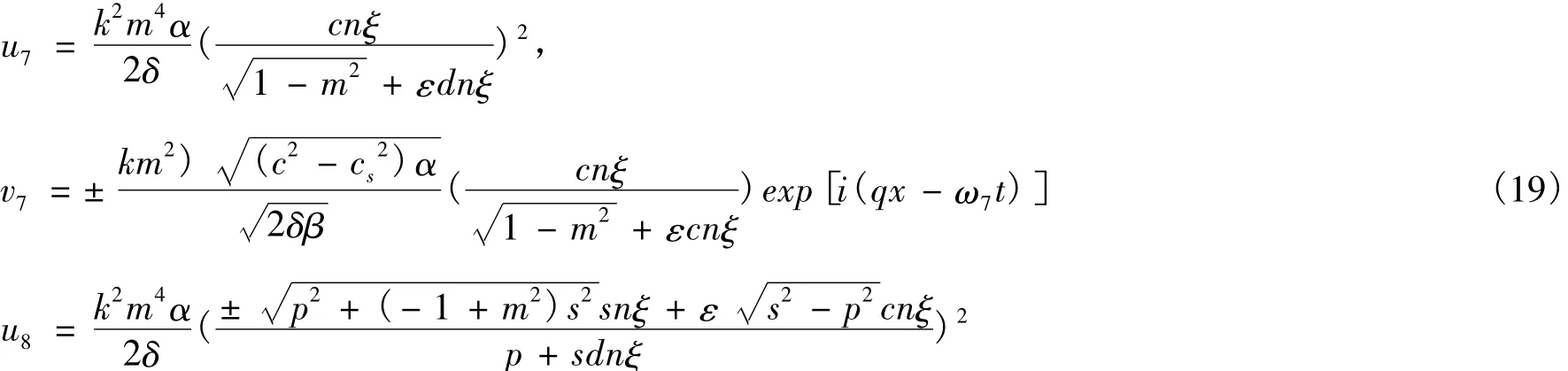

3 结果与讨论
当m→1时,各解分别退化为如下解:

当孤波的运动速度大于离子声速,即c>cs(超声速)时,有β>0,δ>0,此时离子数密度扰动u取正值,当β<0,δ>0时,离子数密度扰动u取负值。当孤波的运动速度小于离子声速,即c<cs(亚声速)时,有β>0,δ>0,此时离子数密度扰动u取负值,当β<0,δ<0,时,离子数密度扰动u取正值。
图 1、图 2 和图 3 分别给出了解 u2,v2和 u'2,v'2、解 u3,v3和 u'3,v'3、解 u4,v4和 u'4,v'4的对照图,图中参数为 α =1,R=0.1,q=4,Cs=1,t=0(其中取 β =1,图中各解中均取“+”),图1 中 β =- 1,在图2和图3中β=1。

图1(a) m=0.8解u2(周期解)
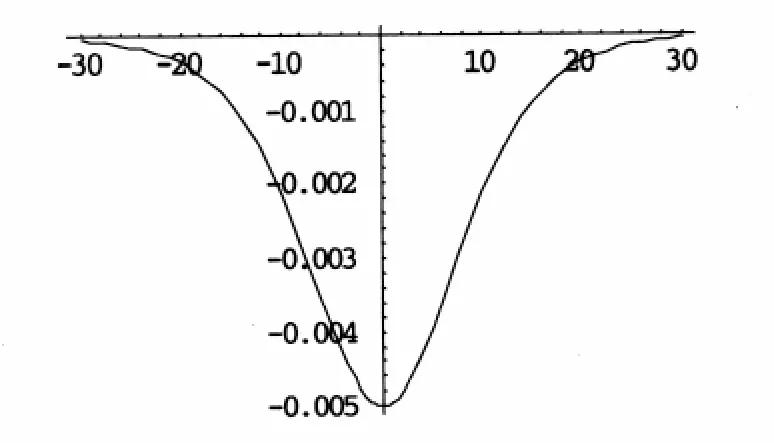
图1(b) m=1解 u2'(孤波解)
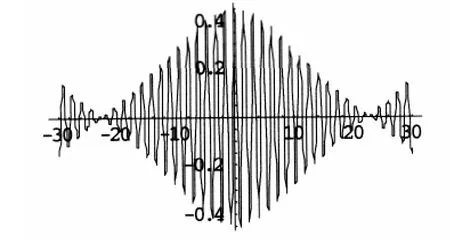
图1(c) m=0.8解v2的实部(包络周期解)
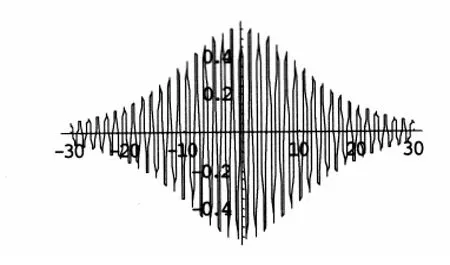
图1(d) m=1 v2'的实部(包络孤波解)
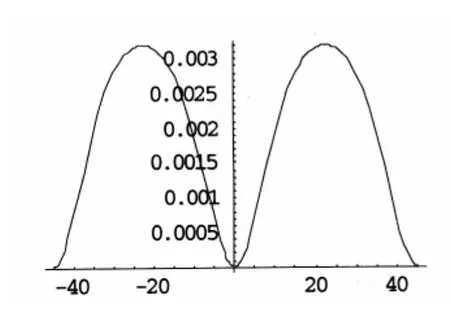
图2(a) m=0.8解u3(周期解)
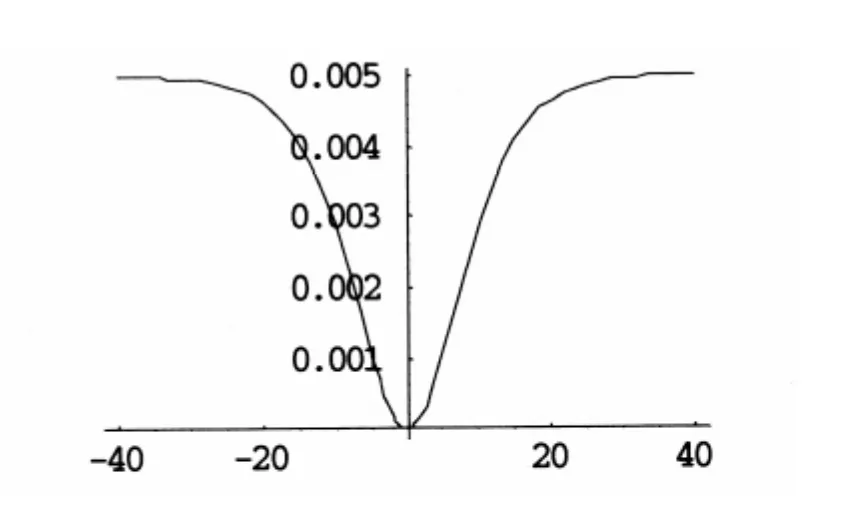
图2(b) m=1解u3'(孤波解)
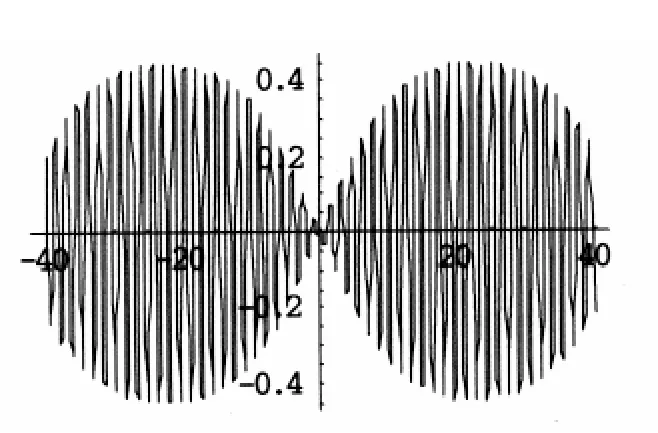
图2(c) m=0.8解v3的实部(包络周期解)
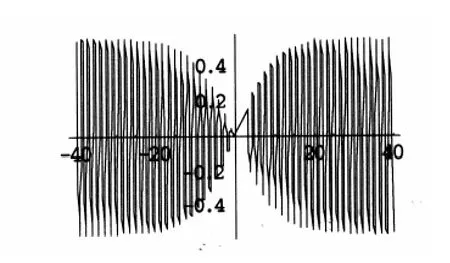
图2(d) m=1解 v3'的实部(包络孤波解)

图3(a) m=0.1 解 u4(周期解)

图3(b) m=0 解 u4'(周期解)
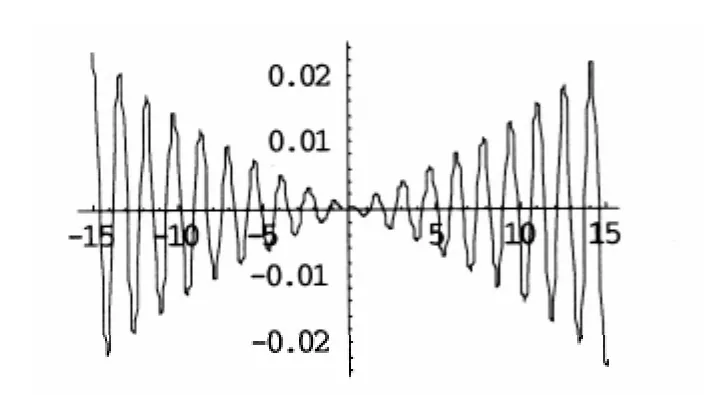
图3(c) m=0.1解v4的实部(包络周期解)
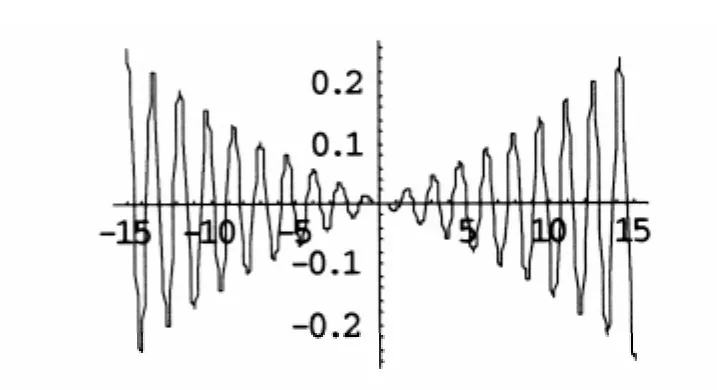
图3(d) m=0解v4'的实部(包络周期解)
4 结论
本文运用扩展的Jacobi椭圆函数展开法,得到了Zakhaorv方程组的若干新精确解,包括周期解、孤波解。从以上求解中可以看出,在Zakharov方程组描述的系统中,离子数密度扰动u和电场强度的慢变振幅v存在各种形式的周期波和包络周期波,这些周期波可退化为孤波。以上求解方法简单有效,有一定的普遍性,可以应用于一大类非线性方程的求解。
[1]Wang M L.Solitary wave solution for varian boussinesq equations[J].Phys.Lett.A,1995(199):169-172.
[2]张桂戌,李志斌,段一士.非线性波方程的精确孤立波解[J].中国科学 A,2000,30(12):1103-1108.
[3]郭冠平,张解放.关于双曲函数方法求孤波解的注记[J].物理学报,2002,51(6):1159-1162.
[4]Zhou Y B,Wang M L,Wang Y M.The periodic wave solution and solitary wave solutions for a class of nonlinear partial differential equations[J].Phys.Lett.A,2004(323):77-88.
[5]刘式适,傅遵涛.一类非线性方程的新精确解[J].物理学报,2002,51(1):10-14.
[6]刘式适,傅遵涛,刘式达,等.Jacobi椭圆函数展开法及其在求解非线性波动方程中的应用[J].物理学报,2001,50(11):2068-2037.
[7]黄定江,张鸿庆.扩展的双曲函数法和Zakharov方程组的新精确孤立波解[J].物理学报,2004,53(8):2434-2438.
[8]吴国将,张苗,史良马,等.扩展的Jacobi椭圆函数展开发和Zakharov方程组的新的精确周期解[J].物理学报,2007,56(9):5054-5059.
[9]豆福全,孙建安,段文山,等.Zakharov方程的多级包络解[J].西北师范大学学报,2006,42(4):38-43.

