地铁车辆限界与设备限界间安全裕量的可靠性再分析——地铁列车与屏蔽门间隙测试

王永坤 程祖国 孙德明 杨凤春杨永立

(1.同济大学铁道与城市轨道交通研究院,201804,上海;2.中国铁道科学院,100844,北京;3.上海鹤之韵轨道交通科技开发有限公司,200333,上海∥第一作者,硕士研究生)

地铁列车与站台屏蔽门间动态间隙安全裕量的设置十分重要,过大过小都将对地铁的安全运营产生严重影响。由文献[1]知,车辆限界与设备限界间留有100 mm的安全裕量是非常安全的。实际上,车辆限界计算时根据影响因素的概率性质考虑了各种可能因素的最不利组合,从计算车辆到车辆最大动态包络线,车辆限界的安全裕量足够大。另一方面,国内多座城市的地铁车站曾发生过乘客滞留在列车和站台屏蔽门间的事件,乘客上下车安全受到严重威胁。这说明列车与站台屏蔽门间存在容纳乘客侵入的空间。那么,列车通过车站时究竟占用多大的空间带?不同可靠度下列车与站台屏蔽门间的剩余间隙为多少?地铁线路上实际运营的车辆与站台屏蔽门间的动态间隙值是多少?可靠度又如何?由这一系列问题,提出了站台区域实际车辆与设备间的间隙测试试验。本文介绍相关试验并基于试验结果做深入分析。

1 站台区域实际车辆与设备间的间隙测试设计

1.1 测试方法与设备

参照限界验证测试方法测试列车与屏蔽门的间隙。测试设备为非接触式激光距离传感器。

测试结果与测点位置(纵向位置、垂向高度)有关。不同测试高度测得的列车与站台屏蔽门间的间隙不同。根据中国人体工程统计资料,普通成年人胸腹部高度约1 300 mm,需要购票的儿童的胸腹部高度约800 mm。因此,测点高度定于站台面以上1 300 mm、800 mm处(限于篇幅本文仅介绍1 300 mm高度的测试结果)。激光距离传感器固定在保证其中心线距站台面高1 300 mm的支架上。测点纵向位置选在各屏蔽门左侧门柱处。

1.2 测试对象选择

屏蔽门选择:随机选择某车站一侧的屏蔽门,1～6号屏蔽门位于直线段,7～28号屏蔽门位于曲线段。试验前屏蔽门未作特别维护。

列车选择:当日在该线路上运行的全部列车。这些列车没有为了间隙测试作特别维护。

1.3 测试内容

测试1 300 mm高度处车体表面与屏蔽门门柱间的横向间距,即列车与屏蔽门的动态间隙(见图1)。

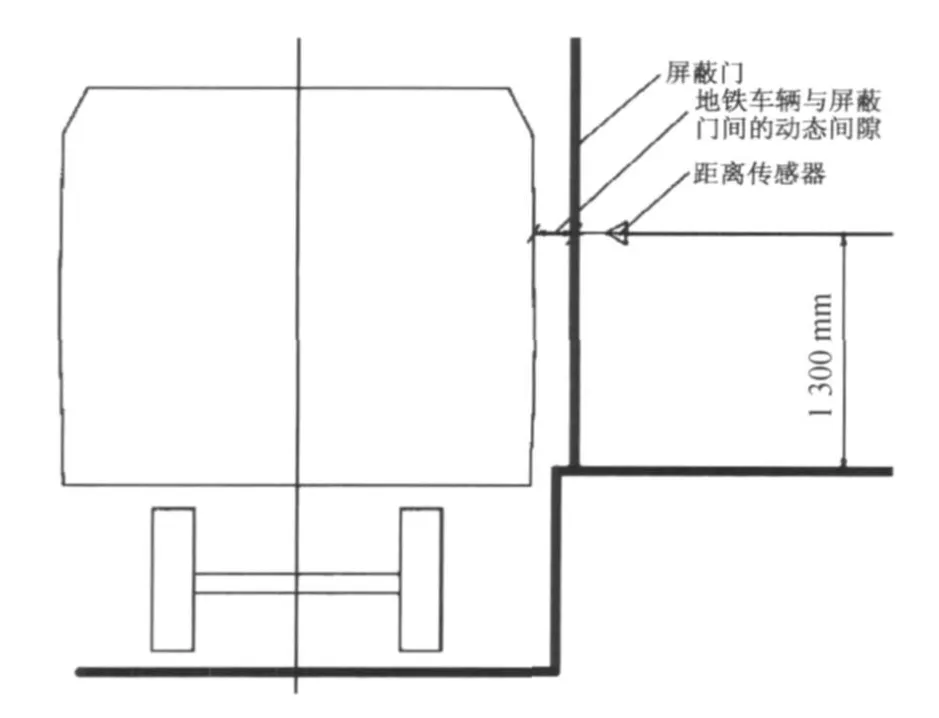
图1 列车与屏蔽门间隙值测试示意图

2 测试结果

2.1 列车与屏蔽门动态间隙测试结果

测试记录了列车进入、停站、离开车站的全过程列车与屏蔽门的动态间隙。测试结果见表1。表1中,间隙测试值为实测的间隙最小值,间隙标准值为CJJ 96《地铁限界标准》在1 300 mm高度处规定的车辆限界与设备限界间的间距[2]。

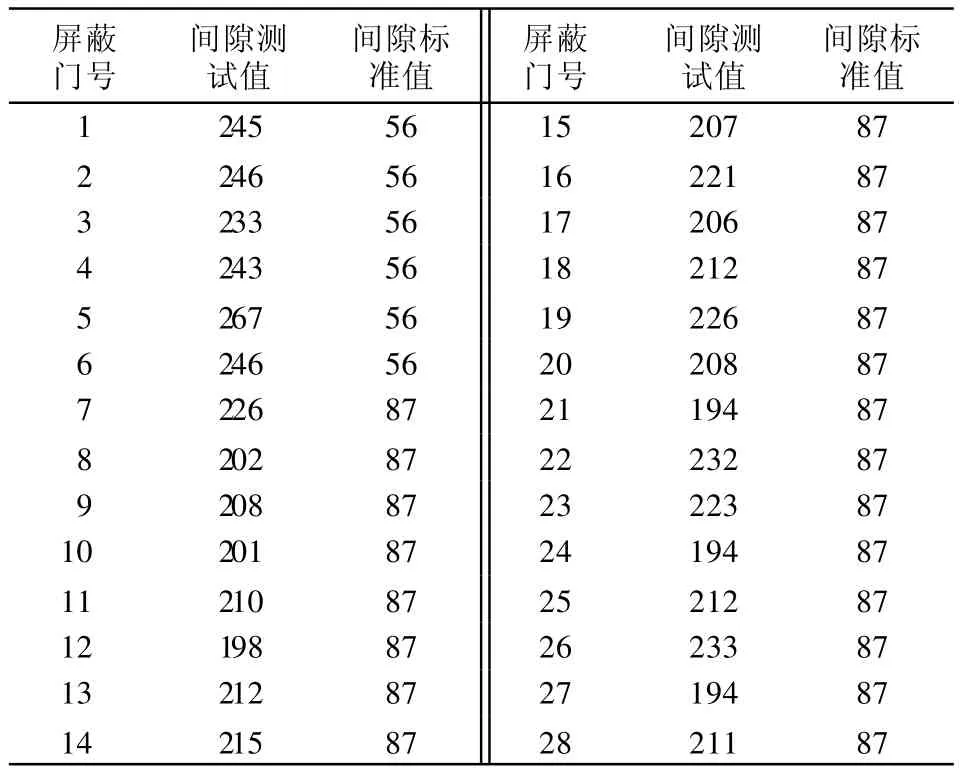
表1 列车与各屏蔽门间隙 mm

2.2 直线站台列车进站时横向晃动量测试结果

在2、3、4、5号屏蔽门处累积测试了11列车进出、通过车站时列车的横向晃动量(见表2)。由表2得,晃动量最小值ΔX min为39 mm,晃动量最大值 ΔX max为70 mm,晃动量均值 μ为49.8 mm,方差σ为9.8 mm。

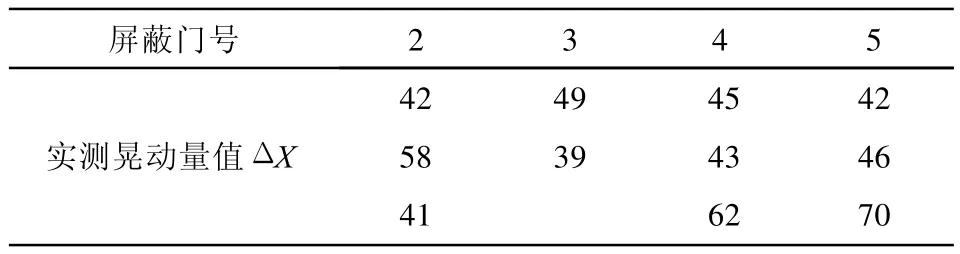
表2 列车横向晃动量 mm

3 车辆限界与设备限界间安全裕量的可靠性分析

分析车辆限界与设备限界间安全裕量的可靠性,其目的在于预计进站列车侵犯屏蔽门的概率。

延用文献[1]的假设,列车晃动量呈正态分布,则

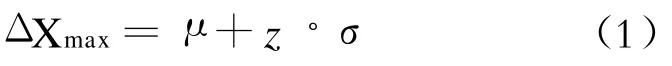
z值在统计学上用来表示标准偏差值,用以描述总体中的个体离均值的偏离程度。本文中z值表征列车侵犯屏蔽门的概率性,z值越大,列车侵犯屏蔽门的概率就越小。通过测试可求出z值;再规定z值,然后求相应的列车晃动量。

在直线站台1 300 mm高度处,实际测得列车的横向晃动量最大值=70 mm,车辆晃动量均值 μ=49.8 mm,方差 σ=9.8 mm 。由式(1)得 z值为2.06。在标准正态分布表中查出实测间隙最大值对应的计算概率为0.980 30;当取z=6时,预计=108.6 mm。

1 300 mm高度处屏蔽门与计算列车车体侧墙表面间隙实测为290 mm。根据上述计算方法,可得到不同z值时预计的列车横向晃动量最大值,从而得出列车侵犯屏蔽门的可能性预计(见表3)。

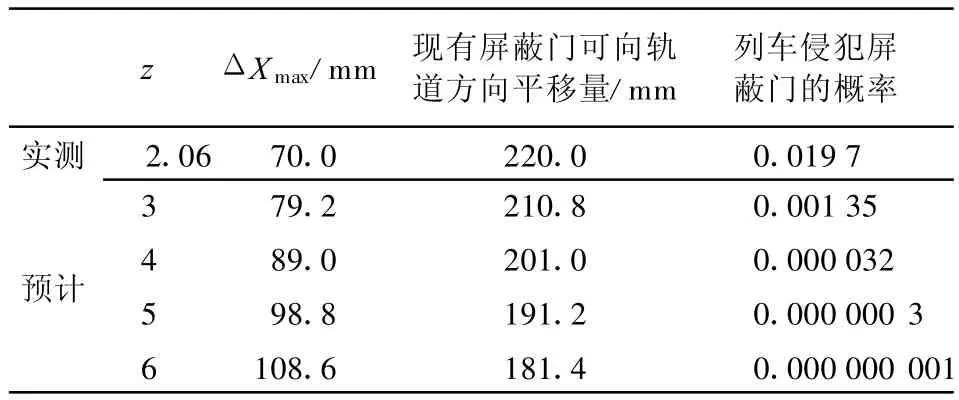
表3 列车侵犯屏蔽门的可能性预计

由表 3可见,假设屏蔽门向轨道方向平移181.4 mm(这时列车的横向晃动量仍保留108.6 mm余量),列车侵犯屏蔽门的可能性也只有0.000 000 001,即列车运行10亿次时,仅有一次横向晃动量最大值会超出108.6 mm。假设3 min通过1列车,每年按365天计算共有131 400次列车经过一扇屏蔽门,则要761年列车才有一次侵犯屏蔽门的可能。由此可见,原屏蔽门处设置的间隙太安全了,可适当缩小。

[1]程祖国,陈薇萍,朱剑月.地铁车辆限界与设备限界间安全裕量的可靠性分析[J].城市轨道交通研究,2004,6(1):26.

[2]CJJ 96—2003 地铁限界标准[S].

[3]杨静敏.德国Bostrab标准中关于城市轨道限界的暂行规范[M].上海:同济大学出版社,1996.