基于Kalman滤波融合算法的某坝基水平位移综合信息提取

郭张军，徐建光，刘佳佳

（1.陕西电力科学研究院，陕西西安710054；2.河南省周口水文与水资源勘测局，河南周口466000）

0 引 言

在大坝自动化监测系统中，坝基水平位移量是反映大坝基础安全性态的重要指标之一，由这些位移资料可建立相关数学分析模型，进而对模型进行物理解释，以分析坝基的工作性态[1]。由于较大的库水压力长期存在，常常根据需要在敏感坝段（如工程地质条件较差）坝基部位布置较多水平位移监测点，以全面了解该坝段各部位的变化情况。即需要多个传感器从不同方位测量同一指标参数，这样就得到多组描述坝基水平位移的时间序列监测资料。传统的方法仅依据某一个监测点的监测数据（即一维时间序列）进行分析，需要人为地从多个监测点中筛选某一个能代表坝基状态的关键监测点的数据进行解析。一方面，对监测点的选择和确定需要开展大量的现场研究；同时，所选的关键监测点能否真正具有代表性还有待讨论，因此，取点往往大多凭经验而定，存在人为性和不确定性。为了避免以点代面，以偏概全，有必要将得到的多个监测点的信息融合成综合信息，然后直接用这个综合信息进行物理解释，无疑将大大提高数据的精度和准确度。已有研究表明[2-5]，Kalman滤波算法能够有效融合观测数据，本文采用基于Kalman滤波的多传感器融合算法实现某坝段坝基多点综合水平位移的信息提取。

Kalman滤波算法是一种多传感器数据融合的核心技术，其通过带有量测噪声的被量测动态系统的状态方程及量测方程，根据量测值提取目标的综合信息，按照其结构可分为集中式、分布式和混合式[6]，考虑到数据量较少，仅采用前两种融合算法。将Kalman滤波理论应用于坝基水平位移监测的数据处理，其实质是建立多个固定的状态方程和量测方程来描述坝基水平位移，并对各监测点采集到的水平位移数据进行跟踪滤波去噪，以获得对被测对象的一致性描述和解释[7]。

1 坝基位移动态监测模型

1.1 位移模型的建立

为便于数学描述，将每一个传感器监测点视为一个运动目标，这样，监测过程可视为对每一个传感器运动轨迹的监测，可用牛顿运动第二定律描述其位移过程：

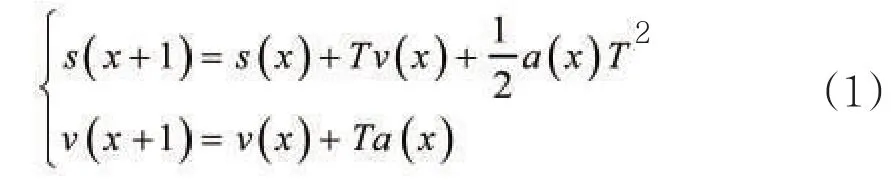
其中，s（x）和v（x）分别表示坝基在x时刻的位置和速度；a（x）表示监测点在x时刻到x+1时刻由于库水位等外界因素变化引起的加速度，它考虑了坝基位移本身和外界环境扰动所造成的不可预测行为。a（x）是服从零均值、方差为Q的正态分布的过程噪声序列，且a（x）和a（y）（x≠y）互不相关，即E{a（x）}=0，E{a（x）a（y）}=Qδ（x-y）。其中δ是克罗内克函数，其特性为k=0时，δ（k）=1；k=1时，δ（k）=0。

1.2 动态监测模型的建立

若将坝基的水平位移和速度视为坝基的状态变量，则由以上分析可建立坝基在变形阶段的状态方程(相当于理论计算模型)和实际量测方程，即动态监测模型

2 集中式多传感器数据融合

在集中式多传感器数据融合系统中，首先按对目标量测的时间先后对测量点迹进行时间融合，然后对各个传感器在同一时刻的目标量测进行空间融合，它包括了多传感器综合跟踪和状态估计的全过程。集中式多传感器数据融合方法是在基础数据层上的融合，信息量损失较小[8]。

假定多传感器信息融合系统中有N个传感器对同一目标进行量测，则全局量测方程为：

集中式多传感器融合系统中所有的传感器数据都直接传送到融合中心来形成统一的系统航迹，将Kalman滤波算法应用于模型，可得全局最优估计，误差协方差为P，具体算法为：

3 分布式多传感器数据融合

分布式多传感器数据融合是对各传感器单独产生的数据进行合成，它的基础是数据相关。分布式多传感器融合系统，即任何一个传感器都是作为整个融合系统的一个模块。一个传感器不受其它单一传感器的限制，形成一个十分松散的结构，一个传感器“插进”系统，或从系统中“拔除”，不至于影响整个系统的正常工作。即使某一传感器“病了”，也不会将“病”传染给其它传感器乃至整个系统[9]。在坝基水平位移监测系统中，由于各个传感器（监测点）在单位采样时间内取值（水平位移监测值）都是唯一的且反映了坝基的位移，因此各传感器产生的位移是相关的。根据有无反馈信息结构，分别进行融合。

3.1 无反馈信息的分布式融合

无反馈的分布式结构，它的每个传感器都要在融合前进行滤波，这种滤波通常称为局部滤波。送给融合中心的数据是当前的状态估计，融合中心利用各个传感器所提供的局部估计进行融合，最后给出融合结果。分布式融合系统所要求的通信开销小，融合中心计算机所需的存储容量小，且其融合速度快，融合方法如下：

3.2 有反馈信息的分布式融合

有反馈的分布式结构，不仅每个传感器在融合前要进行滤波，而且由融合中心到每个传感器有一个反馈通道，需再进行二次滤波，然后进行融合。显然，这有助于提高各个传感器的状态估计和预测精度。当然与无反馈分布式结构相比，它增加了通信量，在考虑其算法时，要注意参与计算的量之间的相关性，融合方法如下：

4 工程实例

4.1 工程概况

陕西境内某拦河坝为混凝土重力坝，2003年投入运行后，总的工况良好,但也出现了值得关注的问题。大坝修建时，对位于河流中央的8坝段的顺河断层F4和F7进行了工程处理，因此该部位工程地质条件较差，为方便日后的监测，在该“敏感”的坝段布置了4个水平位移变形监测仪。近年来，该坝段个别传感器测量的坝基水平位移有增幅较大趋势，且各个传感器采集的数据具有矛盾性等值得关注的问题。

4.2 融合结果及分析

根据近年来8坝段各监测点的坝基水平位移动态实测数据，以2003年监测数据为初始点，历年水平总位移较初始点位移为研究对象，建立坝基水平位移的时间序列，以判断该坝段坝基水平位移变化总趋势。

表1为2003～2008年间8坝段各监测点采集的水平位移监测值（S8-i，i=1，2，3，4）、集中式多传感器融合值（R1）、无反馈信息分布式多传感器融合值（R2）和有反馈信息分布式多传感器融合值（R3）。

表1 2003～2008间8坝段坝基水平位移监测值与融合值(单位：mm)Table 1 :Monitoring values and fusion values of the foundation horizontal displacement of the block 8 during 2003～2008(unit:mm)

由表1可知，近年来除个别监测点外，该坝段坝基大部分监测点的水平总位移具有随时间的推移而增大的趋势，且每年水平位移量呈递减趋势。其中，6年来最大位移量为78.8 mm，发生在S8-2；最小位移量为S8-4的61.9 mm。但S8-3在2003～2007年间，其位移总量随时间增大，但2007～2008年间，却随着时间而减小；同样S8-4在2003～2006年间，其位移总量随时间增大，2006～2007年间，却随着时间而减小，而后的2007～2008年间，却又呈增大趋势，出现反复无规律的变化趋势，即出现了同一时期、同一位置，各个指标对坝基水平位移的评价出现不一致的现象，如图1所示。

分析图1所示的现象，认为与传感器分布位置及其敏感性有关，即可能是由传感器采集数据的冗余性引起的，冗余性容易导致数据的矛盾性。为了消除这种矛盾性，利用Kalman滤波融合方法，分别采用集中式多传感器数据融合方法、无反馈信息分布式多传感器数据融合方法和有反馈信息分布式多传感器数据融合方法进行融合，融合结果见图2。

图1 2003～2008年间8坝段各监测点水平位移变化图Fig.1 Horizontal displacement of the monitoring points on the dam block 8 during 2003～2008

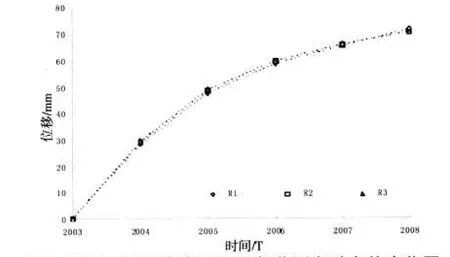
图2 2003～2008年间8坝段各监测点融合值变化图Fig.2 Fusion horizontal displacement of the monitoring points on the dam block 8 during 2003～2008

为了对比分析三种融合方法的精确性，将集中式融合方法与无反馈信息分布式多传感器数据融合方法和有反馈信息分布式多传感器数据融合方法的误差绝对值分别记为ε1和ε2；将无反馈信息分布式多传感器数据融合方法和有反馈信息分布式多传感器数据融合方法的误差绝对值记为ε3，三种方法融合结果的误差绝对值曲线如图3所示。

由图3可知，集中式融合算法与有反馈信息分布式融合算法的最大误差绝对值为2005年的1.4 mm；与无反馈信息分布式融合算法的最大误差绝对值为2005年的1.3 mm，按照每月一次的监测数据采集密度，平均每月数据误差小于0.12 mm，其误差均在允许范围之内，而两种分布式融合算法的误差更是相差甚小。由此可见，三种融合算法具有很高的计算精度，即计算结果均可认为是等价和最优的。

图3 集中式、有反馈信息分布式与无反馈信息分布式融合值间的误差绝对值变化图Fig.3 Absolute error of centralized and distributed method with and without feedback after fusion during 2003～2008

对比图1和图2可知，融合后的数据消除了传感器采集数据的冗余性，消除了融合前数据的矛盾性和不准确性，获得了被测对象的一致性描述和解释。采用Kalman融合方法适当融合后，去除了某些传感器数据的反复无规律现象，在总体上降低数据的矛盾性，这是因为每个传感器的误差是不相关的，融合处理后可抑制误差。

由表1和图2可知，融合后的数据处于各传感器采集数据之间，这是由于不同传感器采集的数据存在互补性。互补性是指经过适当融合后的数据，可以补偿单一传感器的不准确性和测量范围的局限性，这样也就纠正了2007～2008年间监测点S8-3和2006～2008年间监测点S8-4对坝基水平位移的异常反映。由此可见，融合后的数据比其它各组成部分的子集具有更优越的性能，即融合后的效果更加理想。

最后，就实际情况而言，在大坝初期投入运行，且在未经过任何坝基工程补强或自然灾害的情况下，坝基水平位移变化的特点是蓄水初期变化急剧，而后随时间推移渐趋减小，直至稳定[10]。显然，融合后的数据更加符合这一规律。

5 结 语

（1）为了充分利用“敏感”坝段坝基各个监测点的监测信息，提高监测数据的精度，将坝基水平位移监测视为动态监测模型，利用多传感器融合技术来处理坝基水平位移监测信息，对比讨论了基于Kalman滤波的集中式和有无反馈的分布式结构的融合算法。从实例融合结果图2和图3中可以看出，融合后的位移曲线反映了坝基水平位移的整体趋势，反映了将基于Kalman滤波融合算法应用于坝基水平位移监测数据综合信息的提取从理论上是可行的。

（2）经基于Kalman滤波算法的多传感器数据融合方法融合后的数据较为理想，充分利用了各个监测点采集的数据，不仅消除了融合前数据的矛盾性和不准确性，获得了被测对象的一致性描述和解释，而且符合在未经任何坝基工程补强或自然灾害情况下的规律，即坝基水平位移变化的特点是蓄水初期变化急剧，而后随时间推移渐趋减小，直至稳定。

（3）工程实例中，无论集中式多传感器融合算法还是分布式多传感器融合算法，融合结果相差不大，可见三种融合算法的结果均可认为是等价和最优的。2003～2008年，8坝段坝基的整体位移呈递增趋势，但每年平均位移量呈递减趋势，可见坝基与环境的关系正处于逐渐稳定阶段，但由于该部位工程地质条件相对较差，建议以后加强该“敏感”部位的监测，以保障大坝的安全运行。

[1]苏怀智,顾冲时,吴中如.大坝工作性态的模糊可拓评估模型及应用[J].岩土力学,2006,27(12)：2115～2121.

[2]赵红亮,冯夏庭,张东晓，等.岩土力学参数空间变异性的集合卡尔曼滤波估值[J].岩土力学,2007,28(10)：2219～2221.

[3]Willner D,Chang C B，Dunn K P.Kalman Filter Algorithms for a Multi-sensor System[A].Proc.IEEE Conf.Decision and Control[C].[s.l.]:[s.n.],1976.

[4]Lucy Y,Trailovic,Lidija.The optimal order of processing sensor information in sequential multi-sensor fusion algorithms[A].IEEET ransactions on Automatic Control[C].[s.l.]:[s.n.],2000.

[5]苏怀智,吴中如,戴会超.初探大坝安全智能融合监控体系 [J].水力发电学报,2005,24(1)：122～126.

[6]Lawrence A.Klein.Sensor and data fusion concepts and applications[M].Beijing:Beijing institute of technology press,2004.

[7]涂国平,邓群钊.多传感器数据的统计融合方法[J].传感器技术,2007,20(3)：28～32.

[8]郭科,彭继兵,许强，等.滑坡多点数据融合中的多传感器目标跟踪技术应用[J].岩土力学,2006,27(3)：479～481.

[9]王威,周红军,王润生.多传感器数据融合的一种方法[J].传感器技术，2008，22(9)：39～41.

[10]顾冲时,吴中如.大坝与坝基安全监控理论和方法及其应用[M].南京：河海大学出版社，2006.