确实存在正的永续增长率吗?——关于财务/金融理论的基础性思考
张志强,赵全海
(1.中国人民大学 商学院,北京 100096;2.石家庄经济学院 职业技术学院,河北 石家庄 050021)
一、引言
财务/金融理论的基本公理是期望收益和风险决定价值,正如价值评估的折现现金流量(DCF)方法所展示的一样。在DCF方法中,现金流量代表了收益,贴现率则体现了对风险的考虑。为简单起见,学术和实际研究以及价值评估经常将预期风险具体化为经过风险调整的贴现率,而通过初始收益和正的永续增长率相结合来反映未来的期望收益。
Gordon模型(1962)就是一个例子。[1]自20世纪60年代问世以来,Gordon模型一直是应用最为广泛的股票价值评估模型,其形式如下:

其中:D0是上年度的每股红利,D1=D0(1+g)是估计的第一年每股红利,k是市场(投资者)对该股票要求的收益率(代表资本的机会成本),而g是估计的红利永续增长率。
在数学上,Gordon模型要求k>g。在现实应用中,一般情况下或对目前健康的公司而言,g基本都被“理所当然”地估计为一个正的百分数。按照普遍接受的说法,g应该接近于整体经济的长期增长率。然而,这里有一个被长期忽略而又非常重要的问题:确实存在正的永续增长率吗?
也许出乎多数人意料,但稍作分析就不难得出:该问题的答案是否定的。也就是说,确实没有正的永续增长率!如果g代表在未来无限长时间中保持不变的公司股票红利的增长率,那么,它只能是明确的负增长率。为什么?因为经历无限长时间之后,公司必将破产或倒闭。①因此,对于任何一家公司而言,无论它目前看起来多么“健康”,在经历“无限长”时间之后,各种形式的收益(会计收益、营业现金流量、股票红利等等)都将归零。从目前的正价值“平滑”到零,增长率不可能是正的,甚至零增长率也是不可能的。
虽然在折现现金流量计算中,非常遥远的未来现金流量或价值不重要,可以忽略不计,但“近似计算”很难解释增长率由“负”变“正”的合理性。同样,虽然永续增长假设可以简化模型,例如Gordon模型,“模型简化”也很难解释增长率由“负”变“正”的合理性。无论如何,从目前的正值到零,增长率不可能是正的。
另一方面,虽然经济发展会有繁荣和衰退交替,股市也有牛市和熊市交替,但没有人怀疑过长期或永续增长率应该是正的,无论就整体经济或市场而言还是就单个公司或其股票而言。而且,如果每家公司的收入、利润以及股票价值最终都将化为乌有,整体经济的长久或永续正增长又从何而来?
在长久或永久意义上,“正增长率”和“负增长率”似乎都有各自的理由,但它们之间显然存在不可调和的逻辑矛盾。这个由“意外的负增长率”引起的矛盾对传统金融理论和智慧形成挑战。理清这其中的逻辑关系并不容易,本文姑且称之为“ZZ悖论”。
永续增长率或长久增长率的正负问题看似简单,但它是涉及未来现金流量和价值折现的根本问题,而折现计算是财务和金融理论大厦的基石。因此,“ZZ悖论”提出了振动财务和金融理论大厦根基的重大问题。对这个“悖论”的思考和讨论不可回避。本文将基于Moody的各信用等级公司违约数据探讨与ZZ悖论有关的问题。
值得注意的是,虽然在本文中负增长率一再得到证实并应用于相关的分析,这并不意味着我们同意用负增长率替代目前常规分析中的正增长率,也不意味着我们同意按照负增长率进行分析和评估,比如第五部分中很低的价值评估结果。这些分析只是演示“如果”最终金融理论难以推翻“负增长率”,结果会是怎样。我们所以称之为“悖论”而不是结论,就是希望它不会对既有的金融理论造成大的冲击;或者,在对其能够透彻解释之前,可以找到适当的办法避免由此造成的逻辑麻烦。[2-3]无论如何,ZZ悖论隐含着丰富的金融理论和实践意义,例如关于破产、增长率、贴现率、股票定价等方面。
二、不变的增长率是几何平均增长率
容易理解,现实中很难有经济变量会有“不变”的增长率。所谓“不变”的增长率实际是对复杂现实的简化,或者说是一定时期中的“平均”增长率。从数学上讲,有两种常用的方法可以计算平均增长率。一种是算术平均方法,另一种是几何平均方法。
用Vt表示第t期变量的值,则该变量的算术平均增长率(AAG)和几何平均增长率(GAG)可以分别通过式 (2)和式 (3)计算。

用g表示n期中不变的增长率,则V1=V0(1+g),V2=V1(1+g),……,Vn=Vn-1(1+g)。所以,V1/V0=V2/V1=……=Vn/Vn-1= (1+g)。进而, (V1/V0+V2/V1+V3/V2+…+Vn/Vn-1)=n (1+g); (V1/V0×V2/V1×…×Vn/Vn-1)=(1+g)n。
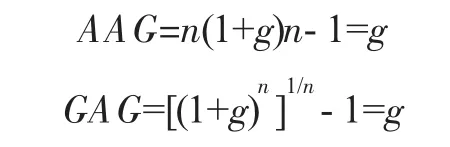
以上的计算显示出算术平均和几何平均计算的一致性。但实际上,除了每年增长率都相同的情况,AAG和GAG的计算结果都是不同的。如果已知各年增长率的标准差为SD,AAG和GAG有如下数量关系:

公式(3)显示出几何平均增长率只与变量的初始值和最终值有关,而与该变量的变动过程无关,如此看来几何平均似乎不很可靠,但实际上它比算术平均更为可靠。例如,某变量从最初的100增加到200,最后又下降到100,根据算术平均,平均增长率是25%。因为最终价值等于初始价值,增长率应该明显是0%,即符合根据几何平均得到的结果。因此,在金融和经济平均增长率的计算中,几何平均处于主导地位。同时,几何平均增长率也符合经济和金融理论中复利增长的假设。
类似地,所谓永续增长率即是在无限长时期中的几何平均增长率。实际上,即使公司可以永远存在下去,人类的智力也无法预测未来无限长时期的增长率。根据前面的分析,在到达无限远之前,目前存在的某公司必定会破产倒闭,这又使预测有了某种可行性。也就是说,在破产倒闭之后到无限远之间相应的现金流量都是零。从目前的正值到未来的“0”,其“年均几何增长率”不难测算。然而,在数学上,这种情况下的年增长率肯定是-100%。为在测算或演示中避免这个统一的“-100%”,本文假定公司在其最后年份中,股票红利或相应的微观变量是一个接近于零的正数,比如是“10亿分之一元”而不是“0元”。
三、破产概率与公司寿命
在长期中,公司每年平均发生破产的概率一定是正数,虽然它也许非常小,但绝对不可能是0或负数。已知这个(小)正的年破产概率,就容易估计公司的期望寿命。例如,以1%作为年破产概率。根据排队论可知,公司平均可能将在第100年破产(=1/1%),因此,公司的期望寿命是100年,虽然该公司的实际寿命也许会长些或短些。
用b表示年破产概率(常数),则公司期望寿命为1/b;而(1-b)代表年生存的可能性。再用B表示连续n年中的累计破产概率,即n年中发生破产的概率。则n年中不破产(即连续n年存活)的概率为(1-b)n。从而n年中发生破产的概率为:[4]

不妨从现实数据中寻找一些直观感受。如表1所示,Moody公司每年都公布为期一年到十年的公司实际累积违约率。[5]但值得注意的是,根据定义,Moody公司的“违约”与本文的“破产”在概念上有所不同。在本文中,“破产”意味着公司寿命结束和股票价值消失,这也符合破产的理论定义和普遍理解。而Moody公司的“违约”除了包括破产,还包括公司发生财务困境的某些情况。所以,违约的范围大于破产,这意味着实际的累计破产概率比表1中对应的累积违约率百分比要小。

表1 Moody公司的历史平均累积违约率(%)
累计破产概率和期望的公司寿命取决于长期不变的年(平均)破产概率。考虑到破产和违约之间的差异,下面取表1中数值的一半作为累计破产概率。根据表1第6列的五年累计破产概率,②通过反用式(5),可以计算出平均的年破产概率,如表2中第1-3行所示。
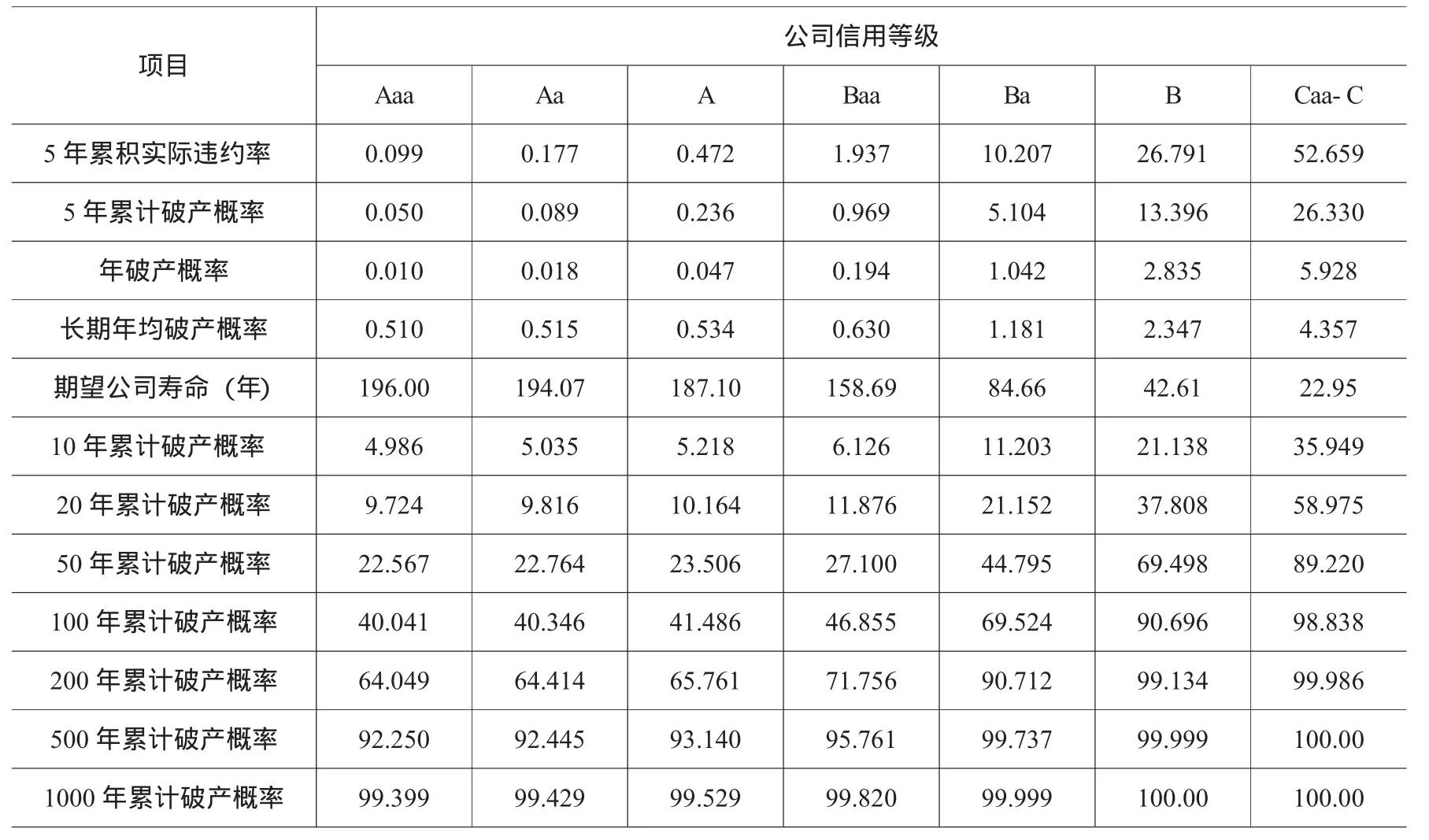
表2 各信用等级公司的期望寿命和累计破产概率*(除公司寿命外,其他单位都为%)
因为所得出的年破产概率将用于计算长期中的累计破产概率,因此,这种年破产概率数据应该考虑长期中的重要因素再加以调整。最相关和最可能的因素应该是公司的信用等级会发生变动,它会直接影响公司将来的年破产概率。因此,上面所得出的表2第3行的年破产概率还要考虑信用等级的可能变化而加以调整。
Norbert Gaillard(2007)根据Moody公司报告的1986年到2006年年末信用等级推算出年信用等级变化率。[7]原始的数据划分为更详细的信用等级,包括Aaa,Aa1,Aa2,Aa3,A1,A2,A3,Baa1,Baa2,Baa3,Ba1,Ba 2,Ba3,B1,B2,B3,Caa1,Caa2,Caa3。根据表1的信用等级合并这些数据,可以得出如表3所示的年信用等级变化率。
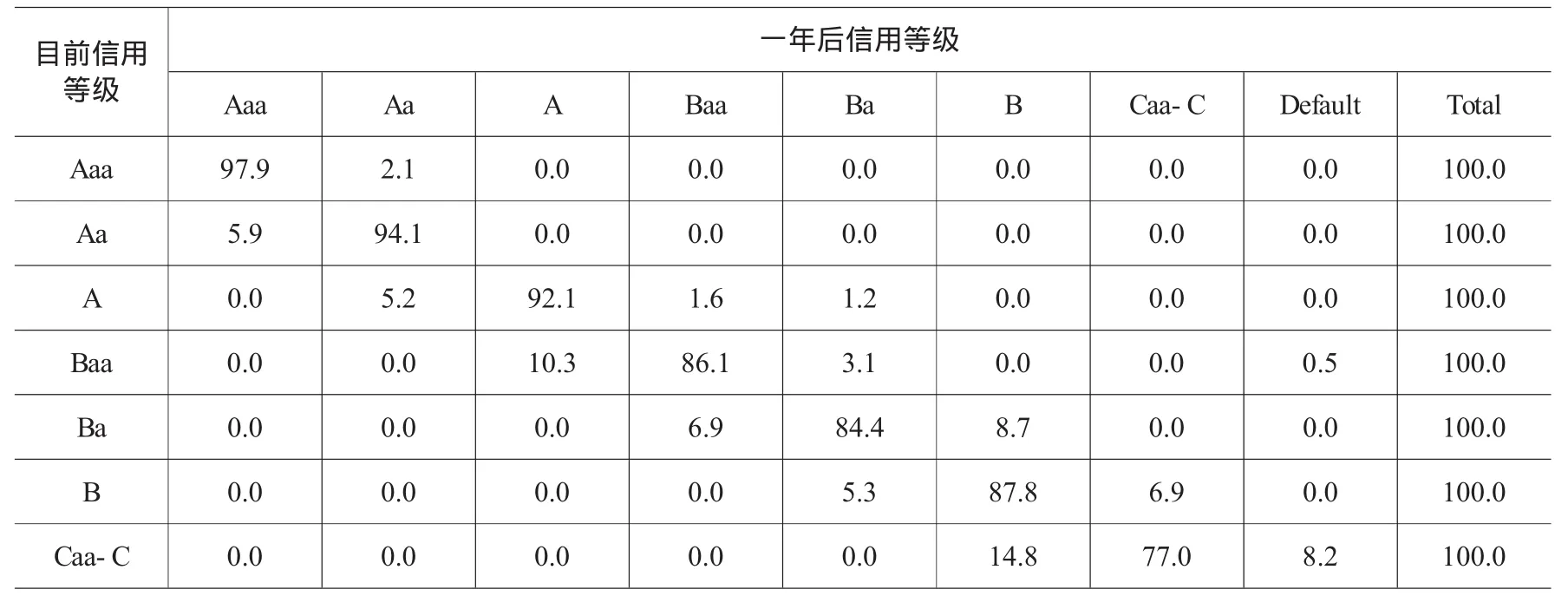
表3 Moody公司年信用等级变化率(%):基于1986-2006年的实际数据计算
根据表3,经过一年,大致有90%的公司会保持其当前的信用等级。假设从长远看公司保持其当前信用等级的概率是70%,或者公司变动信用等级的概率是30%,并进一步假设变动到其他各个信用等级的概率各为5%。③这样,长期平均的(不变的)年破产概率,如表2第4行所示,是行3对应的百分比乘以70%,再加上5%乘以剩余的各个百分比的总和。期望的公司寿命是长期年均破产概率的倒数。各种时期长度中的累计破产概率可以根据式(5)和长期年均破产概率计算得到。
根据表2,A类信用等级(Aaa、Aa、A)公司的期望寿命大约是190年,B类信用等级(Baa、Ba、B)公司的期望寿命是50年~150年,C类信用等级(Caa-C)公司的期望寿命在30年以下。基本上所有的B及其以下等级的公司在100年中破产的概率都接近或超过50%。所有A等级的公司在200年中破产的概率也都超过50%。如果考察期延长到500年,所有等级的公司发生破产的概率都超过90%。如果考察期延长到1000年,所有等级的公司发生破产的概率都超过99%。这可以说基本上反映了现实情况,因为“百年老店”是许多公司可望而不可及的目标,而我们很少能够看到生存超过1000年的公司。[4]曾经威名显赫的Barings银行(1762年到1995年,存在233年)、WorldCom公司(1983年到2003年,存在20年)和雷曼兄弟(1850年到2008年,存在158年)等等,最终都难逃破产宿命。
因此,在应用Gordon模型和其他折现模型时,更为现实的假定是相关的收益或现金流量将持续数十年或数百年;而且在这数十年或数百年中,至少部分时间是负增长,绝对不都是正增长,更不可能永远正增长。
四、公司寿命与增长率
容易证明,在Gordon模型中,增长率g也是每股收益(E)的增长率和股票价值的增长率(即年资本利得)。要计算具体股票的红利“平均”增长率,需要知道当前的红利D0。虽然公司的红利每年波动,有时还可能连续多年为0,但在估计增长率时,通常经过“平滑”得到一个“正常”的D0。不用说,“正常”的D0一定是一个正数。
现在,红利增长率的正负问题已经非常清楚:从当前正的价值到破产时的“0”,无论如何也想象不出一个平均的正增长率。所以,虽然公司发展过程中会有起起伏伏,因为当前值是正的,而最终值是零,不变的增长率在几何平均的概念上只能是负的。基于表2中的期望公司寿命,假定最后的股票红利是“10亿分之一元”而不是“0元”,根据几何平均计算,可以得出各信用等级公司股票的年均增长率,如表4所示。
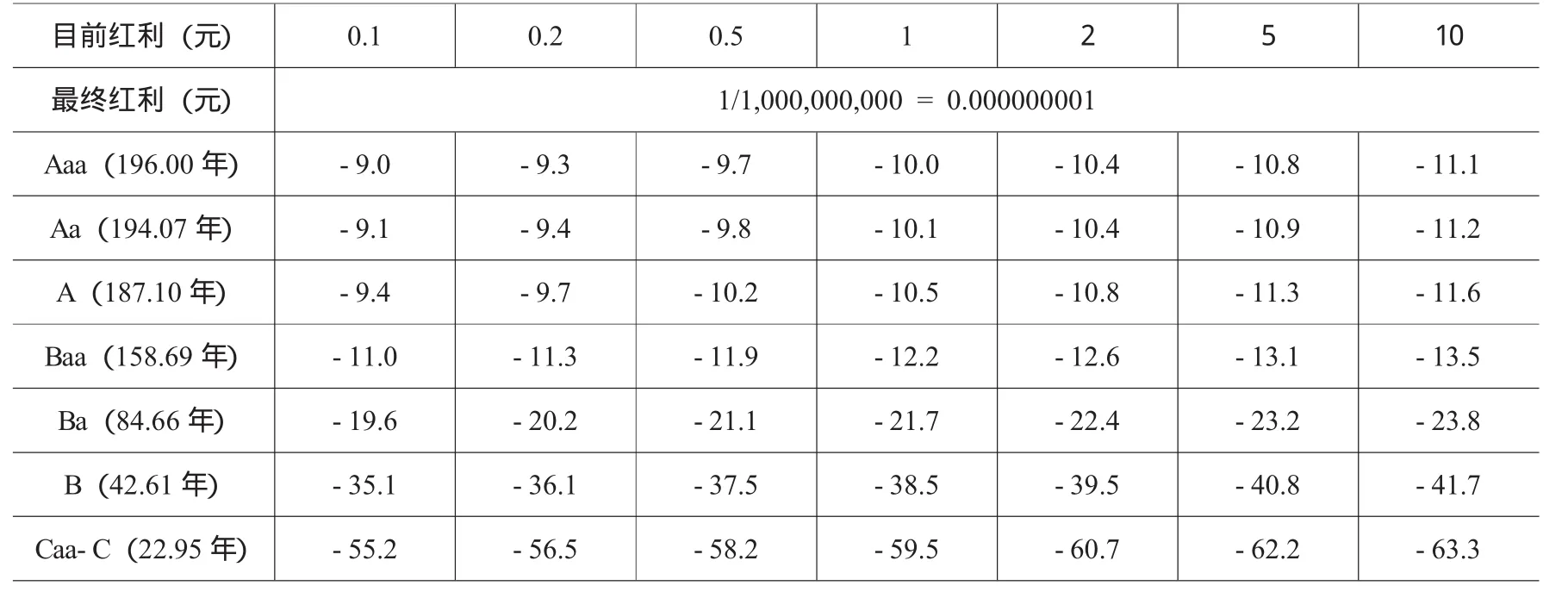
表4 各信用等级公司股票红利的年均增长率(%)
毫不奇怪,表4中没有正增长率。不仅如此,当公司预期寿命较短时,例如Caa-C等级的公司,负增长率的绝对值还会很大。这表明,如果我们想要正确估计红利、现金流量、每股收益以及公司及其股票价值的增长率,必须认真考虑公司寿命的影响;同时,考虑公司寿命的影响,负增长率似乎又是不可避免的。
注意,此处得到的负增长率是在有限时间范围内的平均增长率,与Gordon模型中的永续增长率有所不同。然而,如果考虑时间足够久远,将公司寿命或破产考虑在内,用平均增长率代替永续增长率,不会对价值评估结果产生明显影响。因此,为方便数字演示,下文将在Gordon模型中直接代入这些平均增长率进行计算。
五、负增长率的价值评估意义
幸运的是,当增长率为负时,仍然可以使用折现方法评估股票或资产价值,并且还可以使用Gordon模型。然而,可以想象,如果使用负的而不是正的增长率,评估出来的价值会大大低于原来的结果。本部分中将根据“典型股票”的情况,运用Gordon模型,演示用负增长率代替正增长率对价值评估结果的巨大影响。
根据标准普尔500指数的逐年数据,④从1960年到2007年,S&P 500的复合年增长率(资本收益)是7.12%,年平均红利收益是3.26%,平均年总收益是10.38%。为简化数据,假设典型股票的要求收益率(贴现率)为10%,当前红利(0年)是1元,红利永续增长率为7%。根据Gordon模型,该股票的价值为:
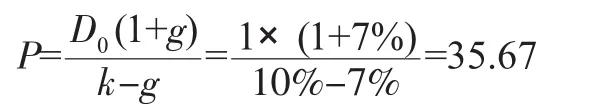
这是根据目前应用Gordon模型的惯例即用“正增长率”进行的价值评估。
现在我们来考虑公司的的期望寿命。根据表2,所有等级公司的简单平均的期望寿命是126.58年,因此我们可以预期典型的公司在第126.58年破产。按照表4的计算,D的增长率(目前D=1)将是-15.1%。将这一增长率代入Gordon模型,股票价值为:
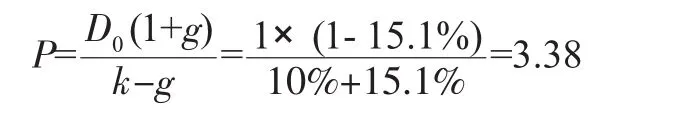
显然,股票价值35.67和3.38之间的差别太大,在目前的金融理论中难以找到恰当的解释。然而,最重要和最迫切的,也许不是如何解释或掩盖这个巨大的差异,而是回答哪个结果是正确的,或者哪个结果更为正确一点。
不幸的是,回答这个问题相当困难。一方面,“3.38元”的价值评估结果为多数人所难以接受,它甚至与投资“常识”不“兼容”。另一方面,7%是S&P500指数整体的增长率,而不是其中典型公司的增长率。由于典型公司的寿命与整体市场的寿命不同,显然说典型公司股票的增长率也是7%就很牵强。在S&P500按照年均7%增长的48年期间,有多少公司破产消失了,又有多少新公司加入进来?因此,以整体市场增长率代表一只典型股票的增长率是不对的。也就是说,很难认为上述35.67的评估结果是正确的。
目前,许多研究都根据市场或经济总体的数据估计单只股票的数据,并应用于相应股票的价值评估。上述评估结果的巨大差异提醒我们,整体市场的数据并不适用于单只股票;进一步,应该重新考虑整体市场研究的局限性和公司研究的重要性。特别是当涉及股票红利、每股收益、现金流量等微观变量的增长率时,整体市场的结论不可以简单地推广到单只股票;由于在足够长的时期中,“整体”与“个体”的增长有“正”与“负”的差异,单只股票的增长率也不能根据整体市场的增长率“调整”出来。
为获得更多的直观感受,依据表4各信用等级公司的增长率,进一步评估相应各公司的股票价值。假定目前每股红利为1元,贴现率为10%,考虑公司寿命的永续增长率是各种具体的负百分比而不是正的7%,这种情况下股票价值的评估结果及其与目前流行价值评估结果(35.67元)的差异如表5所示。

表5 考虑公司寿命的股票价值评估结果
正增长率(g=7%)导致股票价值的明显高估。根据表5,多数公司股票价值被高估90%左右。这意味着考虑公司期望寿命的价值评估与现有价值评估之间有不可调和的差距。以A信用等级的公司为例,如果当前年每股红利为1元(短期内不会有大幅度的变化),在期望寿命是190年的情况下,根据表5的计算,股票价值只有大约4.4元!虽然很难想象有投资者愿意相信或接受这样的价值评估结果。然而,除了与现有价值评估理论和智慧相背,负增长率和更低的价值评估结果在概念和逻辑上似乎是无懈可击的。
六、贴现率是否已经考虑了破产损失?
如前所述,金融理论的核心公理是期望收益和风险决定价值。Gordon模型通过风险调整的贴现率来考虑期望风险,通过初始价值和正的永续增长率来反映期望收益,这完全符合“期望收益和风险决定价值”的原理。那么,是否破产风险已经通过贴现率k得到考虑,从而不再需要根据破产预期调整估计的增长率呢?果真如此,则正的永续增长率就可以得到合理解释了。
遗憾的是,事实并非如此。风险是不确定性,或者在金融和经济意义上,风险是期望收益的不确定性。破产预期实际上有双重作用。一是减少收益,二是增加风险。前者包括由于破产停业引起的预期损失,由本文前面的负增长率来反映。后者是指破产发生的不确定性,由贴现率k的增量来反映。
破产风险是指破产发生的不确定性,这种不确定性当然会增加破产之前相关的收益或现金流量的不确定性。理论上,应该根据这样的不确定性调整要求或期望收益率k。实践中多运用资本资产定价模型(CAPM)或其变型(例如Fama/French的三因素模型[8-9])来估计k。在确定期望收益率或风险补偿率时,CAPM及其变型仅考虑系统风险,如由一个或若干个beta所代表的风险;而假设在合理分散投资的情况下,所有单只股票的非系统风险将互相抵消。然而,关于破产风险是否属于系统风险,理论上还处于争论不休的状态。[10]许多实证研究也表明,破产风险在市场上没有得到应有的高收益补偿。所以,根据CAPM及其变型得出的k充其量考虑了破产风险,但肯定没有考虑期望破产损失。
可以肯定的是,损失或者预期损失不是风险。从价值评估角度看,损失实际上是负的收益。预期损失属于影响期望收益而不是风险的项目。即使贴现率考虑了破产的不确定性或破产风险,最后的期望破产损失还须由增长率来考虑。因此负增长率还是不可避免的。
无论如何,如果保持永续增长率的正号,而通过增加贴现率来考虑所有风险以及期望破产损失,计算一下贴现率将增加到多高的水平将是非常有趣的。下面根据前面的“基准案例”做这样的计算。注意贴现率是10%,当前红利是1元,并有正的永续增长率7%。
首先,假设破产损失通过负增长率得到考虑,并且所有风险,包括破产风险,都考虑到贴现率k中。与前面的分析相同,由于公司的期望寿命是126.58年,评估结果为:
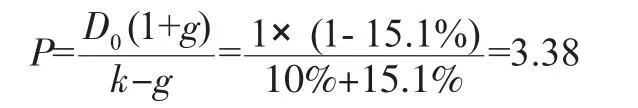
其次,根据Gordon模型,k=[D0(1+g)]/p+g。已知当前红利及其增长率和股票的当前价值,就可以求得隐含的贴现率k。现在,根据股票价值3.38元和“正的永续增长率”(7%)而不是负增长率(-15.1%),可以求出考虑相关的风险也考虑破产损失的隐含贴现率k:
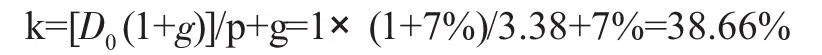
因此,作为一家典型的公司,如果将预期破产损失考虑在内,贴现率k应该接近38.66%。同理,可以得出各信用等级公司的隐含贴现率k,如表6所示。
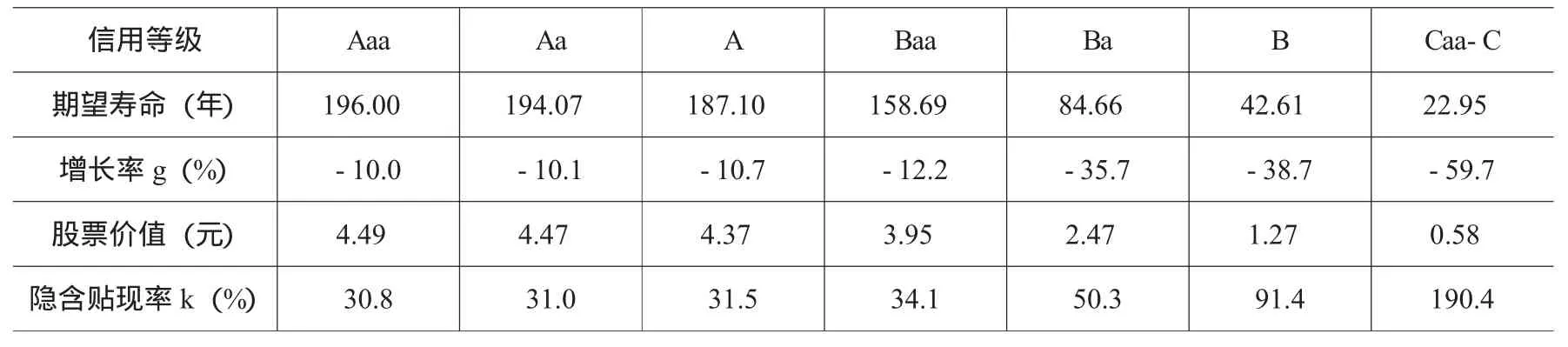
表6 考虑破产损失的增长率g和贴现率k
在表6中,在所有信用等级情况下,隐含的k都远远高于现有常规的10%左右的水平。A信用等级公司隐含的k都超过 30%。B信用等级公司隐含的k为35%~90%;C信用等级公司隐含的k是190%。而所有信用等级公司隐含的k的简单算术平均是65.65%。这些“超常高”的贴现率进一步证实,现实中经常采用的大约10%的贴现率并没有考虑破产损失。既然常规的贴现率并没有考虑破产损失,正的永续增长率就仍然没有得到合理的解释。
从上面的分析可以看出,在价值评估中,破产损失的影响远大于破产风险。如果我们在评估股票价值时忽视了破产损失,那么,在贴现率中破产风险是否得到考虑实际上已经不太重要了。在公司财务领域,破产成本是指由于破产概率或破产风险的增加(而不是破产本身)而减少的公司价值。破产成本的更为狭义的概念是指在破产过程中发生的相关费用,例如律师费、审计费以及与债务重组等操作有关的其他间接费用,如更高的利率、更高的保险费等。显然,就财务健康的公司而言,与期望破产损失相比,期望破产成本要小得多。
张允和和周有光的妹妹是同学,两人由此相识。两家都是望族,但周家此时已经没落,一度连周有光念大学时的学费都交不起,所以张允和常笑称自己是戏曲看多了,有“落难公子后花园”的情结,不仅没有嫌弃周家家道中落,反而认定了周有光是个“落难公子”,想去搭救他一把。
一般而言,公司有两类风险:一是经营风险,表现为公司收益和价值随着公司内外条件的变化而波动;二是破产风险,表现为在债务到期时,如果公司价值低于其债务帐面价值(资不抵债),公司不得不终止经营。如果公司资本结构中没有债务,它就只有经营风险,而没有破产风险和破产成本。所以,破产成本是与举债筹资和破产风险相对应;破产损失是与总风险相对应,包括经营风险和破产风险。可以理解,在评估股票价值时,应该考虑所有风险而不仅是破产风险,即应该考虑破产损失而不仅是相关的破产成本。
与破产成本相比,破产损失不仅价值大,而且也更为明显和简单。然而,奇怪的是,在学术和实际领域,破产成本受到了更多的关注和研究。迄今为止,股票价值评估基本上没有关注破产损失。由此可以怀疑:目前的金融研究中可能有重要的盲点。当然,破产成本在有些题目的研究中更为重要,比如融资中关于资本结构的选择。然而,这很难成为在评估股票价值时可以不考虑破产损失的理由。
股票的价格反映了投资者对股票未来风险和增长前景的判断。由于10%的贴现率和7%的增长率以及以此为基础评估出来的股票价值有实际数据支持,这也许暗示着投资者对破产损失也不关心。不论是什么原因造成了投资者对破产损失采取这种态度,但这种态度决定了他们的行为(买或卖股票),而他们的行为又决定了市场上的股票价格及其变动。在目前实证研究成为金融研究主流的情况下,市场数据作为研究的样本数据,进一步决定了研究结论和学者的观点,而学者的观点又会回到市场,进一步加强投资者无视破产损失的态度。这个无休止的循环也就是投资者的“非理性”与学术领域的“误研究”之间循环强化的过程。这也许可以解释为什么股票市场上如此大量、广泛而持久地存在泡沫。从上述学术与实践之间的循环可以看出,由于强调现象之间的“统计”联系而不是本质关系,实证研究对市场泡沫的形成和持续实际上是起了推波助澜的作用。
七、对正的永续增长率的强行解释
有一种世界观认为,真理往往为少数人所掌握;在多数情况下,社会上多数人的观点是错误的。另一种世界观认为,存在的即是合理的,因而多数人的观点总是正确的。ZZ悖论提出的增长率正负问题也许“过于创新”,暂时只能为少数人所接受;但同时,在“不牵强”的逻辑下,又很难解释“正永续增长率”这个“多数人的观点”。下面尝试以“存在的即是合理的”为世界观,强行解释多数人所习惯的“正永续增长率”。虽然严格讲这不符合科学和学术精神,但期望因此会有新发现。
由于存在的即是合理的,可以认定目前的股票价格是或基本是正确的。比如,前面“典型股票”的价格就应该是35.67元。一个可以强行解释的理由是,这个35.67元的价值即是股票在该公司存续期间所有红利及最终价值的现值总和。Moody公司的现实数据表明,这个“典型公司”的预期寿命为126.58年。所以,35.67元的价值即是该股票在这126.58年间的红利现值。一般而言,由于这是一家目前典型的健康公司,可以预期其股票红利在未来一定时期中会有正增长;但是,在公司破产之前的或长或短的时期中,股票红利会有负增长。为简单起见,假设这家公司预期寿命为126年;前63年股票红利处于“匀速”上升状态,后63年股票红利处于“匀速”下降状态。当然,到第126年,股票价值下降为零,而股票红利下降到接近于零的水平,假设为1/1,000,000,000元。由于当前股票红利为1元。假设“匀速”上升时的年增长率为g1(>0),“匀速”下降时的年增长率为g2(<0)。则公司未来126年中各年的股票红利如表7所示。

表7 典型公司寿命期间各年的股票红利(元)
根据上述条件可得:
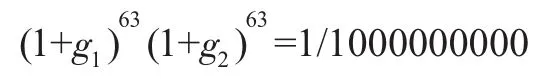
并且:
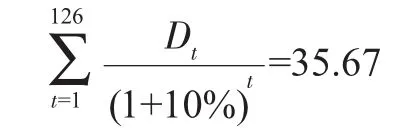
其中,D为第t年的股票红利,如表7所示。注意上述两个方程中只有两个未知数,即g1和g2,解得:g1=7.8%,g2=-35.6%
由于应用Gordon模型或永续增长率时:
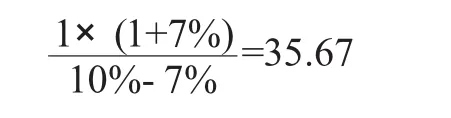
即35.67的价格中隐含的永续增长率为7%。因此,这意味着正的永续增长率7%是根据前63年平均每年增长7.8%和后63年平均每年增长-35.6%“平滑”出来的。如果认为上述关于这家典型公司的未来增长情况假设是合理的,那么,就可以认为7%的正永续增长率也有合理性。这样就强行解释了正的永续增长率。也就是说,正的永续增长率是隐含在公司未来时期上升和下降过程中的永续增长率。
然而,在现实评估和定价操作中,所谓的“正的永续增长率”经常被轻而易举地“预测”出来,没有这么复杂和困难,基本没有考虑公司还有下降以至消失的过程。在上述例子中,如果不考虑股票红利还会下降以至于永久性消失,而简单地将7.8%直接作为永续增长率,则股票价值为:
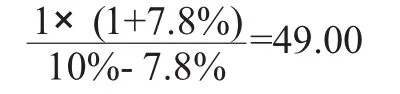
与根据隐含的(也许是正确的)永续增长率7%评估的35.67相比,评估价值增加了13.33元即增加了37.37%。显然,简单地将公司近几年或几十年的增长率看作永续增长率(目前的评估操作)会造成巨大的评估误差。由此可以判断,由于连公司的破产和寿命都没有考虑,目前价值评估中对增长率的“预测”很可能只是装点门面的摆设而已,而相应的价值评估的可信度就可想而知了。这也许就是股票市场时常“莫名其妙”大起大落的原因——因为没有人认真估算当然也没有人知道股票理论上值多少钱!
八、结论
在足够长的时期中,公司难免破产。无论当前价值多高,在公司破产时,红利或股票价值都将接近于零。尽管破产之前的时间长度和波动情况会有差别,但红利从当前的正值变动到接近于零,在几何平均或复合增长逻辑下,年均增长率只可能是负的。依据Moody公司报告的各信用等级公司的实际违约率,经过多方面的讨论,除了在假设目前股票价格正确的前提下强行解释为股票价格的内含增长率,本文最终没有找到正的永续增长率存在的适当理由,虽然这与目前人们的“习惯认识”和“理论假设”相反。不仅如此,最终分析发现,包括Gordon模型在内,通过折现现金流量评估股票价值的实际做法还缺乏可靠性。
在本文的写作过程中,美国的次贷危机演变成为世界性的金融危机,也导致了世界各国股市的大跌。虽然每次股灾或金融危机都有其独特的直接原因,但是,一个更深层的共同原因也许是金融资产和股票价值的高估。一次又一次的危机已经表明,我们的金融理论和实践长期存在根本性的缺陷。这与ZZ悖论所带来的逻辑挑战不谋而合。这种巧合也许是在提醒我们:现在是从根本上反思金融理论和金融研究的时候了。可喜的是,ZZ悖论带给我们的除了挑战还有多方面的启发。由于ZZ悖论是对金融理论和实践的根本性疑问,它所启发出的新发现将源源不断地更正、补充和完善我们现有的金融理论;这些也都将有利于破解现实金融谜题,解决评估、定价和决策难题。
注 释:
①严格讲,破产与倒闭在概念上是有区别的。在本文中,我们强调的是公司最终总会以某种形式(破产或倒闭)消亡,同时其股权价值和现金流量将下降为零。所以,不强调破产与倒闭在概念上的区别,而简单以破产称之。同样,也许公司还会被其他公司收购,但即便如此,也难免最终随收购公司一起消亡。所以,请不要因为现象或过程的多样性而影响了对本文概念的本质理解。
②选择其他列不会造成计算结果的很大变化。注意本文中与负增长率有关的多数观点或结论有充分的逻辑或概念支持,文中的计算主要是演示而不是证明,具体而言是从多角度演示负增长率或ZZ悖论的影响,因而在假定或数据方面的某种程度的不精确不会对结论有大的影响。所以,为方便演示和读者理解,在基本符合实际的情况下,我们将尽量采用简单的假设和计算。
③注意,这里未来信用等级变化到7个信用等级的概率之和为70%×1+5%×6=100%。并且注意,如表3所反映的实际情况,公司更有可能变化到与原来相近而不是更远的信用等级,因此假设变化到每个信用等级的概率相等就相当于夸大了信用等级的变化。另一方面,信用等级在10年(大致代表典型的“长期")中没有变化的概率是90%10=34.87%,这种情况下假设其为70%实际上是缩小了信用等级的变化。这样两个假定的偏差大致可以相互抵消,同时会使得计算更加简单。同样注意,这里将“70%”向下调整,同时将“5%”向上调整将增加A信用等级公司的破产概率,而减少C信用等级公司的破产概率。
④本段中的数据是由作者根据Aswath Damodaran提供的数据计算得出的。原始数据见Aswath Damodaran(2008),yearly data of the S&P 500 from 1960 to 2007,http://pages.stern.nyu.edu/~adamodar/New_Home_Page/datafile/spearn.htm。
[1]Gordon,M.J.The Savings Investment and Valuation of a Corporation[J].The Review of Economics and Statistics,1962,(1):37-51.
[2]张志强.ZZ金融发现[M].北京:对外经济贸易大学出版社,2008.
[3]张志强.理论市盈率与理论市净率[J].中国会计研究与教育,2009,(1).
[4]Jorge A.Chan-Lau.Fundamentals-Based Estimation of Default Probabilities∶A Survey[R].IMF Working Paper,2006,06/149.
[5]David T.Hamilton and Richard Cantor.Measuring Corporate Default Rates[R].Special Comment of Moody,November,2006.
[6]Richard Cantor,David T.Hamilton,Jennifer Tennant.Confidence Intervals for Corporate Default Rates[R].Special Comment of Moody,April,2007.
[7]NorbertGaillard.Moody’ sSovereign Ratings: 1918-1939 and 1986-2006 Compared[R].Chaire Finances Internationales Working Paper,August,2007.
[8]Fama Eugene F.and French Kenneth R.Common risk factors in the returns on stocks and bonds[J].Journal of Financial Economics,1993(33),3-56.
[9]Fama Eugene F.and French Kenneth R.Multifactor explanations of asset pricing anomalies[J].Journal of Finance,1996,51.
[10]Dichev,Ilia D.Is the risk of bankruptcy a systematic risk?[J].Journal of Finance,1998,53.

