基于过程集成的电磁轨道炮脉冲电源多目标优化
范昭楠 于歆杰
(清华大学电机工程与应用电子技术系电力系统国家重点实验室 北京 100084)
1 引言
电磁轨道炮是使用电磁加速技术发射弹丸的一种电能武器。其基本工作原理是在导轨中通入电流,在导轨周围产生磁场,而电枢在安培力的作用下向前加速[1-3]。
本文首先简要介绍电磁轨道炮多级电容储能脉冲电源系统模型和负载模型,然后在系统仿真软件Simplorer V7下搭建脉冲电源系统,用VHDL语言编写负载模型,仿真观察发射过程中系统各部分参量变化。进而基于过程集成的思想,利用多目标优化算法NSGA-II求解系统最佳的参数配合,使得在初始储能一定的条件下,得到最快的发射速度和最高的系统效率,同时满足加速度上限的约束。
2 脉冲电源系统模型
本文中脉冲电源系统采用多级电容储能形式,共由20个脉冲形成单元(Pulse Forming Unit,PFU)组成5级的脉冲电路,每级的PFU数量依次为8、2、3、3、4。本文中仿真将每个PFU模块进行封装,便于参数设置,界面简洁。
图1为PFU的内部结构,由两个储能电容并联后串联触发晶闸管,再与一续流二极管并联,然后连接到脉冲形成电感,通过同轴电缆引出,图中两个电容并联等效为一个电容及等效串联电阻(ESR),脉冲形成电感和同轴电缆模型共同由一电感和电阻串联组成[4-7]。
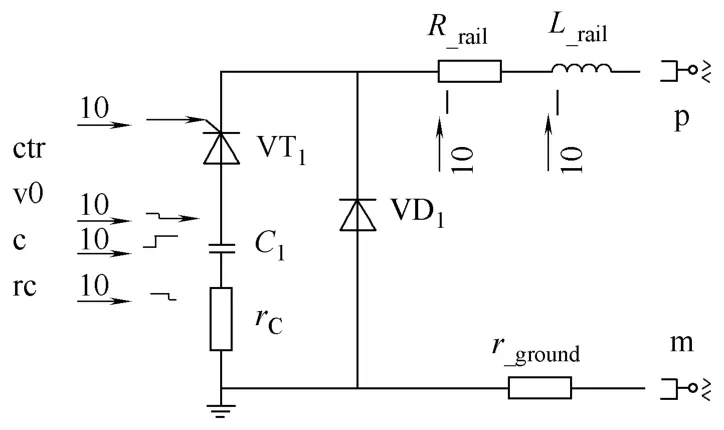
图1 PFU内部结构Fig.1 The inner structure of PFU
每个电容值 2mF,等效串联电阻 1µΩ,晶闸管(图 1中 VT1)导通电压 3.6V,导通电阻 225µΩ,二极管(VD1)导通电压3.6V,导通电阻 480µΩ,等效串联电感(图中 L_rail)值56µH,等效串联电阻值(图中R_rail)29mΩ。接地电阻(图中r_ground)1µΩ。
图2为电磁轨道炮发射装置的等效电路,图中Rg(x)表示导轨电阻,Lg(x)表示导轨电感,Rs表示电枢电阻。
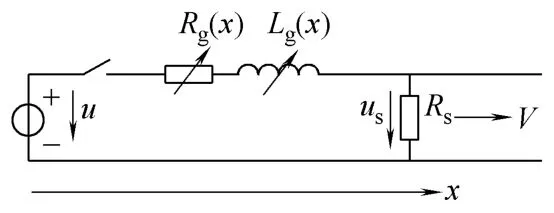
图2 负载等效电路Fig.2 The equivalent circuit of the load
上述各量的计算表达式如下[8]:
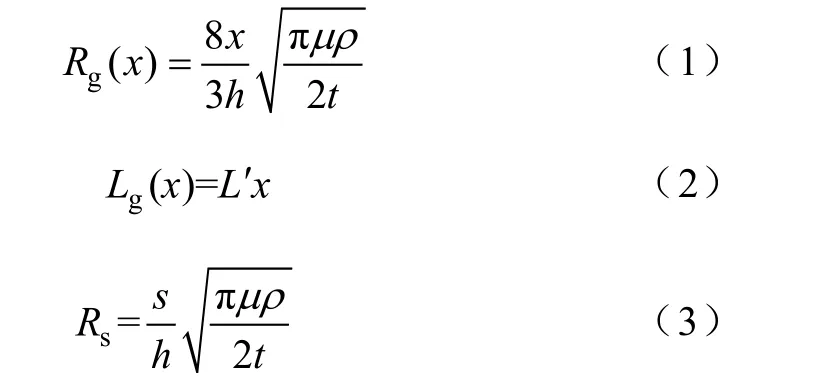
式中 x——电枢移动距离;
t——时间;
h——导轨高度;
µ——材料磁导率;
ρ——等效电阻率。
由于电流扩散效应,此处ρ 是电流的方程[8],其表达式为

电枢及弹丸的加速度与电路的关联方程由能量守恒关系得到,进而积分得到速度与位移方程[9]

有了以上的关于导轨炮的描述以后,就可以利用 VHDL语言建立其模型用于仿真。这里µ取1.26µH/m,h取 0.1m,s取 0.53m,L′取 1.1µH/m,ρ0取 1.7E-8Ω·m,β 取 3.6E-16Ω·m2/A。
3 仿真结果分析
图3为上述的导轨炮模型在 Simplorer 下的仿真电路图,由于对每段电源封装成模块,可以看到尽管有 20个 PFU,但仿真电路仍然简洁明了。每段电源的 PFU内部参数及导轨炮模型参数如前所述,仿真步长取值范围为1~100µs,观察其负载的电流和相关变量的时间函数。
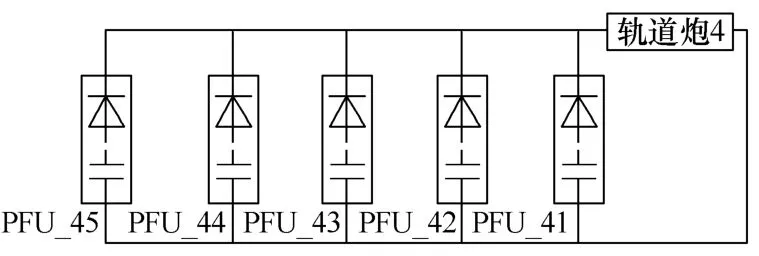
图3 轨道炮仿真模型Fig.3 The simulation model for the railgun
本文分别进行了3kV、6kV、10kV三种充电电压等级的仿真,每两个储能段的触发间隔都取1ms,导轨长度5m,弹丸质量45g。
表1给出了在三种充电电压下的仿真结果。从仿真结果可以粗略看出随着充电电压,也就是初始储能的升高,弹丸发射速度和系统效率都有所上升。

表1 仿真结果Tab.1 Simulation results
下面以 10kV时的仿真结果为例,给出相关波形。图4为发射过程中导轨以及各储能段的电流分布,可以明显看出导轨电流是由5个储能段的电流叠加而成。

图4 电流分布Fig.4 Current distribution
4 系统参数优化
从以上的仿真结果来看,弹丸在出膛时导轨电流仍比较大,也就是说系统剩余能量较多,因此有必要对相关参数进行优化,找出在初始储能一定的情况下最佳的参数配合。
对设计者来说,希望获得尽可能高的发射速度和系统效率,同时也要考虑导轨及电枢材料对加速度(电流)的限制,因此实际上这是一个带约束的多目标优化问题。
通过多次数值计算找出上述问题的最优解是不太现实的。本文提出基于过程集成的思想,使用优化软件iSIGHT,能够应用专门解决多目标优化问题的优秀算法来求得该问题的 Pareto最优解。
在优化算法的选择上,作者选择了NSGA-II—采取精英策略的非支配排序遗传算法,NSGA-II是在 NSGA的基础上改进得到的一种多目标优化算法,其最突出的特点是采用了快速非支配排序和排挤机制[10]。
图5为利用 iSIGHT9对上述问题优化的流程图。利用 VB Script作为中间控制程序,启动数值仿真,输出目标参数;iSIGHT首先读取目标参数,然后启用优化算法,修改运行参数,执行VB Script程序得到下一次仿真结果。
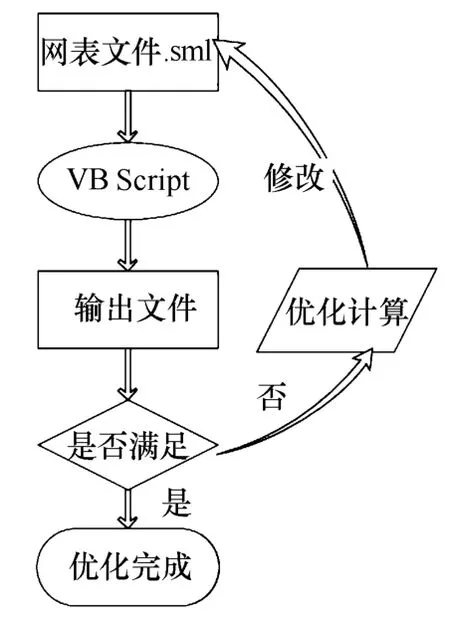
图5 优化流程Fig.5 Optimization flowchart
表2列出了本文中优化模型的相关参数和具体数值,其中触发间隔指的是每两个相邻储能段的触发间隔范围。

表2 优化模型Tab.2 Optimization model
表3为优化算法NSGA-II的参数设置,包括种群规模,进化代数和交叉分布指数。

表3 优化算法参数Tab.3 The parameters of the algorithm
分别对 3kV、26kV、10kV三个充电电压等级的模型进行优化,表4为三种电压下优化目标在优化前后的对比。
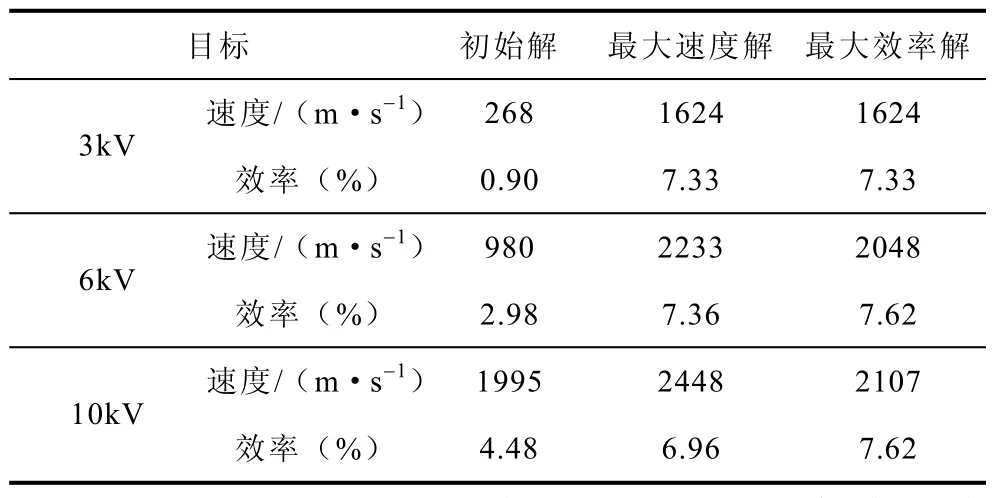
表4 优化结果对比Tab.4 The comparison of the optimization results
表5列出了优化参数初值和Pareto解集中的单个目标最优解对应数值。图6为它们优化后的Pareto解。
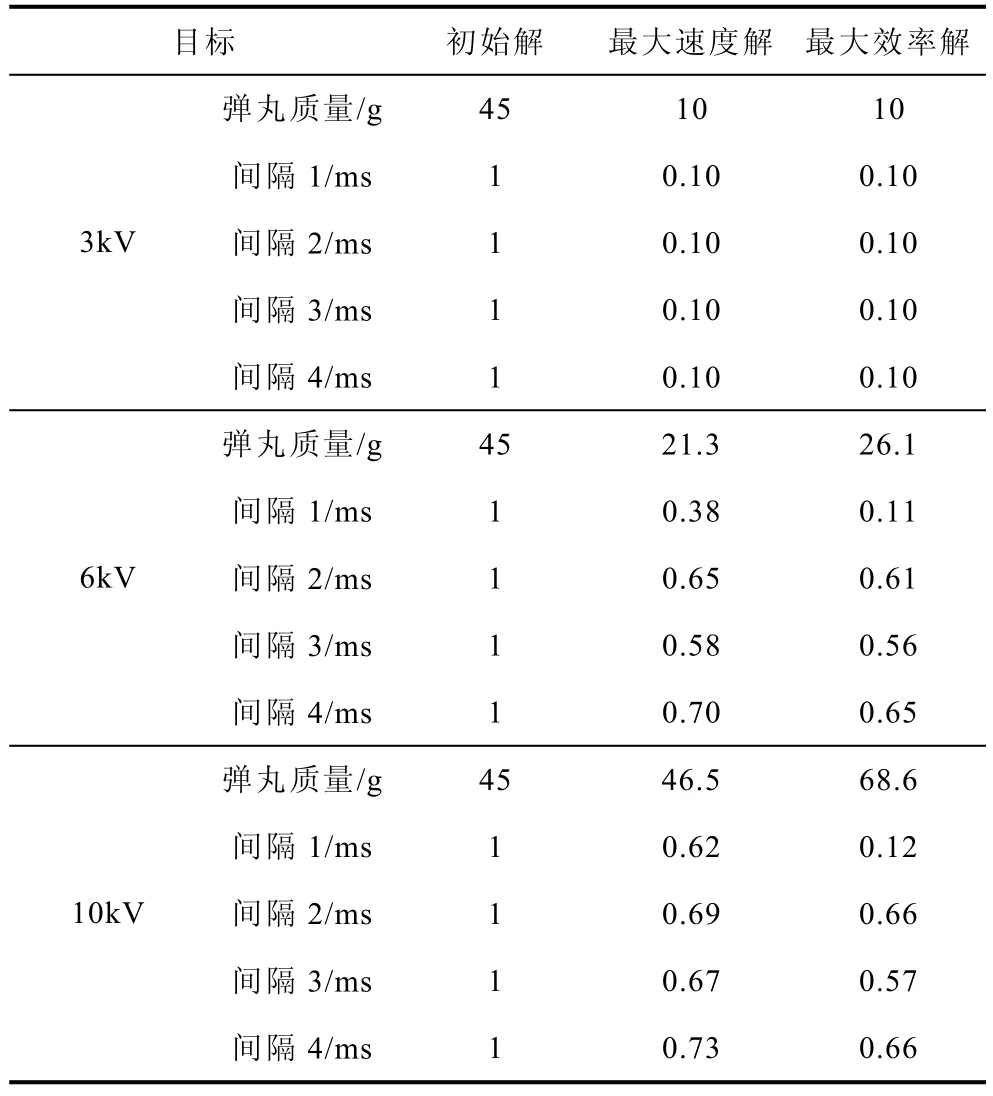
表5 优化参数对比Tab.5 The comparison of the optimization parameters
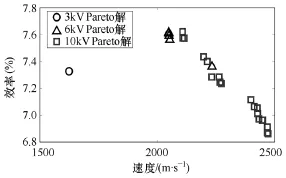
图6 3kV、6kV、10kV Pareto解对比Fig.6 The comparison of the Pareto set for 3kV,6kV,10kV
通过图6可以看出,利用遗传算法NSGA-II优化可以找到在一定条件下的最佳配置方式。并且电压越高,Pareto解越优秀,多样性也较好,意味着设计者权衡发射速度和系统效率时有更多的选择空间。当然也要看到,10kV时的速度和效率已经比6kV没有明显提升,但其发射的弹丸质量更大一些。
优化目标是速度和效率,而电压一定时,效率只取决于弹丸能量:质量和速度。速度又可以看作是加速度曲线的积分面积,所以分别研究 Pareto解和加速度、质量的关系。
首先看加速度曲线。仍以 10kV电压的系统为例,给出三种参数下弹丸在发射过程中的加速度波形,如图7所示。
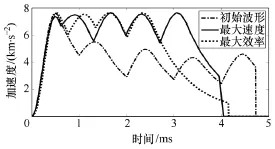
图7 10kV加速度比较图Fig.7 The comparison of the different acceleration curves for 10kV
可以看出最大速度曲线和最高效率曲线都是尽量维持在其上限附近,也就是都要求各储能段的触发尽可能集中。需要指出两条曲线对应的质量是不相同的,最佳效率解对应的质量更大。
对最大速度来说,理想情况是加速度曲线为一个以其上限为高的矩形,而触发间隔最短使得曲线迅速上升并尽可能维持在其上限。对最高效率来说,触发间隔最短就能使得运动早期阻抗较小时电流就上升到上限,阻抗损耗较小,同时出膛时电流已经较小,剩余能量低。所以无论速度还是效率都要求触发间隔在各自质量下尽量短。
然而也要看到,尽管都取的是最短触发间隔,但由于最佳效率解对应的质量比最佳速度解大一些,图 7中最佳速度和最佳效率的加速度曲线有所不同。下面讨论质量对速度和效率的影响。
图8为10kV双目标优化得到的所有Pareto解与电枢质量的关系。可以看出,在Pareto解集范围内质量和两个优化目标呈现出一定的线性关系,和效率正相关,但和速度负相关。
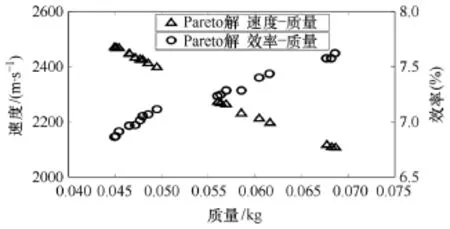
图8 10kV Pareto解质量-速度、效率图Fig.8 The mass-speed, efficiency diagram of the Pareto set for 10kV
当然也要看到质量过小时,触发间隔必然更加疏松,就使得加速度曲线波峰之间的“凹坑”很大,同时导轨长度又有限,甚至可能储能段还没能全部触发弹丸就出膛了,所以就导致速度不高,效率则更低了。这和直观感觉中弹丸质量越小就能发射的越快是不一致的。
加速度约束对系统性能有重要影响,限制了弹丸发射速度和系统效率。在一定范围内,加速度上限越高,Pareto解会越优秀[11]。
5 结论
(1)利用系统仿真软件Simplorer可以方便地建立电磁轨道炮模型,实现发射过程的电路暂态分析。使用优化软件 iSIGHT,嵌入多目标优化算法NAGA-II,实现了对轨道炮带约束的多目标优化问题模型的优化。
(2)对本文的脉冲电源系统,弹丸最大发射速度和系统最高效率的要求体现在触发间隔上是一致的,都是要求各储能段间的触发间隔最短。
(3)一般来说,最大发射速度和系统最高效率对弹丸质量的要求是不一致的,最高效率要求的弹丸质量要大于最大发射速度的质量要求。随着充电电压的降低,二者对应的最佳质量都随之降低,同时趋于一致。
需要指出,通过以上分析,可以发现脉冲电源拓扑结构对系统性能也有重要的影响,如对这 20个PFU的分段数,以及每段的PFU分配,但在本文的方法中无法实现,还需要进一步的探索和发现。
[1]Harry D Fair. Electromagnetic launch science and technology in the united states enters a new era[J].IEEE Transactions on Magnetics, 2005, 41(1): 158-164.
[2]Richard A Marshall, Wang Ying. Railguns: their science and technology[M]. Beijing: China Machine Press, 2003.
[3]Pascale Lehmann. Overview of the electric launch activities at the French-German research institute of saint-louis(isl)[J]. IEEE Transactions on Magnetics,2003, 39(1): 24-38.
[4]McFarland. A long-range naval railgun[J]. IEEE Transactions on Magnetics, 2003, 39(1):289-294.
[5]Ian R McNab, et al. Develop of a naval railgun[J].IEEE Transactions on Magnetics, 2005, 41(1): 206-210.
[6]Satapathy, et al. Design of an 8-MJ integrated launch package[J]. IEEE Transactions on Magnetics, 2005,41(1): 426-431.
[7]Harry D Fair. Electric launch science and technology in the unite states[J]. IEEE Transactions on Magnetics,2003, 39(1): 11-17.
[8]Deadrick F J, et al. Magrac-a railgun simulation program[J]. IEEE Transactions on Magnetics, 1982,18(1): 94-104.
[9]史正军. 高功率脉冲电源的仿真与优化设计[D]. 北京: 清华大学, 2008.
[10]Kalyanmoy Deb, Amrit Pratap, Sameer Agarwal, et al. A fast and elitist multi-objective genetic algorithm:NSGA2[C]. KanGAL Report No. 200001. India,2000.
[11]Shi Zhengjun, Yu Xinjie. Two-objective optimization design for pulsed power supply[J]. IEEE Transactions on Magnetics, 2009, 45(1): 525-530.

