计及寄生参数效应的铁氧体共模扼流圈二端口网络的建立
王世山 谢少军 金 艳
(南京航空航天大学自动化学院 南京 210016)
1 引言
扼流圈是EMI滤波器的主要组成元件,其在电路中的表现形式对滤波器的性能具有重要影响[1]。一般地,干扰信号对滤波器的侵入按差模和共模两类通道来分析。建立扼流圈的共模和差模二端口等效电路能较方便地研究扼流圈及其与滤波器中其他元件的配合问题。
理想的扼流圈对差模信号表现出零阻抗,对共模信号表现出极高的感性阻抗。但实际上,由于材料的非理想性,制造的分散性和线圈绕制的非对称性,不仅理想扼流圈难以达到,而且它在不同的频率表现出不同的阻抗特性,即等效的二端口网络各支路不再是常数电感、电容或电阻,可能是随频率变化的等效参数或者是不同性质参数一定形式的组合。因此,准确建立滤波器的二端口网络对研究滤波器的特性以及改善其性能指标具有重要的意义。
对 EMI滤波器在计及寄生参数条件下的特性展开系统研究也是近 5年才引起研究人员的兴趣[2-5],其中国外以美国Virginia理工学院和州立大学Fred C. Lee教授领导下的研究成果处于世界领先地位[2-3],而国内浙江大学开展了相关的研究,且取得了一定的成果[4-5]。前者的研究主要着重于滤波器互有寄生参数的提取和消除,对扼流圈自有寄生参数仅以差模电路为例展开研究,采用测量阻抗的方式拟合得到以三个参数——电阻、电感和电容组合的扼流圈电路,但尚未以二端口方式表示,且等效的电阻与频率无关。后者的研究采用在不同组合条件下利用测量阻抗的方法,在一定假设条件下得到差、共模等效电路,将研究频率分为不同的段,在每一段内各参数仍为常数。虽然这些研究机构取得一定的成绩,但基本基于实验的手段,无法理论上考虑扼流圈某些材料属性,不利于进一步完善滤波器特性。
已有研究成果虽然未提取扼流圈共模电路的寄生参数,但参考电感器集中参数的研究方法[6-8],则可以建立扼流圈的集中参数模型,也可以将集中参数等效为二端口网络。
如欲对扼流圈等效的二端口测量其阻抗或导纳矩阵,则需要对源端或负载端实现“短路”或“断路”。由于频率较高时源端或负载端不能实现严格的“断路”或“短路”,所以不能对二端口的阻抗或导纳矩阵进行准确测量,而通过测量二端口在阻抗匹配条件下的散射参数可以确定其等效阻抗[9]。文献[10-11]虽然也采用测量散射参数的方法测量滤波器各参数,但是测量的均是滤波器差模电路各元件间的互有寄生参数,尚未发现有采用测量散射参数来确定扼流圈二端口网络参数的文献。
综上所述,建立计及寄生参数效应的扼流圈二端口模型对改善滤波器性能以及更好的优化系统性能具有重要意义。已有研究文献均是基于实验测试,提取差模电路等效参数,无法考虑材料特性对滤波器性能的影响,不利于指导滤波器的设计。
鉴于如上原因,本文将以“谐振频率法+有限元法”建立扼流圈差、共模二端口模型,即建立扼流圈静电场模型,采用有限元数值计算扼流圈二端口模型中的电容参数,通过测试谐振频率得到差模电感。建立扼流圈时谐磁场模型,计算得到磁心等效电阻和电感,在测试谐波频率的基础上,得到共模电路的杂散电容。最后,对所建立的模型与采用散射参数间接测试的阻抗进行比较。
2 “谐振频率+有限元法”建立扼流圈二端口网络原理
2.1 差模干扰信号二端口等效
扼流圈差模干扰信号电路是指扼流圈每个端口的电流大小相等、方向相反(见图1)。考虑到扼流圈两部分线圈结构尽可能相同,仅绕制时方向相反,所以理想情况下磁心内部的磁场几乎互相抵消,表现为磁心的等效电阻和电感为零。但由于磁心磁导率为“有限值”,所以线圈有少部分磁力线泄漏于外空气以及导线本身具有的电感,形成差模电感Ldm,该电感基本为一个常数。
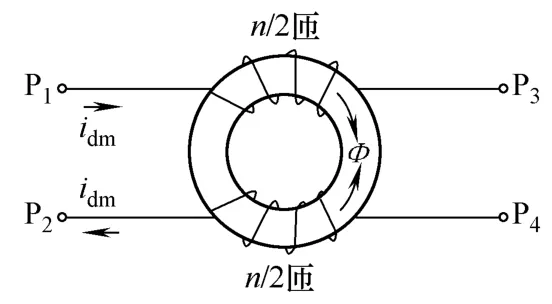
图1 扼流圈差模干扰信号Fig.1 DM noise signals of choke
虽然磁心等效电阻几乎为零,但由于导体的集肤效应,导线交流电阻随频率的增大而增大[12-13],表现为差模电路中等效电阻Rdm。
考虑到扼流圈线匝绕制较紧密,且在差模干扰信号通道时各线匝电位不相等,所以线匝之间的部分电容最终表现为杂散的寄生电容,对滤波器的性能有一定的影响。这些寄生电容在二端口模型中等效为输入输出之间的电容和两部分线圈之间的电容,分别以Cdm,p和Cdm,c表示。
因此,考虑线圈漏磁场时等效的差模电感Ldm、导线交流电阻Rdm、线匝杂散电容Cdm,p和Cdm,c的二端口等效电路如图2所示。

图2 扼流圈差模二端口等效电路Fig.2 2-port equivalent circuit of DM for choke
2.1.1 导线交流电阻Rdm
图2中导线交流电阻仅与导线所处的形状和磁场强度有关,与磁心内是否具有强的磁场无关,所以可以参考单个电感器交流电阻的方法计算该值[6-8,14]。对单层导线组成的扼流圈
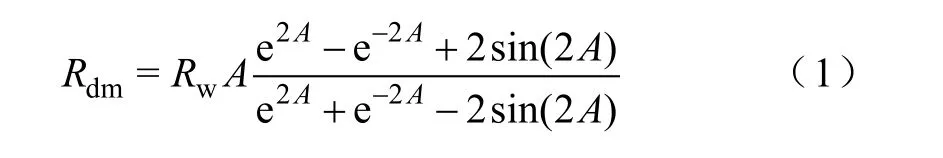
式中,Rw为导线直流电阻;A为系数,对圆导线

式中,d为导线直径;p为相邻导线间的距离;δm为导线在频率为f时的透入深度

式中,ρw为导线的电阻率。
另外,导线等效电感
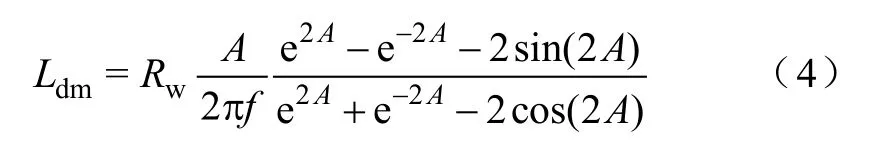
2.1.2 杂散电容Cdm,p和Cdm,c
杂散电容对差模电路高频特性的准确性有重要影响,文献[4]通过阻抗测量的方法提取了这两个杂散电容,其方法为:将P3、P4开路,测量低频阻抗得Cdm,c;将P3、P4短路,测量并拟合同时得到其他所有电感和电阻。其优点是可以直接测量,但不适于设计期间对相关参数的估算,也无法研究材料属性对这些参数的影响。
本文采用有限元计算的方法来确定这两个杂散电容,以克服上述阻抗测量法的不足。
设有 n匝的扼流圈(两线圈匝数均为 n/2,见图1),各线匝的序号分别为0,1,2,…,n-1(见图3),其中0线匝为参考线匝。通过建立该系统的静电场模型,可以计算得到任意两线匝(i线匝和j线匝)之间的部分电容Cij(i,j=1,2,…,n-1;i=j表示该匝对参考线匝的部分电容)[15]。此时,静电场特性转化为“电容”网络求解问题。因为扼流圈上下两部分线圈结构和电气完全对称,所以图2中的四个节点P1~P4分别与图 3 中的 n/2、(n/2+1)、1、0 序号匝对应,即利用静电场建立的电容二端口模型如图 4所示。

图3 扼流圈线匝排列Fig.3 Arranging of turns for choke

图4 二端口电容网络Fig.4 2-port network of capacitance
若图4二端口网络的导纳矩阵为Y

式中,Y各元素
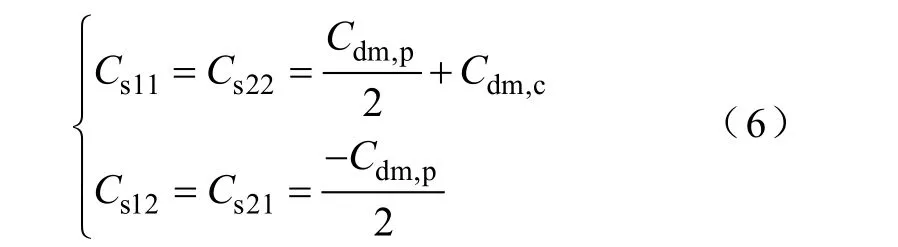
则图4电容网络中的电容为

因此,求解图 2网络中差模电容的关键在于求解式(5)的导纳矩阵或电容矩阵。
(1)求解Ys11及Cs11。根据导纳矩阵Y的定义,对图3和图4
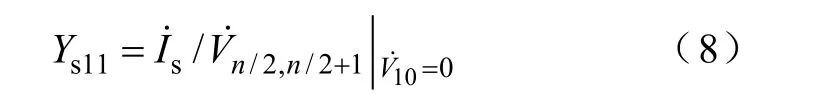
令s1I=˙,则

即将输出节点1与参考节点0之间短路,输入节点(n/2+1)与节点n/2间加单位电流Is=1(方向由后者指向前者),Ys11与输入节点电位之间关系为式(9)。
选择第0匝为参考节点,列节点电压方程


式中,Yc为式(10)左边电容矩阵划去第一行和第一列后的方阵。令

则方程(11)变为
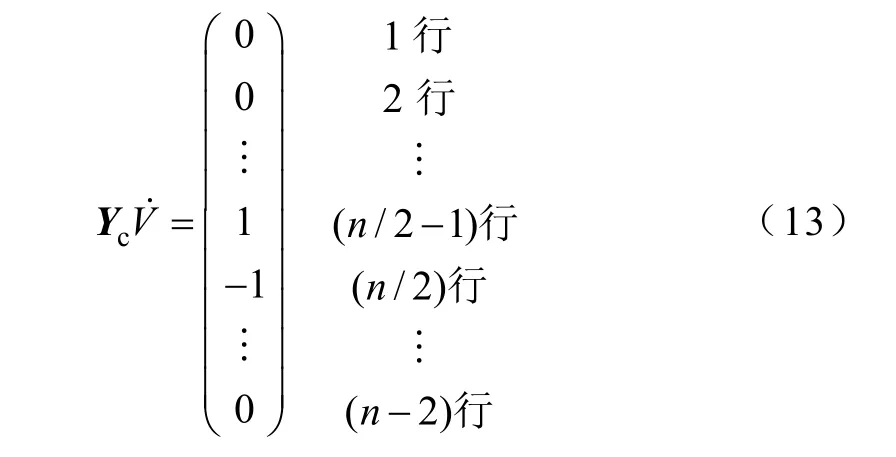
求解该方程,可得节点(n/2)、(n/2+1)对应的电位值

代入式(9),得
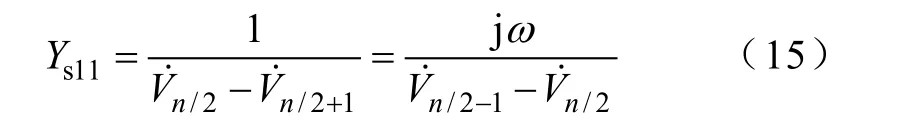
对应电容
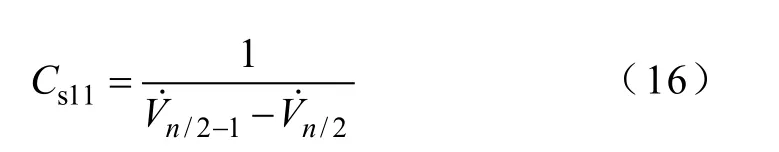
因此,只要形成式(11)中电容矩阵Yc以及形成方程式(13),求解该方程,得第(n/2-1)与(n/2)解的值,则“作差”然后求“倒数”即为等效电容Cs11的值。
(2)求解Ys12及Cs12。仍然采用图3和图4,导纳元素Ys21为

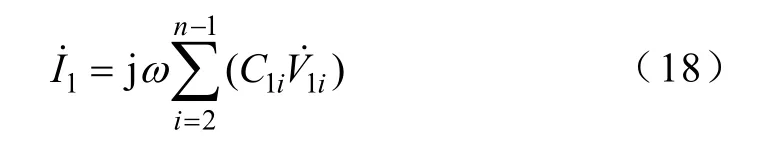
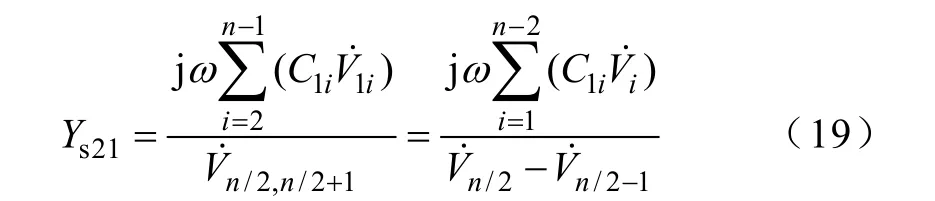
结合式(5),对应的等效电容
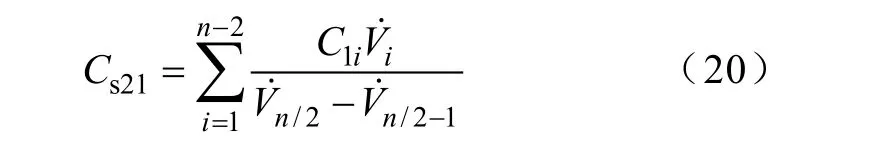
因此,同计算Cs11一样,形成的方程相同,求解过程也为同一个方程组,计算Cs21与Cs11只是计算式的分子不同,如式(20)和式(16)。
2.1.3 差模电感Ldm
对于图1的扼流圈,只要输出端短路,输入端加载一电压或电流,则此时由于两个输入端子的电流方向相反,所以扼流圈呈现出“差模”特点。即图2中P3、P4短接,则等效为图5采用电阻、电容和电感表示的并联电路。
若测定该扼流圈差模状态时的谐振角频率ωr,则等效阻抗或导纳虚部为零,即求解以L为变量的一元二次方程式(21),则可以求得差模电感Ldm。


图5 扼流圈呈“差模”状态Fig.5 Choke occurs at DM state
2.2 共模干扰信号二端口等效
扼流圈共模干扰信号是指输入端口或输出端口的两个端子电流相同(见图6)。由于扼流圈两部分线圈绕向相反,所以共模时磁心内的磁通获得增强,磁心等效电感和电阻比差模时大大提高,且二者均与加载电流频率紧密相关,这是由于铁氧体磁心内的涡流效应。

图6 扼流圈共模干扰信号Fig.6 CM noise signals of choke
将 P1、P2连接,P3、P4连接,P1(P2)、P3(P4)间加载电压,则扼流圈表示为“共模”特性。若扼流圈的总匝数为n,每线圈的匝数为n/2,则此时扼流圈相当于一个匝数为 n/2的电感器,每匝导线由两股导线并绕而成。
同差模模型一样,共模线圈线匝之间也存在杂散电容。考虑到扼流圈结构对称性和电流的同方向性,所以两线圈间无杂散电容效应,电容杂散效应仅存在于同一线圈内。简单近似分析,同一线圈内寄生电容基本与所有线匝间电容串联后相近,匝数愈多,则该电容值愈小,运行或测量时受环境影响愈大。因此,该寄生电容以实验的方法获得可以考虑周围环境的影响。
综上所述,扼流圈共模干扰信号的等效模型如图 7所示。其中电阻 Rcm=Rc+Rw,Rc为磁心等效交流电阻,可以采用类比有限元法计算[14];Rw为导线交流电阻,仍然可以采用式(1)~式(3)Rdm的公式计算,只是计算时匝数采用 n/2时,其值为采用式(1)计算的两个电阻并联结果。电感Lcm=Lc+Lw,其中Lc为磁心交流等效电感,采用类比有限元法计算[14];Lw为导线等效交流电感,一般远小于Lc,采用式(4)计算,匝数仍然为n/2,其值为采用式(4)计算的两个电感并联的结果。
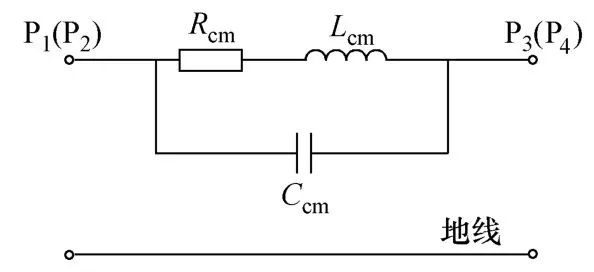
图7 扼流圈共模等效Fig.7 CM equivalent circuit for choke
图7共模等效阻抗的虚部为
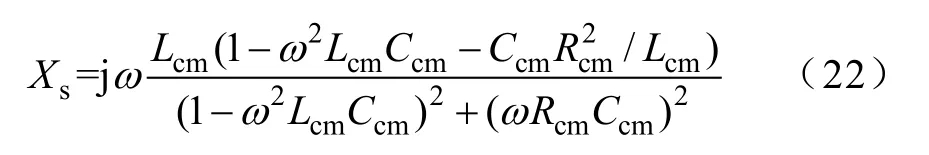
令Xs=0,则图7共模电路呈谐振状态。由于寄生电容Ccm与f无关,而Lcm=Lcm(f ),Rcm=Rcm(f ),所以
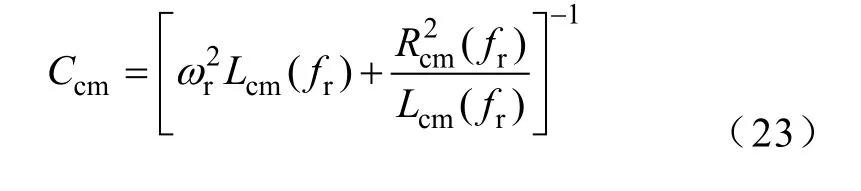
3 散射参数法测试扼流圈二端口导纳参数
3.1 扼流圈二端口网络及其导纳矩阵
如前所述,差、共模二端口网络可统一采用图8模型表示。该二端口的导纳矩阵Y为

若已知Yij(i,j=1,2),则
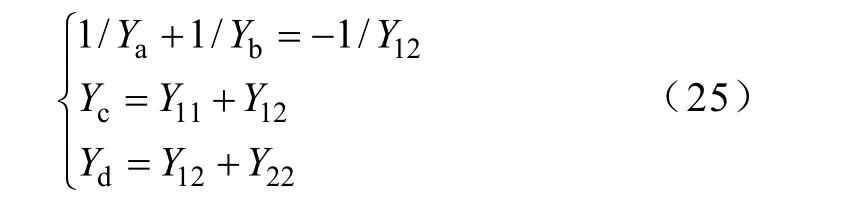
对差模二端口模型(见图2),Ya=Yb,则

对共模二端口模型(见图 7),1/Yb=0,Yc=Yd=0,则

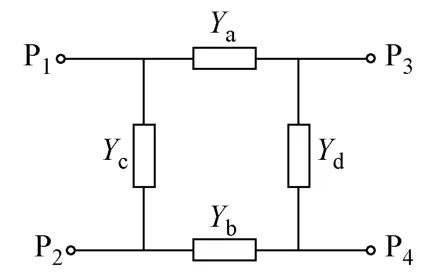
图8 扼流圈差、共模统一的二端口模型Fig.8 Uniform 2-port model on DM and CM for choke
3.2 散射参数测量导纳矩阵
如果能够以导纳或阻抗的方式描述扼流圈则可以更方便地进行系统设计和优化。扼流圈二端口网络的导纳、阻抗或转移参数可以通过直接测量的方法得到,但是这些参数的直接测量需要一端进行严格的“短路”或“开路”,对于要考虑的传导干扰达到30MHz这样的频率,严格的“短路”或“开路”是难以实现的。可以通过在二端口加载电压和电流信号,在两端分别阻抗匹配条件下,测试其散射参数的方法来进行二端口网络参数的间接测量。散射参数可表示为

该散射参数满足

采用散射参数S的显著优点是,测量时不需要对端口进行“开路”或“短路”,从而保证了测量精度。当测量得到散射参数式(28)时,则对应导纳矩阵Y的标幺值为[9]
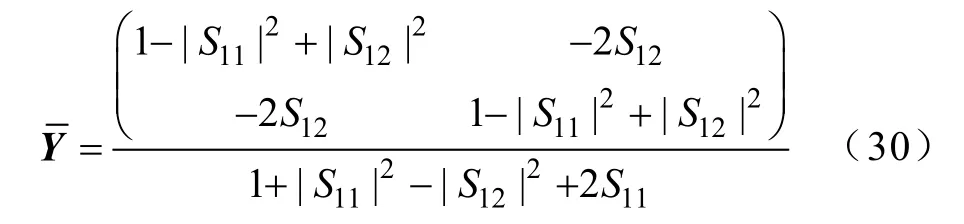
导纳矩阵

式中,Y01、Y02分别为测量传输线的特性阻抗,一般测量仪器为50Ω。
将式(31)中测量结果代入式(25)、式(26)或式(27)可以得到差、共模电路的二端口网络(见图8)各支路的导纳,与图2和图7对比,可以验证建立模型的正确性。
4 扼流圈二端口网络支路导纳(阻抗)计算和测量
本文以两个铁氧体扼流圈为例,其尺寸及相关参数结构见表1。
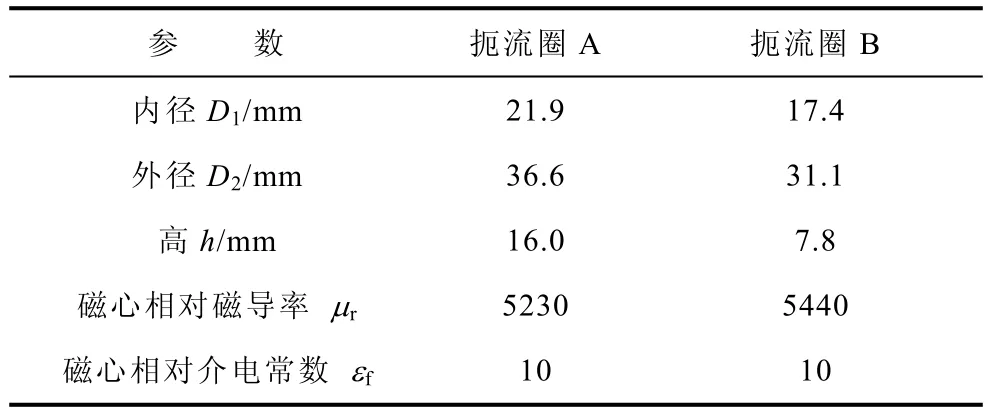
表1 模型扼流圈结构及材料参数Tab.1 Geometry and material parameters for 2 chokes
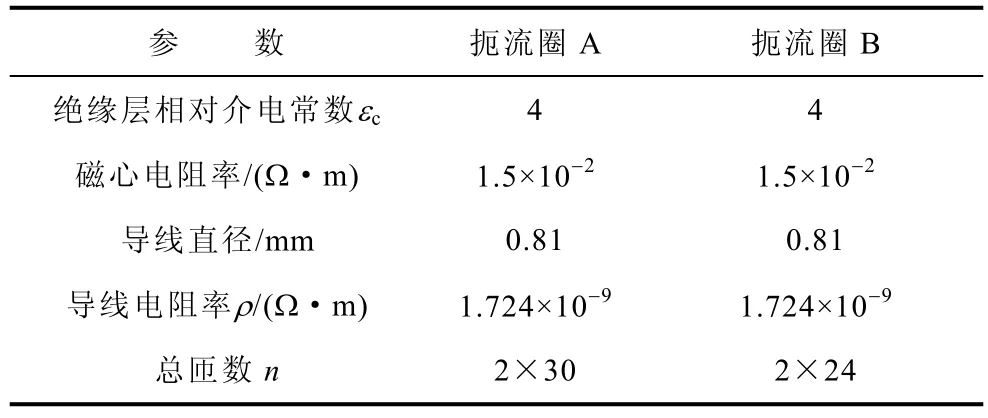
(续)
计算采用有限元软件ANSYS。采用的实验仪器为HP4284A—RLC测试仪和Agilent 4395A,前者可以测量20Hz~1MHz范围扼流圈的阻抗;后者不仅可以测量0.1Hz~500MHz范围的阻抗,而且可以测量扼流圈的散射S参数。
4.1 差模(DM)电路建立
在计算图4电容时,需要建立静电场模型计算任意两匝之间的部分电容Cij,采用式(7)、式(16)和式(20)可以计算出差模电路各支路的电容Cdm,p和Cdm,c。采用式(13)可以计算导线的等效交流电阻,近似为差模电阻 Rdm。测量得到的谐振频率为fr,求解方程(21)可以得到差模电感Ldm(见表 2)。

表2 DM电路计算及测量参数Tab.2 Parameters of DM circuit

图9 差模电阻频率特性Fig.9 Frequency properties of CM resistance
由此,可以得到差模电路时(见图8)的导纳为

因按导纳比较效果不明显,图 10比较了阻抗Za的幅值 za。比较显示,所建立的差模电路在传导电磁干扰30MHz范围有较好的适应性。
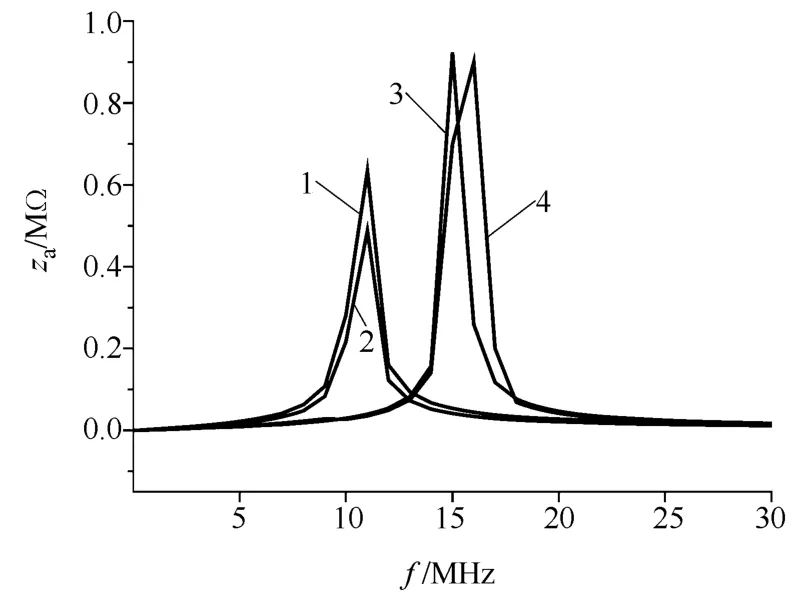
图10 差模电路支路阻抗计算与测量Fig.10 Calculating and measuring of branch impedance for DM circuit
4.2 共模(CM)电路的建立
对共模电路图7,利用2D时谐磁场有限元法,选择Plane 53或Plane 13单元可以类比求解得到磁心等效电阻 Rc和等效电感 Lc[14],其频率特性如图11、图12所示。导线计算公式类似差模电阻Rdm,只是共模时为两线圈电阻并联,差模为两线圈电阻串联。通过测量其谐振频率 fr,结合式(23)可共模寄生电容Ccm,具体数值见表3。
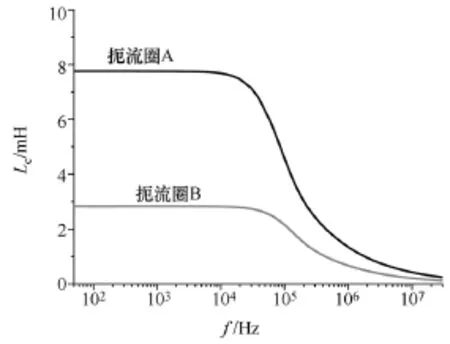
图11 共模电路磁心电感Fig.11 Core inductance of CM circuit

图12 共模电路磁心电阻Fig.12 Core resistance of CM circuit
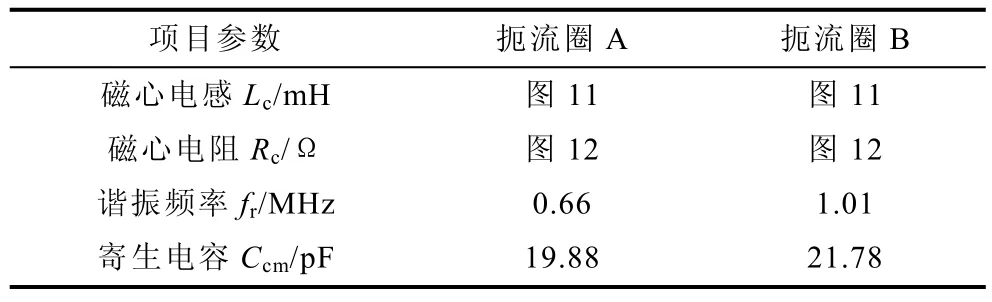
表3 共模电路计算参数Fig.3 Calculating parameters of CM circuit
对共模电路图7,对应图8的导纳
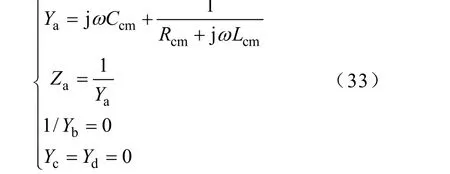
因此,只需对阻抗Za的幅值za进行计算和实验的比较,如图13所示。
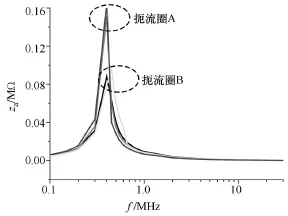
图13 共模电路支路阻抗za计算和测量Fig.13 Calculating and measuring of branch impedance za for CM circuit
同差模电路比较显示相似的结论,说明了在传导干扰30MHz的范围内,共模等效二端口等效电路具有一定的准确性。
5 结论
以铁氧体共模轭流圈为对象,分别建立了静电场和时谐磁场有限元模型,测量对应谐振频率,建立了扼流圈差模和共模二端口网络等效电路:
(1)扼流圈差模二端口网络模型中的电容可以通过有限元建立扼流圈的 3D静电场模型获得,且与频率无关;差模电感可认为仅由导线的交流电阻产生,随频率的增大而增大,数值一般为几欧姆;差模漏电感也可以认为与频率无关,数值较小。
(2)扼流圈共模二端口网络模型类似于一个独立的电感器,其等效为一个常数电容与另一条支路的并联,该支路由随频率增函数变化的电阻和随频率减函数变化的电感串联组成。
(3)通过测量散射参数的方法可以获得扼流圈等效各支路导纳或阻抗。因为测量只需入射端和反射端匹配即可,实施严格的“短路”和“开路”,所以测量精度较高。
(4)“有限元法+谐振频率法”建立的扼流圈二端口模型的各支路阻抗与散射参数测量结果基本一致,相互印证了建立模型方法的正确性和散射参数法测量的准确性。
[1]钱照明, 程肇基. 电力电子系统电磁兼容设计基础及干扰抑制技术[M]. 杭州: 浙江大学出版社, 2000.
[2]Wang Shuo. Characterization and cancellation of high-frequency parasitics for EMI filters and noise separators in power electronics applications[D].Blacksburg: Virginia Polytechnic Institute and State University, 2005.
[3]Wang Shuo, Fred C Lee, Willem Gerhardus Odendaal,et al. Improvement of EMI filter performance with parasitic coupling cancellation[J]. IEEE Trans. on Power Electronics, 2005, 20(5): 1221-1228.
[4]陈恒林, 陈玮, 冯利民, 等. 基于阻抗测量的共模扼流圈高频建模[J]. 电工技术学报, 2007, 22(4): 8-12.Chen Henglin, Chen Wei, Feng Limin, et al. High frequency modeling for common mode chokes based on impedance measurement[J]. Transactions of China Electrotechnical Society, 2007, 22(4): 8-12.
[5]Chen Wei, Feng Limin, Chen Henglin, et al. Analysis the inductance coupling effects on the differential mode EMI in power converter[C]. Applied Power Electronic Conference and Exposition, 21th Annual IEEE, 2006: 1169-1173.
[6]Marian K Kazimieczuk, Giuseppe Sancineto, Gabriele Grandi, et al. High-frequency small-signal model of ferrite core inductors[J]. IEEE Trans. on Magnetics,1999, 35(5): 4185-4191.
[7]Gabriele Grandi, Marian K Kazimieczuk, Antonio Massarini, et al. Model of laminated iron-core inductors for high frequencies[J]. IEEE Trans. on Magnetics, 2004, 40(4): 1839-1845.
[8]Bartoli M, Reatti A, Kazimierczuk M K. Highfrequency models of ferrite core inductors[C].IECON1994 20th International Conference on Industrial Electronic Control and Instrumentation, 1994, 3:1670-1675.
[9]毛钧杰. 微波技术与天线[M]. 北京: 科学出版社, 2008.
[10]Wang Shuo, Odendaal W G, Lee F C. Extraction of parasitic parameters of EMI filters using scattering parameters[C]. Industry Application Conference 2004,19th Annual Meeting, Conference Record of the 2004 IEEE, 2004, 1: 3-7.
[11]Wang Shuo, Fred C Lee, Willem Gerhardus Odendaal.Characterization and parasitic extraction of EMI filters using scattering parameters [J]. IEEE Trans. on Power Electrics, 2005, 20(2): 502-510.
[12]Reggiani U, Grandi G, Sancineto G, et al. Highfrequency behavior of laminated iron-core inductors for filtering applications[C]. APEC 2000, 15th Annual IEEE Applied Power Electronics Conference and Exposition, 2000, 2: 654-660.
[13]Shuo Wang, Fred Lee, Odendaal W G. Single layer iron powder core inductor model and its effect on boost PFC EMI noise[C]. 34th Power Electronics Specialists Conference, 2003, 2: 847-852.
[14]王世山, 黄诗友, 谢少军. 类比有限元法求解铁氧体电感器磁场特征参数[J]. 中国电机工程学报,2009, 29(6): 122-128.Wang Shishan, Huang Shiyou, Xie Shaojun. Solution of magnetic characteristic parameters by using analogizing finite element method for ferrite core inductor[J]. Proceedings of the CSEE, 2009, 29(6):122-128.
[15]王世山, 崔永生, 谢少军. 铁氧体环形电感器寄生电容的提取[J]. 电工技术学报, 2009, 24(4): 22-29.Wang Shishan, Cui Yongsheng, Xie Shaojun.Extraction of parasitic capacitance for toroidal ferrite core inductor [J]. Transactions of China Electrotechnical Society, 2009, 24(4): 22-29.

