某边坡稳定性评价中块体理论的应用

游 萍,林晓强,况磊强

(1.四川电力职业技术学院,成都,610072;2.贵州桐梓河水电开发有限公司,贵州遵义,5630002;3.四川大学水利水电学院,成都,610065)

1 前言

岩体是一种复杂的地质体,通常认为由岩块和结构面两部分组成。结构面如节理、断层、岩层层面、剪切带、软弱夹层等;岩块则是被结构面切割后形成的不同大小的岩石块体,岩块内物质相对连续致密。结构面发育可能存在很大的差异,岩体变形失稳往往是由于结构面发生张开、闭合、错动而引起的,因此,结构面的存在及其强度,控制着岩体的强度及稳定性。

1985年GoodmanR E与石根华正式提出块体理论(Block Theory)[1～2]。其基本假设为:(1)结构面为平面并贯穿研究的岩体;(2)结构体为刚体,不考虑岩体的变形;(3)岩体破坏沿结构面产生剪切滑移。其核心是寻找关键滑移块体。由于结构面的组合是随机的,则由结构面切割而成的岩石块体为随机块体。在边坡开挖面处,随机块体有可能成为关键滑移块体。

随机块体主要是指由地质勘探阶段位置不能确定的裂隙或裂隙面与岩体开挖面切割形成的块体。随机块体研究方法是根据裂隙产状及开挖临空面的方位,利用块体理论搜索在多组裂隙切割条件下,岩体开挖面上各类关键块体的类型,分析块体几何特征及其稳定性。可移动块体的判断准则为:若节理锥完全落于某边坡开挖面或交角的空间锥内,则该节理锥为相应的可移动块体,且当节理锥的剩余滑动力为正(即滑动力大于阻滑力),则该节理锥相应的块体为关键块体。目前,块体理论已在我国被广泛应用[3～9]。

2 工程概述

某水电站泄水建筑物由泄洪洞和放空洞组成,其放空洞进口位于一凹腔陡崖之上,下游侧紧邻泄洪洞进口,整个坡段全长100m,边坡总体呈上缓下陡,在约1630m高程以下为陡崖,坡度约为65°～70°,之上自然坡度35°～50°,自然边坡高度500m～700m。放空洞纵轴线方向S11.4°W,纵剖面呈台阶状地形,在1590m和1700m高程左右均有一缓坡平台,其上下陡坎坡度65°～70°。放空洞进口开挖坡高约140m,洞脸边坡走向为N78°33′03″W,开挖坡比1∶0.5。

该放空洞进口边坡岩体裂隙比较发育,由于裂隙面和结构面的组合切割,使岩体被切割成不连续的块体。

坡体内主要出露澄江～晋宁期花岗闪长岩(δ02(3))和中粗粒花岗岩(γ2(4)),其下部公路边侵入少量细晶花岗岩脉(γl),洞口一带基岩直接裸露。

坡体中主要结构面有J4、J7、J2、J6四组,此外,还零星发育延伸较短小的J9组裂隙。岩体结构总体为块状结构,局部次块状。放空洞进口段裂隙发育统计情况见表1。

表1 放空洞进口裂隙发育统计和计算参数取值

3 节理组合

此边坡岩体的结构面发育具有明显的不均衡性,其主要发育有J4、J7、J2和J6四组节理。因此,可能出现某3组或4组节理面(加临空面)切割而成的块体。为了找出各临空面上的可移动块体,根据地质资料和调研分析,分别按不同危险节理组合(表2)计算分析搜索最大关键块体,分析其稳定性。

表2 随机块体分析中的不同节理组合

4 关键块体搜索

对不同节理组合进行下极点全空间赤平投影,分析可移动块体的类型。然后根据块体的剩余滑动力大小,初步判断该可移动块体是否为力学可移即关键块体。采用石根华博士的关键块体搜索程序SRM,搜寻边坡的最大关键块体,并计算各最大关键块体的滑动力系数和安全系数。

4.1 J4、J7和J2组合

根据关键块体搜索程序SRM,搜寻出由J4、J7和J2三组节理形成的最大关键块体,其滑动力系数和安全系数见图1和图2。最大关键块体只有001(其形状见图3),由J4和J7构成滑动面。其滑动力系数为0.70,安全系数为0.26,体积为50.48m3,滑动力为900.36kN(岩体容重取2.60×103kg/m3)。块体在坡面出露面积为54.48m2,平均深度0.93m,小于设计锚杆长度6m～9m;按施工设计的3.0m×3.0m锚杆布置(锚杆深度6m～9m),平均每块出露块体约布置6根锚杆,每根锚杆平均受力148.74kN,在锚杆受力范围之内。图1中,“110”等为节理锥的编号。

图1 边坡最大关键块体位置及滑动力系数分布(J4、J7和J2组合)

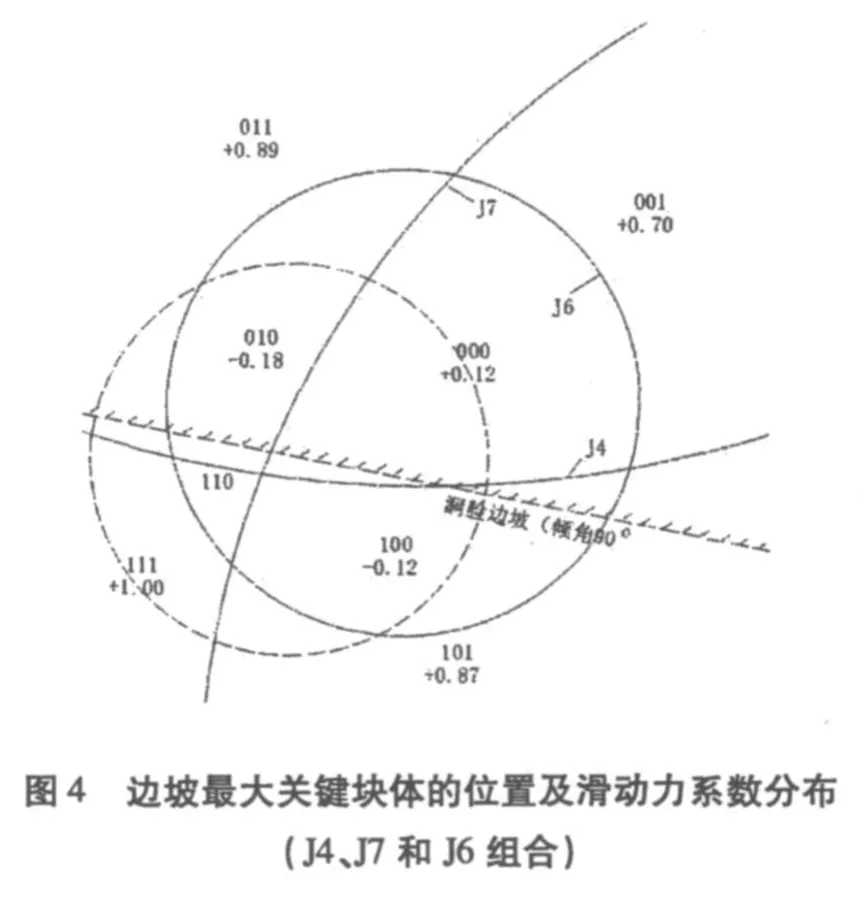
4.2 J4、J7和J6组合

根据关键块体搜索程序SRM,搜寻出由J4、J7和J6三组节理形成的最大关键块体,其滑动力系数和安全系数见图4和图5。只找到最大关键块体001,其形状见图6,由J4和J7构成滑动面。其滑动力系数为0.70,安全系数为0.26,体积为67.59m3,滑动力为1205.54kN,块体在坡面出露面积为75.29m2,平均深度0.90m,小于设计锚杆长度6m～9m;每根锚杆平均受力144.11kN。

4.3 J4、J7、J2和J6组合

洞脸边坡以上开挖边坡方向为N78°33′03″W,开挖坡比1∶0.5。计算取值为:倾向11.5°,倾角63°。根据关键块体搜索程序SRM,搜寻出由J4、J7、J2和J6四组节理形成的最大关键块体,其滑动力系数和安全系数见图7和图8。最大关键块体只有0010这一块,其形状见图10,由J2和J6构成滑动面。其滑动力系数为0.09,安全系数为0.82,体积为37.33m3,滑动力为85.61kN,块体在坡面出露面积为27.54m2,平均深度1.36m,小于设计锚杆长度6m～9m;按施工设计的3.0m×3.0m锚杆布置(锚杆深度6m～9m),平均每块出露块体约布置3根锚杆,每根锚杆平均受力27.98kN。

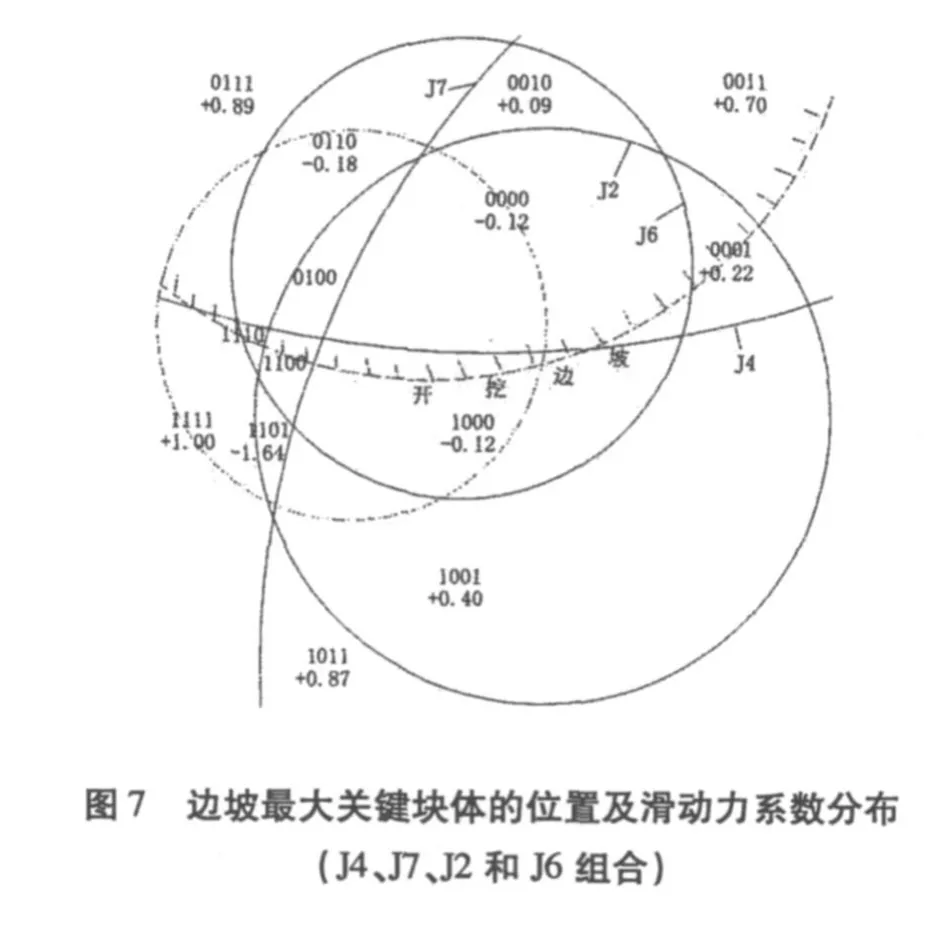
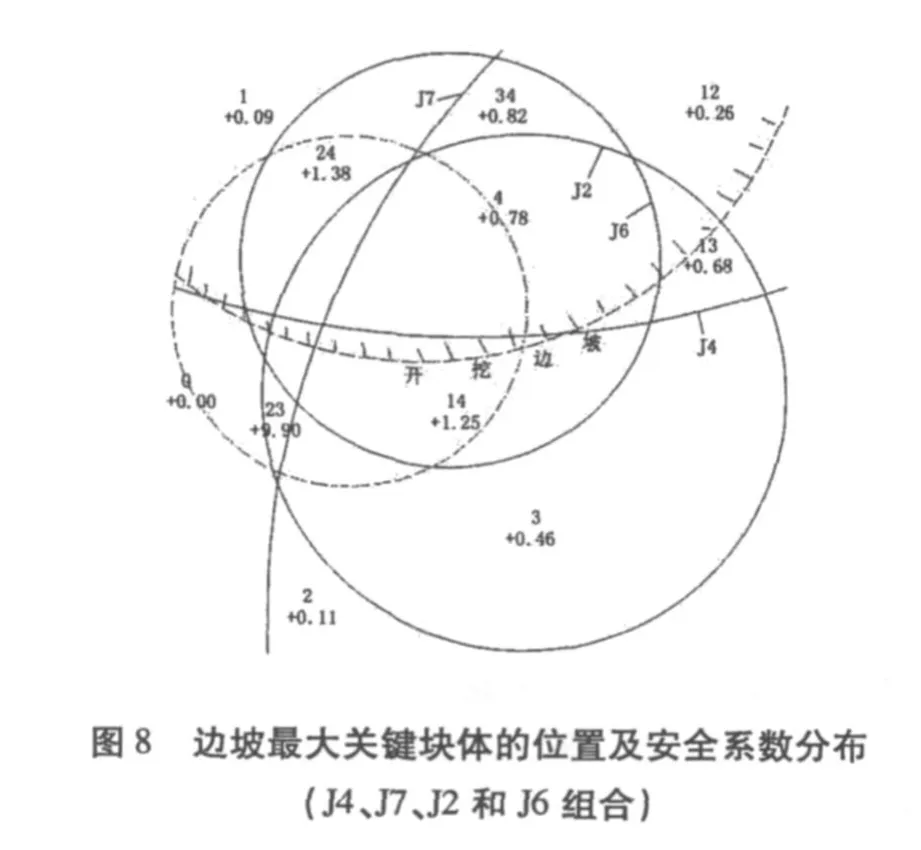
图9 边坡最大关键块体0010形状示意(J4、J7、J2和J6组合)

4.4 J4、J7、J2和J9组合

根据关键块体搜索程序SRM,搜寻出由J4、J7、J2和J9四组节理形成的最大关键块体,其滑动力系数和安全系数见图10和图11。找到最大关键块体0000和0010,其安全系数各为1.93和1.76,均不可动,所以在J4、J7、J2和J9组合下右岸放空洞进口边坡以上没有可动的关键块体。

表3给出了上述分析的综合结果。经分析可知,此边坡在各种危险节理组合情况下形成的块体条件较好,关键块体在坡面的出露面积相对较大,平均深度为1m～1.5m左右,小于锚杆的设计长度6m～9m,且锚杆受力最大约150kN,均在锚杆受力范围之内,能达到稳定要求。

表3 边坡最大关键块体汇总

5 结论

应用块体理论赤平解析法分析某水电站放空洞进口边坡的稳定性,可以得到如下结论:

5.1 从块体理论分析结果来看,此边坡稳定性总体情况较好,只是由于结构面切割在局部可形成不稳定块体,局部块体的稳定性主要受控于J4、J7两组陡倾角裂隙,需密切关注J4、J7的发育情况。

5.2 块体理论是裂隙岩体稳定性识别、分析的有效方法,一定程度上弥补了连续介质理论的局限性。

5.3 块体理论通过关键块搜索,可明确不稳定块体的几何特征与稳定性。放空洞进口边坡小断层和挤压破碎带较发育,其产状对上游侧边坡稳定不利,应加强锚固措施;在下游侧边坡岩体中,不存在控制边坡稳定的软弱结构面。因此,工程边坡在开挖过程中,应采取相应的支护措施。

〔1〕Shi Genhua,Goodman R E.Block Theory and Its App lication to Rock Engineering[M].New York:Prentice Hall,1985.

〔2〕Shi G H,Goodman R E.The Key Blocks of Unrolled Joint Traces in Developed Maps of Tunnel Walls[J].international Journal for Numerical and Analytical Methods in Geomechanics.1989,(13):131～158.

〔3〕刘锦华,吕祖珩.块体理论在工程岩体稳定分析中的应用[M].北京:水利电力出版社,1988.

〔4〕邬爱清,张奇华.岩石块体理论中三维随机块体几何搜索[J].水利学报,2005,36(4).

〔5〕张奇华,邬爱清,石根华.关键块体理论在百色水利枢纽地下厂房岩体稳定性分析中的应用[J].岩石力学与工程学报,2004,23(15):2609～2614.

〔6〕毛海和,夏才初,张子新.块体理论赤平解析法在龙滩水电站地下厂房洞室群稳定分析中的应用[J].岩石力学与工程学报,2005,24(8):1308～1314.

〔7〕卢 波,陈剑平,王良奎.基于三维网络模拟基础的复杂有限块体的自动搜索及其空间几何形态的判定[J].岩石力学与工程学报,2002,21(1):62～64.

〔8〕黄正加,邬爱清,盛 谦.块体理论在三峡工程中的应用[J].岩石力学与工程学报,2001,20(5):648～652.

〔9〕张子新,孙 钧.块体理论赤平解析法及其在硐室稳定分析中的应用[J].岩石力学与工程学报,2002,21(6):1556～1560.