干涉仪测向中相关处理算法的研究
王 磊,束 坤
(1.江苏科技大学,镇江212003;2.船舶重工集团公司723所,扬州 225001))
0 引 言
相位干涉仪测向体制具有测向精度高、算法简单、实时性好等优点。为了进一步提高测向精度和抗多径能力,干涉仪测向设备一般要使用大于半波长的基线,此时测量的相位差会出现多值,即相位差模糊。虽然可以采用长短基线结合的方法解决相位差模糊问题,但这不仅使算法更加复杂,而且设备量将会随测向精度的提高而大大增加。
相关处理算法应用于干涉仪测向体制后,使干涉仪测向体制不再受半波长的约束,提高了测向精度,解决了相位差模糊与提高测向精度之间的矛盾。
1 干涉仪测向体制的基本原理
干涉仪测向的实质就是通过测量空间来波信号在接收天线上形成的相位差后确定空间来波信号的到达角。以2个天线单元阵为例(见图1),介绍干涉仪测向体制的基本原理。

图1 干涉仪测向原理图
图1中d为天线1与天线2之间的基线长,θ为入射波的到达角度,则相位差为:

式中:λ为入射波波长。
所以知道相位差后就可求出入射波到达角度:
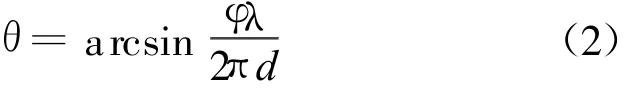
在式(1)中,当d≥λ/2时 ,φ的取值会超出[-π,+π]的范围。相位差 φ是由鉴相器测得的,而鉴相器的输出范围只能在[-π,+π]之内,是以2π为周期的,所以在d≥λ/2时相位差会出现相位差模糊,随之带来的就是更多的测向模糊。
针对上述情况,可以得到以下2种解决相位差模糊的方法:
(1)采用较小口径的天线阵,d<λ/2;
(2)采用长短基线相结合的测向体制。
下面分析干涉仪测向体制的测向误差。对式(1)求全微分,可得:

整理上式,用增量表示,可得:
忽略掉天线基线d变化造成的误差,通常频率变化误差也可忽略,则测向误差可表示成:

由上式可知:
(1)测向误差主要是由测量的相位差误差引起的;
(2)当 θ=0°时 ,测向误差最小;当 θ=90°时,测向误差最大,此时干涉仪已经失去了测向功能;
(3)基线长度d越长,测向误差越小,测向精度越高。
综上可知,在传统的干涉仪测向中,d<λ/2可消除相位差模糊,但测向精度很不理想,当增大基线长度d后,虽然可提高测向精度,但相位差模糊就无法消除了。这就是消除相位差模糊和提高测向精度之间的矛盾。
2 相关干涉仪
为了解决相位差模糊与测向精度之间的矛盾,可以在干涉仪测向中采用相关处理算法,即用相关干涉仪解决此矛盾。相关干涉仪测向技术是在干涉仪测向技术的基础上发展而成的,它是通过比较获取的入射波相位差与事先已存的各方位入射波相位差的相关性来得到入射波方向的。以多单元均匀圆阵为例,在多单元圆阵中,选取若干个天线对,对于一个确定入射角的入射信号,从这些天线对可以测得相应的相位差,这些相位差值由天线阵的结构决定。由已知的天线阵结构可以通过理论计算得出相位差值,也可以通过实际测量得出。在360°全方位上,每隔一固定的间隔选取一个方向ωi(i=1,2,…,n),每一个方向有若干个天线对的相位差值φj(j=1,2,…,m)相对应,m为选取的天线对数量。由这些天线对得到的相位差值称为相关干涉仪测向体制的原始相位样本。当一个实际的入射信号入射到天线阵上时,系统测量出一组相位差,然后将这一组值和系统原始相位样本进行相关处理,可得出它们的相关系数,相关系数的最大值对应的角度就是入射信号的到达角度。
下面以五单元均匀圆阵为例来具体分析相关处理算法。五单元均匀圆阵如图2所示。

图2 五单元均匀圆阵原理图
5个天线的位置如图所示,由5个天线形成的5条基线为基线1-3、基线2-4、基线3-5、基线4-1、基线5-2,长度均为d,建立如图所示坐标,基线5-2与x轴重叠,y轴穿过天线1,基线5-2的法线平行与y轴,θ为入射波方向,λ为入射波波长,则基线5-2对应的相位差为:

以此类推可得其它4条基线对应的相位差为:

在360°的方向上以5°为间隔可取到73个方向ωi(i=1,2,…,73),方向 ωi对应的相位差为 φi=为第 i 个方向上基线5-2上的相位差),设实际入射信号方向为50°,则此方向上的相位差可求得为分别为实际来波方向上对应5条基线上的相位差,可得 Ψ和φi的相关系数为:

式中 :Cov(Ψ,φi)为 Ψ和φi的协方差 ;D(Ψ)和D(φi)分别为 Ψ和φi的方差,取基线长度与入射波波长之比为1/2,图3为对此算法仿真的结果。

图3 d/λ=1/2时的相关图
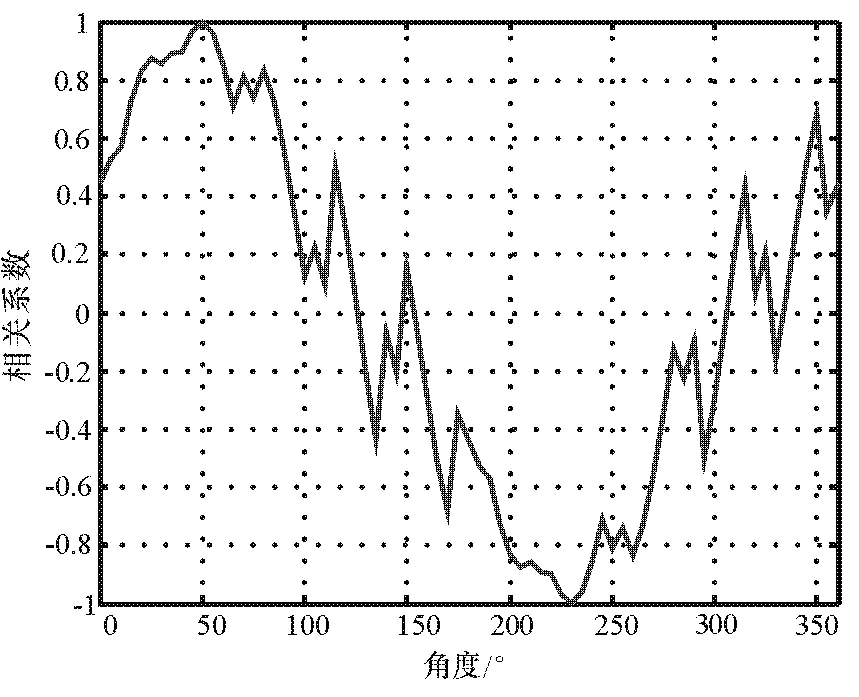
图4 d/λ=3/2时的相关图
由图 3可知,在 50°处的相关系数为 1,即 50°方向有入射信号,但此图中入射信号方向处过于平滑,测向精度不高。图3在与50°方向相差约180°的230°方向上的相关系数为-1,这是因为50°方向上的相位差与此方向上的原始相位样本大小相等,方向相反,形成了负相关。由上面分析可知,增大基线长度可提高测向精度,如图4所示,在50°方向上有比较尖锐的峰,测向精度被提高。
3 其它两种处理算法的研究
下面介绍的两种算法的仿真结果都是在上一节给出的五单元均匀圆阵下实现的。
第一种处理算法是基于最小二乘估计的,它不是求实际入射信号的相位差与原始相位差的相关系数,而是通过求对应基线上实际入射信号的相位差与原始相位差的误差平方和最小值来确定入射信号方向的,代价函数如下式:

式中:j=1,2,…,5;i=1,2,…,73;Ψj为实际入射信号第j个基线上的相位差;φji为第j个基线在第i个方向上的原始相位差。
使αi最小的即为实际入射信号的到达角度。
由图5和图6可知,最小值在 50°处,所以入射信号角度为50°,且增大天线口径后,图6中50°处图形较尖锐,由此可知此处理算法在基线长大于半波长时测向精度得到了提高且无测向模糊。
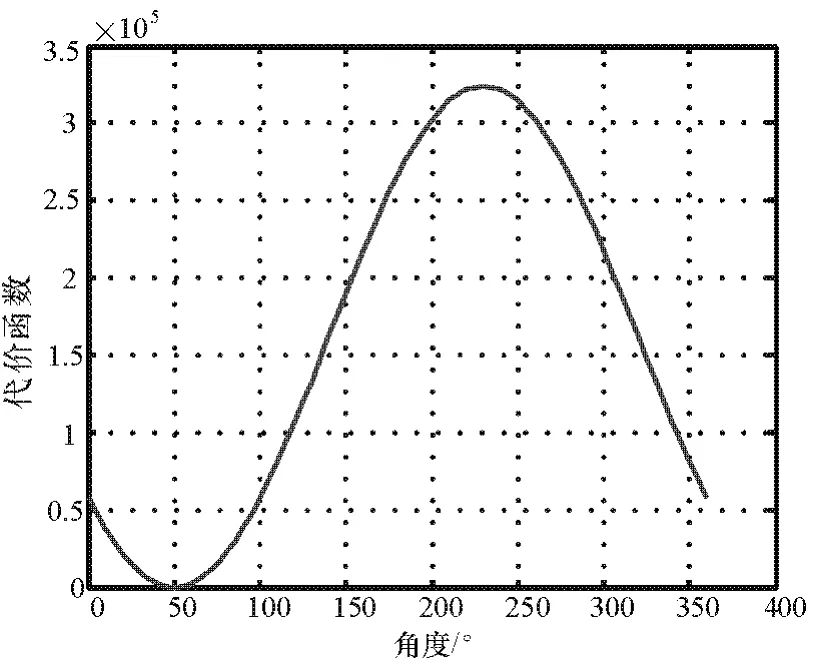
图5 d/λ=1/2时的相关图

图6 d/λ=3/2时的相关图
第二种处理算法可以避免鉴相时的三角运算,把代价函数的运算从复数域简化到实数域,减小了运算量,把原始相位的余弦 cosφji和正弦 sinφji与实际测得入射信号的余弦cosΨj和正弦sinΨj作相关运算后再把相关运算得到的值作归一化处理,如下:

式中:max(βi)为 βi的最大值 。
仿真结果如图7~8所示。

图7 d/λ=1/2时的相关图
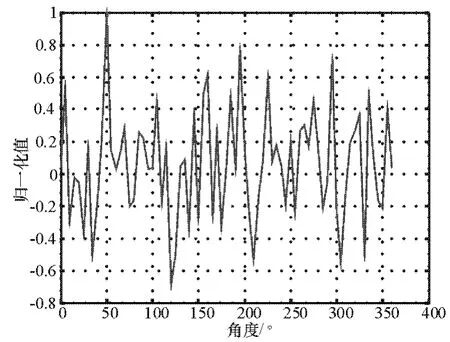
图8 d/λ=3/2时的相关图
由图7可知,当d/λ=1/2时此处理方法的精度已明显好于前面提到的处理算法,从图8可以知道,当增大天线口径后,相比较于图7,测向精度却没有明显变化,但其本身精度已经明显高于前面算法的精度了。
4 结论
相关处理算法是相关干涉仪设计中重要的一项,它能够在保证不出现相位差模糊的情况下使用大口径天线来提高测向精度与抗干扰能力,对入射波的波前失真也有一定的抑制作用。现代的数字信号处理技术可以使相关处理算法更加易于实现,只需存储采集到的原始相位样本后,把实际的入射波相位差与已经存储的原始相位样本进行相关匹配处理即可。当原始相位差样本通过实际测量得出时,那么原始相位差样本就包含了系统的固有偏差、设备制造误差和入射信号的所有相位信息,所以设备本身能够达到很高的精度。
[1]赵国庆.雷达对抗原理[M].西安:西安电子科技大学出版社,1999.
[2]杜龙先.单信道相关干涉仪测向原理[J].中国无线电管理,2000,2(1):41-42.
[3]An Xiaobo,Feng Zhenghe.A signal channel correlative direction finder using VXI receiver[J].International Conference on Microwave and Millimeter Technology Proceedings,2002(3):1158-1162.
[4]赵树杰,赵建勋.信号检测与估计理论[M].北京:清华大学出版社,2005.
[5]李淳,廖桂生,李艳斌.改进的相关干涉仪测向处理方法[J].西安电子科技大学学报(自然科学报),2006,33(3):400-403.

