智能集成运动控制系统研究

董玮

（东软信息学院计算机系，辽宁 大连 116023）

1 引言

智能控制技术是当代新技术革命的核心，尤其在工业应用领域，诸如智能生产系统、计算机集成制造系统、智能机器人系统等高新技术得到了广泛的应用。工业应用中主要的智能控制方法有模糊控制、神经网络控制、学习控制、专家系统等［1］。但是，每种方法都有各自的优缺点，单一的智能控制方案有时并不能达到满意的控制效果，因此，在某些特定的控制场合，需要将几种不同的智能控制方法甚至非智能控制方法结合起来使用，这就是所谓的智能集成控制。

本文从提高系统的跟踪精度出发，研究了智能集成控制在运动控制系统中的一些应用，实验结果表明，采用智能集成化的方法，系统可以自动辨识被控对象参数并选择控制方案、调整控制器参数以达到控制要求。

2 智能集成运动控制系统

2.1 智能集成运动控制系统的结构

智能集成控制系统能够根据被控对象的特性以及控制的要求自动地选择控制方案及控制器参数，系统的结构如图1所示。

图1 智能集成运动控制系统结构图

图1中，人机界面部分负责与用户的对话，允许用户输入所要求的性能指标以及跟踪信号的有关信息，并在线地显示选择的控制方案、控制器参数以及输出的性能指标；参数辨识系统可以根据系统的阶跃响应实时地辨识有关参数，与用户的要求一起提供给专家策略库和参数调整系统；专家策略库负责选择可能满足用户要求的控制策略或者控制方案；参数调整系统根据控制策略以及用户的要求选择控制器的参数；性能指标检测部分实时地检测系统的相关性能指标，显示给用户，同时反馈给专家策略库和参数调整系统，以便于系统决定是否需要进一步调整控制器的参数或者更改控制策略。

2.2 智能集成运动控制系统的工作流程

智能集成运动控制系统的工作流程如图2所示。

图2 智能集成运动控制系统流程图

（1）输入控制指标

由人机界面部分完成，由用户输入包括时域控制性能指标（例如上升时间、超调量、稳定时间、稳定精度等）、给定信号（例如信号类型及幅值、频率等）等有关信息。

（2）辨识被控对象

由参数辨识系统完成，辨识时可将被控对象近似等效为一阶惯性带延迟环节［1］，输入阶跃给定，从被控对象的输出响应根据Cohn-Coon公式提取被控对象特征参数。

（3）选择控制方案

由专家策略库实现。专家策略库中，存放着针对不同的输入及控制要求的控制方案，例如常用的PIDF控制、二自由度PID控制、自学习控制、零相位跟踪控制等，提供给系统选择。根据不同的要求，选择的控制方案可能是一种，也可能是几种方案的集成。

（4）调整控制器的参数

由参数调整系统完成，不同的控制器的参数自调整方案参见上述内容。

（5）实验结果

实验结果未必符合控制要求，这时，系统先调整控制器参数n次，若仍不能满足要求，则重新选择控制方案，再调整参数。控制方案共选择N次，仍不能满足控制要求的话则返回失败信息，表示控制要求与实际可以达到的要求不吻合，需要降低控制要求。

3 几种控制方案的比较

在专家策略库里，可供选择的控制方案有PIDF控制、二自由度PID控制、零相位跟踪控制、自学习控制等4种。控制方案的选择要遵循“首选优，后集成”的原则，即在所有的控制方案中，根据不同的控制对象、给定信号和控制要求，首先选择有可能最适合的控制方案并进行参数调整，不能满足要求时再选择其他有可能满足控制要求的方案，仍不能满足要求时，最后采用集成控制方案。控制方案的合理选择有赖于对不同的控制方案的深入研究，了解它们各自的优缺点及针对的控制要求，如表1所示为以上几种控制方案的比较，它提供了专家策略库选择控制方案的依据。

表1 不同控制方案的比较

4 智能集成运动控制系统的稳定性分析

智能集成运动控制系统用于工业现场，突出的问题就是能否保证连续生产中系统的稳定性。由于进行集成控制时，控制系统中的控制器参数甚至控制系统的结构都有可能发生变化，所以一定要保证系统参数或结构变化时不会对生产加工造成不利的影响，这样才能具有实际的应用价值。

由于这里所研究的都是闭环控制系统，因此可以将智能集成运动控制系统的控制部分简化为图3的形式，其中虚线框表示为可提供方案选择的控制策略库，r为输入位置给定，e为跟踪误差，u为控制量，y为系统输出。

图3 智能集成运动控制器结构简图

由图3可以看出，控制策略库的输入为系统的跟踪误差e，输出u作为被控对象的控制量，因此，要保证系统稳定，必须满足以下两个条件：①智能集成控制系统中每个控制器的设计都满足稳定性条件；②控制方案切换时要保证e-e·相平面上的曲线尽可能连续或者在允许的范围内有一定的跳变，即系统的参数或结构改变时，改变前的系统?作为改变后的控制初值。

5 智能集成运动控制系统实例

下面给出智能集成运动控制系统的研究实例，以展示智能集成控制的决策过程。

给定幅值为10000Pulse，周期为1s的正弦输入信号，要求跟踪误差不超过5%（即500Pulse），稳态误差不超过5‰（即50Pulse）。

图4 采用预测自学习控制的相平面曲线

由于输入是周期性信号，由表1可知，自学习控制和零相位跟踪控制都比较适合，但自学习控制的控制效果更加好。因此，系统首先选择预测自学习控制方案，得到的?相平面上的曲线如图4所示。实验误差曲线如图5所示，其中图5（a）为带过渡过程的误差曲线，（b）为稳态时的误差曲线。可以看出，稳态误差基本符合要求，但最大跟踪误差远远超出要求，因此，不符合控制要求，经参数调整后仍不能满足，因此，系统需重新选择控制方案。

图5 采用预测自学习控制的位置误差曲线

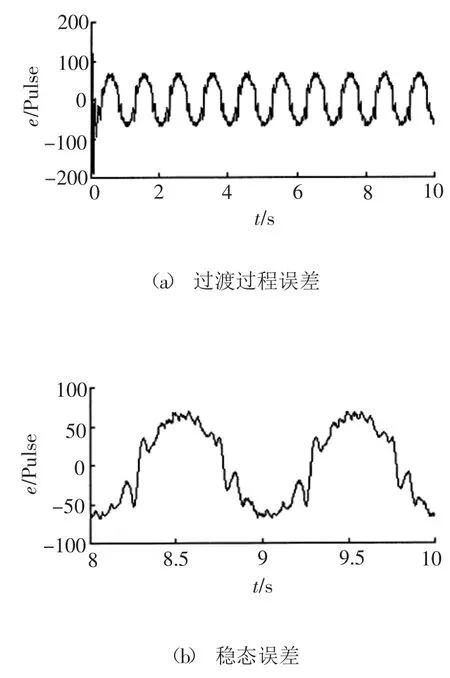
图6 采用零相位跟踪控制位置误差曲线

系统又选择零相位跟踪控制，其误差曲线如图6所示，此时得到的?相平面上的曲线如图7所示。最大跟踪误差符合要求，但稳态误差偏大，调整控制器参数后仍无法满足要求。

图7 采用零相位跟踪控制的相平面曲线

图8 采用智能集成控制的相平面曲线

图9 采用智能集成控制的位置误差曲线

这时，系统采用集成控制方案，将预测自学习控制和零相位跟踪控制结合起来，在第一个给定信号周期时，采用零相位跟踪控制，并将控制量与跟踪误差作为预测自学习控制的计算初值，从第二个给定信号周期之后，切换至预测自学习控制。此时?相平面上的曲线如图8所示，由于控制方法的切换，在切换点出现了曲线的跳变，但在允许范围内，不会对系统的稳定性造成不利的影响。实验误差曲线结果如图9所示，显然符合控制要求，因此，控制成功。

由这个实例可以看出，采用将多种控制方案结合起来的智能集成控制，再配以自动选择控制器参数以满足控制要求的功能，在运动控制系统中，将能够实现更高性能的控制要求。

6 结论

本文主要介绍了智能集成运动控制系统的分析、设计思路及具体的应用实例，这种将智能控制方案与非智能控制方案结合起来，并且自动进行系统辨识、根据用户要求选择控制方案和控制器参数的控制系统，将大大简化工业现场工程技术人员的控制器的参数调整工作，有着较高的实用价值。

［1］秦 忆，周永鹏，邓忠华等.现代交流伺服系统［M］.武汉：华中理工大学出版社，1995.

［2］DONG Wei,QIN Yi.Study on the Simulation of Servo-System Based on Two-Degree-of Freedom PID Control［J］.Advances in Systems Science and Application,2000，（1）：88-91.

［3］Tomizuka M.Zero Phase Error Tracking Algorithm for Digital Control［J］.ASME Journal of Dynamic Systems,Measurement and Control,1987,109（3）:65-68.

［4］李叶松，董 玮，秦 忆.运动控制系统自学习问题研究［J］.华中科技大学学报，2001，29（1）：66-69.