基于指数恢复模型的晶闸管阻容吸收参数设计
郝 勇 刘云霞 曾继伦
(1.国网电力科学研究院,南京 210003;2.南京规划设计研究院有限责任公司,南京 210096)
1 引言
随着高电压、大电流的晶闸管元件被广泛应用,晶闸管的反向恢复过电压问题受到了越来越多的关注,对阻容吸收电路的设计也提出了更高要求。众所周知,影响晶闸管反向恢复过电压的因素是多方面的,过电压的大小难以精确计算,如果阻容吸收的参数设计不当,往往难以达到最佳的吸收效果。这种过电压不仅会直接导致元件击穿,还会威胁到邻近设备的绝缘,对于这一问题应给予足够的重视。
目前,晶闸管阻容吸收电路参数的设计方法主要有两种:
第一种方法是采用电力电子设计手册中提供的经验公式[1],进行吸收电路的参数设计。其优点是计算简单,使用方便;缺点是缺乏针对性,难以达到最佳的吸收效果。
第二种方法是假设晶闸管在反向恢复电流峰值处突然完全截止,然后求解等值电路的微分方程,来确定最佳的阻容参数[2]。其优点是便于数学求解分析;缺点是假设条件带来的计算误差较大,这种假设不符合实际的物理过程,晶闸管的反向恢复电流不会突然截止,而是有一个连续的恢复过程。因此有必要改进这种设计方法。
近年来,国外提出了利用指数函数来模拟反向恢复电流的方法[3-5]。这种指数恢复模型有效克服了以上两种方法的不足,更符合反向恢复的实际物理过程。
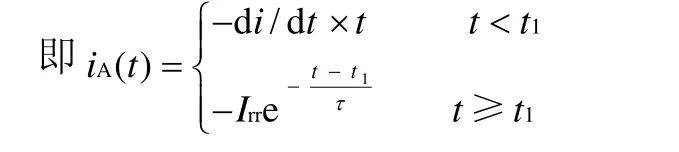
其中, t1为反向恢复电流峰值的时刻,τ为指数时间常数。
很明显,如果采用指数函数的恢复电流模型,直接求解阻容吸收电路的微分方程是比较繁琐的,然而利用计算机仿真则能够很好的解决这个问题。
2 具有动态恢复特性的晶闸管模型
目前,虽然有人提出了晶闸管反向恢复等值电路的仿真方法,然而大多仅仅是局限于后半部分的局部仿真,不是整个恢复过程的仿真,不能动态反映晶闸管的反向恢复特性。另外,也有人介绍了一些微观宏观相结合的晶闸管宏模型[6-8],利用电容的充放电特性来模拟反向恢复过程,其控制方式比较复杂,难以实现精确模拟,不便于工程直接应用。所以,建立一种动态的晶闸管反向恢复模型是非常必要的。
为了使模型具有良好的通用性和进一步推广,在此选择工程应用非常广泛的Matlab软件作为建模仿真工具,更具有典型意义。对于其他仿真软件来说,可作类似的设计。
由于Matlab电力系统工具箱中的晶闸管模块并不包括反向恢复过程,仅仅是考虑了关断时间。为了能够准确完整地反映出晶闸管的反向恢复特性,并能直接应用于晶闸管整流电路的仿真,经过多次的努力尝试,在内置晶闸管模块的基础上作了进一步的开发设计,另外添加反向恢复电流的补充模块及其控制模块,最终成功建立了一种具有动态反向恢复特性的晶闸管模型[9]。该模型主要采用了以下技术方法:
(1)采用数学函数直接生成恢复电流。根据厂家提供的元件关断特性曲线,拟合计算恢复电荷Qrr和恢复电流Irr,从而保证了模型的动态参数与特性曲线是完全一致的,具有很强的针对性。
(2)反向恢复电流的数学模型采用指数函数,有效克服了突然截止模型的不足。当然也可以根据不同器件特性选择其他数学模型,具有极好的灵活性。
(3)能够根据外电路的电流变化率 di/dt实时计算反向恢复电流的峰值和反向恢复电荷的大小,是对整个反向恢复过程的动态模拟,可以直接应用到更加复杂的整流仿真电路中,具有良好的适应性。
该模型的仿真波形如图1所示。
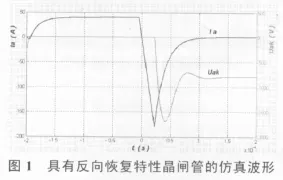
3 晶闸管RC吸收电路的仿真
为了能够对晶闸管阻容吸收电路的内在规律有一个基本的认识,在此主要研究单个晶闸管阻容吸收电路的仿真计算。下面以 ABB公司的晶闸管5STP34Q5200在某工程的应用为例,利用具有动态恢复特性的晶闸管模型搭建仿真电路如图2所示。
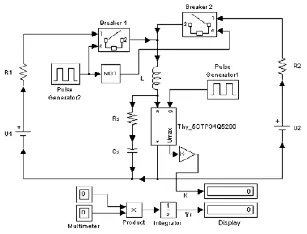
图2 晶闸管RC吸收回路的仿真电路
在此仿真电路中:电压源U1提供正向电压;电压源 U2提供反向电压;R1和 R2为线路电阻,L为线路电感,Rs、Cs为吸收电路。脉冲发生器1提供触发脉冲,脉冲发生器2控制两个开关的状态。首先开关1闭合,开关2断开,晶闸管承受正向电压触发导通。然后开关1断开,开关2闭合,晶闸管承受反向电压而关断。晶闸管模型采用指数恢复模型,根据提供的反向恢复特性曲线建立。
参考某一实际工程,电路的主要参数如下:U1=1000V,R1=1Ω,U2=-1438V,R2=0.001Ω,L=100µH。仿真算法采用ode15s,步长为1e-6s。
对于实际的工程来说,反向电压U2和回路总的折算电感L一般是既定的,晶闸管的恢复特性曲线也是既定的,因此研究的重点就是Rs、Cs与过电压倍数K、电阻损耗Wr之间的变化规律。只要给出吸收电路Rs和Cs的值,利用以上的仿真电路,通过仿真就可以方便地得到此阻容参数条件下的恢复过电压倍数K和反向恢复过程Rs消耗的能量。
4 吸收电阻的参数设计
为了研究吸收电阻Rs与吸收电容Cs、过电压倍数K、电阻损耗Wr之间的变化规律,把Rs从1Ω到20Ω每隔0.5Ω取一个值,Cs从1µF到10µF每隔1µF取一个值,通过以上的仿真方法,得到每个组合参数条件下的恢复过电压倍数和Rs消耗能量的全部数据。
以吸收电阻Rs为横坐标,以过电压倍数K为纵坐标的关系曲线如图3所示。
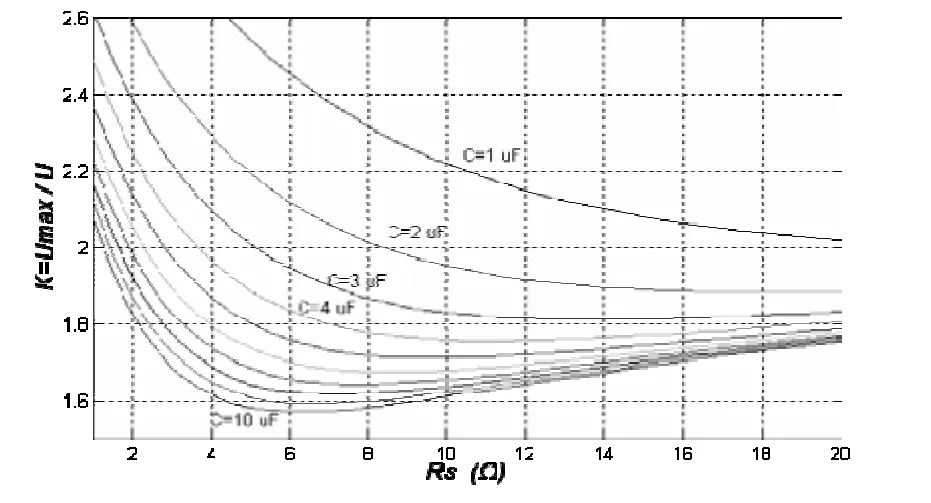
图3 吸收电阻Rs与过电压倍数K的关系曲线
以吸收电阻Rs为横坐标,以电阻损耗Wr为纵坐标的关系曲线如图4所示。
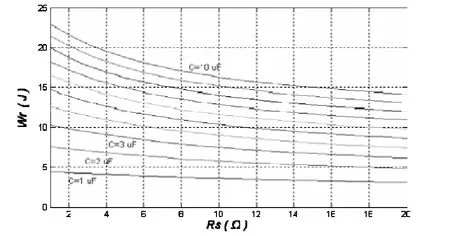
图4 吸收电阻与电阻损耗的关系曲线
由图3的关系曲线可以看出:在相同的Cs参数条件下,存在一个最佳的Rs值与关系曲线的最低点相对应,并且惟一,此时过电压倍数最小,吸收效果最佳。例如:当Cs=10µF时,在Rs=6.5Ω处K=1.572取得最小值,吸收效果最佳。因此,设计的关键是如何找到这个电阻值,以便达到最佳吸收的目标。
例如:当Cs=10µF时,
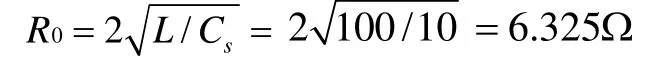
可以看出,Rs的值与R0的值非常接近。
再如:当Cs=4µF时,
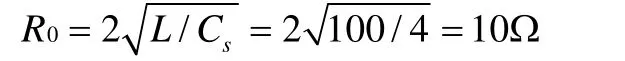
由图3的关系曲线可以看出,在Rs=10.5Ω处K=1.758取得最小值,吸收效果最佳。
所以,可以得出这样的结论:当Rs取值在R0附近时吸收效果最佳。为简便起见,Rs的取值与R0相等,即:
这是设计吸收电阻应考虑的一个重要原则。
5 吸收电容的设计
同样的,由图3过电压关系曲线可以明显地看出,电容Cs对过电压倍数K的影响是比较大的,并且两者是多值对应的关系。另外,从图4电阻损耗关系曲线还可以发现,电阻损耗Wr与Cs的大小关系很大,基本上是线性关系,Rs的大小对Wr的影响非常有限,当Rs增大到一定程度时,电阻损耗Wr的变化也就趋于非常平缓了。
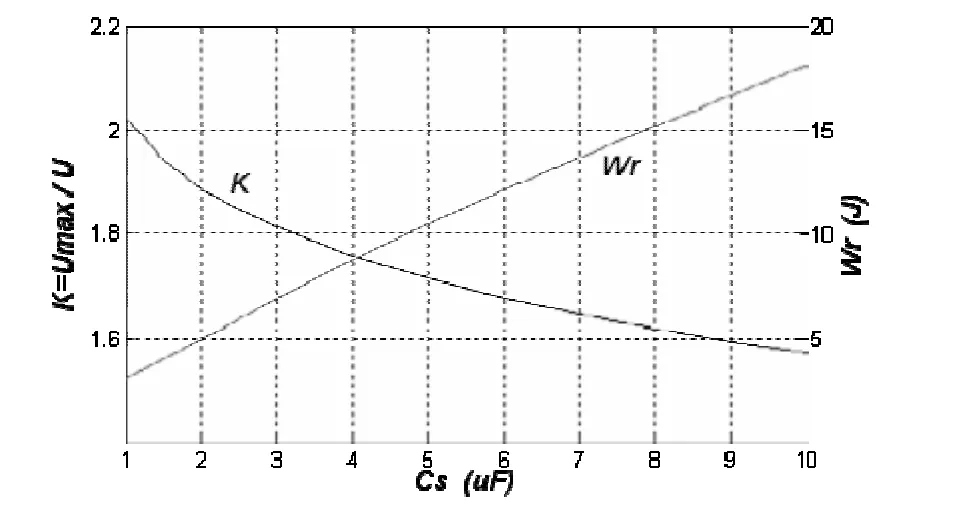
图5 吸收电容与过电压倍数、电阻损耗的关系曲线
从图5可以看出,随着吸收电容Cs的增大,过电压倍数K相应降低,当Cs增大到一定程度后,过电压倍数K的变化趋于平缓,这说明过大的Cs对大幅降低过电压倍数K的作用不大。另一方面,随着吸收电容Cs的增大,电阻损耗Wr几乎是线性增大的,这说明过大的Cs会直接带来电阻损耗Wr的明显增加,会导致能源的浪费,经济效益变差。
因此,对电容参数的设计应该综合考虑以上两个问题,在过电压倍数K和电阻损耗Wr之间寻求一个合适的平衡点。其中,过电压倍数K是首要的,只有在过电压倍数符合设计要求的前提下,应使得电阻损耗Wr尽量在可以接受的范围内。
这是设计吸收电容应考虑的一个重要原则。
6 阻容吸收电路的设计实例
利用以上两个参数的设计原则,可以设计晶闸管的阻容吸收电路的最佳参数。例如某一实际工程,反向电压峰值U2m=1438V,L=100uH。设计步骤如下:
(1)根据厂家提供的元件数据表,晶闸管5STP34Q5200的额定电压 URRM=4400V,过电压系数K≤URRM/U2m=4400/1438=3.06,考虑适当的裕度,可以取K=1.8为设计目标。
(2)由图 3过电压倍数 K的关系曲线可知Cs=4µF即可满足设计要求。根据吸收电容的参数设计原则,虽然当Cs≥5µF时可以获得更好的过电压抑制效果,但电阻损耗Wr会成比例地升高,因而综合来看Cs=4µF是非常合适的。
(3)根据吸收电阻的参数设计原则,可以得出Rs的参数:
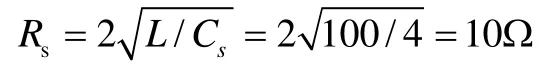
(4)电阻的吸收功率:
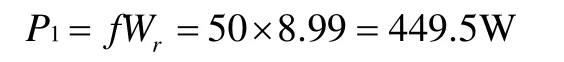
电阻的交流损耗功率:
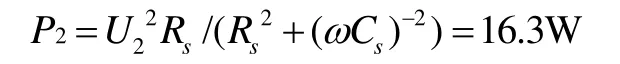
电阻总的损耗功率:
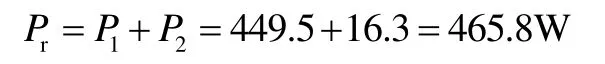
7 现场测试
采用这种动态的指数恢复模型,阻容吸收回路的参数设计不再单纯依靠经验公式和简单推算,而是有了更精确、更直观的设计方法。这为晶闸管阻容吸收的参数设计提供了更加充分的计算依据。利用该方法对晶闸管阻容吸收回路进行参数设计,国网电科院目前已经在多个工程中推广应用,获得了良好的效果。
例如某励磁工程,交流电压峰值为 1258V,利用该方法设计的整流桥阻容吸收参数,其阳极电压的仿真波形如图6所示。
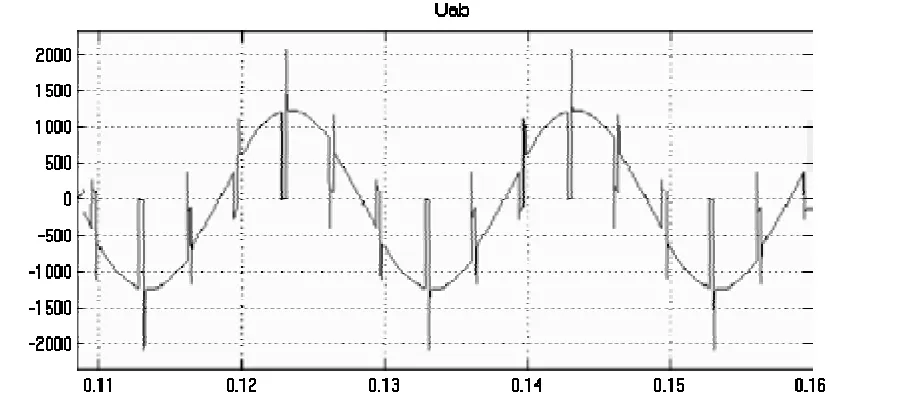
图6 整流桥阳极电压的仿真波形
该工程整流桥阳极电压的现场测试波形如图 7所示。

图7 整流桥阳极电压的现场测试波形
从图中可以看出:仿真波形的过电压尖峰为2076V,现场测试的过电压尖峰为 2160V,过电压倍数仅为1.717;仿真波形与现场测试的基本完全一致,相对误差不到4%,这在工程上是完全可行的。
8 结论
利用指数恢复特性的动态晶闸管模型,对单个晶闸管阻容吸收进行仿真研究,通过改变多种阻容参数的组合,得到了阻容参数与过电压倍数、电阻损耗之间的关系曲线。经过分析研究这些关系曲线的变化规律,得出了吸收电阻和吸收电容的设计原则:当吸收电阻Rs取值在参考电阻R0附近时吸收效果最佳。在过电压倍数符合设计要求的前提下,电容参数应使得电阻损耗Wr尽量在可以接受的范围内。
最后,结合工程实际给出了晶闸管RC吸收回路的参数设计实例。现场测试结果表明:该方法更精确、更实用、更有效。
[1]张明勋.电力电子设备设计和应用手册[M].北京:机械工业出版社,1990:210-211,215-218,262.
[2]刘艳萍,王宝珠,李志军.可控硅换流过程瞬态电压数学模型及其保护参数设计[J].河北工业大学学报,2004,33(5):64-68.
[3]Chang W L,Song B P. Determination of Thyristor Reverse Recovery Current Parameters. IEEE Proceedings.1988, 135(2):91-96.
[4]Rahul S C, Eric I C. A snubber design tool for P-N junction reverse recovery using a more accurate simulation of the reverse recovery waveform[J]. IEEE Transactions on Industry Applications.1991,27(1):74-84.
[5]Cliff L M,P O Lauritzen.A Physically-based Lumped-Charge SCR Model.IEEE.1993:53-59.
[6]邹刚,陈祥训,郑健超.用于电力电子系统暂态过程分析的晶闸管宏模型.中国电机工程学报,1999(6):1-5.
[7]邹刚,陈祥训,郑健超.一种微观宏观相结合的晶闸管PSPICE模型[J].中国电机工程学报,1999(7):6-10.
[8]温家良,刘正之,傅鹏.一种简化晶闸管宏模型及其在暂态分析中的应用[J].电力电子技术,2002(2):66-68.
[9]郝勇,许其品,曾继伦等. 晶闸管换相过电压的Matlab仿真[J]. 水电厂自动化, 2007(4):195-199.

