最小二乘法在PCB板厚控制中的应用

杨荣福

（厦门荣厦机电工程有限公司，福建厦门361009）

中国的PCB产量已居世界第一，但仍是PCB进口国家，所以PCB工业要向更深层次发展，才能满足我国信息产业的要求。现在面临的挑战为：转型、成本和环保方面三大主题[1]。具体到制造过程中，就是要提高PCB的制造精度，降低成本。这需要制造技术人员改善工艺，进行测试实验，分析实验所得数据，这些就成为工艺技术人员和品质检验人员工作的重点。而最小二乘法是科研人员和工程人员最普遍使用的方法之一，若用手算实现，则非常复杂，当用Excel和MATLAB实现起来，则轻松简单了。本文以PCB板厚估计的曲线拟合为例，说明了最小二乘法与Excel及MATLAB结合在PCB制造过程中的应用。

1 最小二乘法基本原理

在对试验数据统计分析研究工作中，常需从一组观测数据

（xi,yi）（i=1,2…,N）中，

求得变量x与y之间的某种近似关系y=φ（x）。

从几何图形上看，就是根据N个给定的点（xi,yi）（i=1,2…,N）求一条近似曲线，由于一般实验数据很多，而且观测数据本身还有误差，因此所求的曲线不要求过所有的给定点（xi,yi），即不要求

而只要求函数y=φ（x）能反映数据的基本变化趋势，满足

按这样确定的更一般的提法是：对于给定的数据

（xi,yi）（i=1,2…,N），

选取线性无关的函数族Σφ（xiΣ） 及权函数 ω（x），要求在函数类

φ*（x）=aφ0+aφ1+…+aφm（m ＜ N），使

显然上式是（m+1）个变量a0,a1,…，am的二次函数

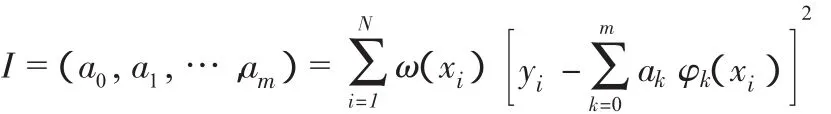
由多元函数极值的必要条件，有

引入内积

方程组就可用矩阵形式表示为

称为法方程，

则可写成

ATWAα=ATWY

由于 φ0,φ1,…,φm线性无关，

法方程存在惟一解

从而得

最小平方误差为

若 φ0,φ1,…，φm还是标准正交系，则

这种方法叫做最小二乘法[2]。

2 PCB板厚估计问题的提出

多层PCB的板厚是其制造过程中品质控制的重要项目，因多层PCB板厚有如下规律[3]：中央厚，四周薄（见图1）。为了所有板厚达到规定范围，则要求制造过程中板面积不能太大，但太小浪费成本，故确定一个合适的面积，是制造前要考虑的。但具体相对中心点各半径处的厚度与半径有何规律，则尚无确定的数量关系。故可做专门的试验，获得原始数据，再用最小二乘法进行曲线拟合，找出二者之间的近似关系函数，在实际产品投入时，就可以此公式计算，从而可在PCB拼版时确定一个合适的面积。

3 最小二乘法在PCB板厚估算中的应用

最小二乘法的使用，是基于所获得的实验数据的。经过对试验PCB板厚的测量，数据见表1，就可以根据这些数据进行最小二乘法做曲线拟合了。下面分别用EXCELL和MATLAB进行实际操作，并进行了结果对比，工程人员可以根据现实状况选择所用的工具。

表1 实验测的板厚数据

3.1 用Excel实现曲线拟合结果

Excel数据处理，就是使用Micro office中的Excel数据处理软件，利用公式和函数对工作表中的数据进行求和、分类汇总和计算。打开Excel文档，先把试验数据填人数据表格中，然后插入图表，并为数据添加趋势线，选择显示公式和显示R的平方值，就可以轻松地得到拟合曲线的公式及平方误差了。取3阶多项式拟合得近似公式

y=-8e-005x3+0.000 8 x2-0.017 5 x+2.016 6，

平方误差

R2=0.998 9。

曲线结果见图2。

图2 Excell拟合结果

图3 Matab拟合结果

3.2 用Matlab实现曲线拟合结果

Matlab是一种功能十分强大、运算效率很高的数学工具软件。在matlab语言中，使用polyfit（X，Y，N）函数来求解最小二乘曲线拟合问题[4]，其中

X，Y为相对应所测数据，N为拟合阶数。

取 X=x0，Y=y0，N=3

求近似公式得

Y=-6.791e-007x3+3.375 3 e-005 x2-0.003 49 x+2.016 6

平方误差δ2=2.784 4 e-005。

曲线结果见图3。

3.3 用Excel和MATLAB实现后的结果比较

通过以上例子可以发现：利用最小二乘法原理与Excel及MATLAB均可计算和画出的曲线清晰美观的关系图，得出近似关系式及平方误差。但两者的结果不相同，由δ2=2.784 4 e-005远小于R2=0.998 9可知，MATLAB编程实现的结果精度要高，Excel则简单方便，直接可以将结果嵌在工作报告里了，在要求精度不高时，得到广泛使用。

4 结束语

PCB制造资料整理，是PCB制造过程中从试验—试验资料整理—提交报告整个环节中，比较重要的一个环节，其好坏直接决定着试验报告的水平和质量。把最小二乘法原理与Excel及MATLAB数据处理工具用在资料整理工作中，将会大大提高工作效率，提高工作质量。

[1]林金堵.中国PCB行业状况与挑战[J].印制电路信息，2009，（1）：16-19.

[2]李 红.数值分析[M].武汉：华中科技大学出版社，2003.

[3]周敏.最新印制电路设计制作工艺与故障诊断、排除技术实用手册[M].吉林：吉林音像出版社，2003.

[4]周金萍.MATLAB6实践与提高[M].河北：中国电力出版社，2001.