输电线路设计覆冰厚度统计模型取用

邹明华，邓洪洲

（同济大学建筑工程系，上海 200092）

输电线路设计覆冰厚度统计模型取用

邹明华，邓洪洲

（同济大学建筑工程系，上海 200092）

0 引言

1998年加拿大魁北克省发生了严重的冰灾，在重灾区魁北克省，1000余座输电铁塔被积累的重冰压倒，400万人没有电力，一些地区整整一个月都没有电，至少25人被冻死[1]。而在2008年1月，我国南方大范围遭遇了有气象记录以来最严重的持续低温雨雪冰冻灾害天气，此次气象灾害对我国西南、华中、华南、华东等地区的电网运行造成了重大危害，造成大范围倒塔、断线和闪络，其中贵州、湖南等地受灾尤为严重，给国民经济和人民生活造成极大的影响,全国范围10～500kV电网因灾停运电力线路数高达36740条，其中停运500kV线路119条、220kV线路348条、110kV线路888条、10～35kV线路35385条，直接经济损失上千亿元。此次遭遇的冰冻强度为50年未见，从现场收集的资料和反馈的信息来看，本次灾害铁塔损毁处导线覆冰的厚度绝大多数超过了30mm，最大达到110mm[2]，大大超过了原设计覆冰厚度，因此科学地确定输电线路设计覆冰厚度对输电线路的安全、经济运营至关重要。

自2008年1月后，相应规范规程得到了修订，规定了设计冰厚750kV、500kV输电线路及其大跨越按50年一遇确定，110～330kV输电线路及其大跨越按30年一遇确定，其中《重覆冰架空输电线路设计技术规程》规定[3]：在有足够的覆冰观测资料，并确认资料有效性的情况下，应采用概率统计法确定线路设计冰厚，其概率模型宜采用极值I型分布。对于目前我国已建或在建的大多数线路来说，相应的覆冰资料尤其是观测的覆冰厚度数据较少，因此规范规定的概率模型宜采用极值I型的准确性值得探讨，为了做到安全可靠、先进适用、经济合理、资源节约、环境友好的要求，有必要对对覆冰荷载的取值进行研究。

表11940 —1999年间Studnice观测站测得的年最大覆冰质量、厚度

1 线路设计覆冰厚度的影响因素

经研究发现，输电线路的设计覆冰厚度的荷载与以下几个因素有关：温度、湿度、风向、风速、地理位置即微地形、测点高度、输电线海拔高度、电线直径、重现期等。设计覆冰荷载可以用单位长度设计覆冰质量W或者设计覆冰厚度t表示，二者的关系如下：

式中，t为设计覆冰厚度，mm；d为导地线直径，mm；W为单位长度设计覆冰质量，(kg·m-1)。

设计覆冰厚度的确定方法如下：

1）收集覆冰观测站冰荷载的观测数据；

2）根据采集到的数据，采用某一概率统计模型，计算一定重现期下覆冰观测站冰荷载；

3）根据观测站标准冰荷载与待建或已建线路冰荷载之间的关系，对一定重现期下观测站冰荷载进行修正，修正因素包括线路海拔高度、电线直径的修正等，得到此线路的设计冰荷载。

在确定一定重现期下覆冰荷载时，采用的概率统计模型甚为重要，采用不同的概率分布模型得到的结果可能差别甚大，而由于地区地形、气候的差异，很难找到一个通用的概率模型进行极值分析，因此，如何采用的覆冰概率统计模型值得研究，由于我国的连续覆冰观测数据较少，下面就捷克Studnice覆冰观测站得到的年最大覆冰值进行分析，以得到不同模型的影响。

2 捷克气象覆冰资料及分析

捷克Studnice观测站1940—1999年间共59a测得的年最大冰重见表1，Studnice位于捷克北部，单位冰重是通过测量离地5m、直径为30mm的水平铁棒得到。由公式（2）转化得到覆冰厚度值，见表1。

下面分别采用正态分布、极值I型Gumbel分布、极值Ⅱ型Frechet分布、极值Ⅲ型Weibull分布对该数据进行了统计分析。

2.1 采用正态分布统计分析

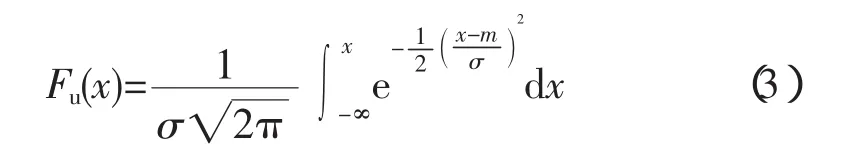
正态分布函数式见式（3），该式中的2个未知参数m和σ采用参数估计采用矩法比较方便。由数学期望和根方差的计算公式得到：

对表1冰厚进行统计分析得其平均值为：

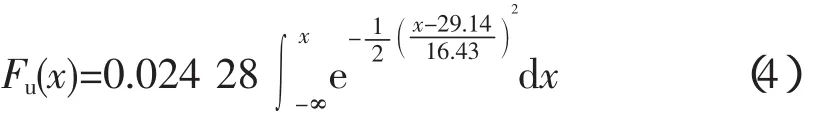
极值I型分布密度为：

由式(4)得到不同重现期下的基本设计冰厚（见表2）。

表2 正态分布不同重现期下的基本设计冰厚

2.2 采用极值I型Gumbel分布统计分析

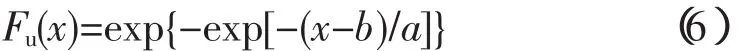
Gumbel分布函数见式（6），该式中有2个未定的参数b和a，其中a为尺寸因子,参数估计采用矩法[8]。由数学期望和根方差的计算公式得到：

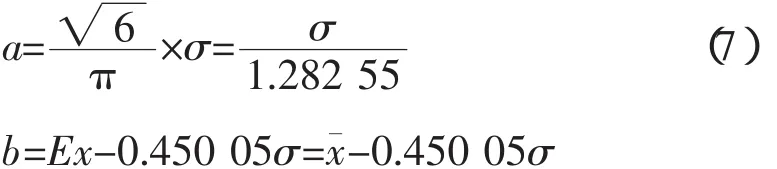
取概率为P0，可以得到：

对表1冰厚进行统计得其平均值为：

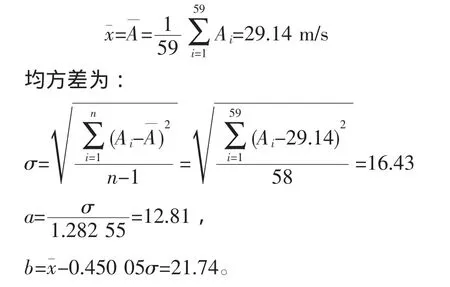
极值I型分布函数为：

求导得极值I型概率密度分布

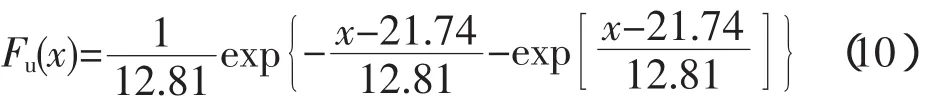
由（8）式算得不同重现期下的设计冰厚（见表3）。

表3 极值I型不同重现期下的基本设计冰厚

2.3 采用极值II型Frechet分布

Frechet分布函数见式（11），该式中有3个待定参数b、a和γ，其中γ为形状参数，a为尺寸因子，可采用和Weibull分布相似的估计方法对3参数的广义Frechet分布进行估计，其中比较常用的是变量替换法，该方法可以得到有效性较高的参数估计值，而且计算起来比较方便[5]。经计算，相关参数的表达式如下：

其中C为欧拉常数，取值C=0.5772。对于b，可先取1个小于xmin的初值，经迭代取1个最优解。

用样本统计量代替式（12）中的E[ln(x-b)]和Var[ln(x-b)]，即可以求得变量γ和a的值。然后由下式计算设计冰厚：

经计算，当a=19.467，b=0.000，γ=2.284时，其拟合优度最好，此时拟合值与实际值的最大偏差：

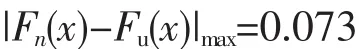
不同重现期下的设计冰厚（见表4）。

表4 极值II型不同重现期下的基本设计冰厚

极值II型的分布函数为

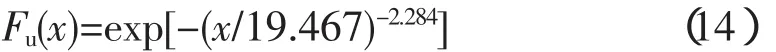
求导后得极值Ⅱ型的概率密度分布函数为：

2.4 采用极值III型Weibull分布

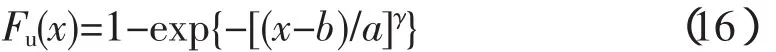
Weibull分布函数见式 （16），对于极值Ⅲ型的Weibull分布也有3个未知的参数，其中γ为形状参数，a为尺寸因子，对于各参数的估计可以参照极值II型的估计方法进行确定。其概率密度分布函数为：

式中，C为欧拉常数，取值C=0.5772。

经计算，当a=27.631,b=4.674,γ=1.496时，其拟合优度最好，此时拟合值与实际值的最大偏差：

不同重现期下的设计冰厚见下表5。

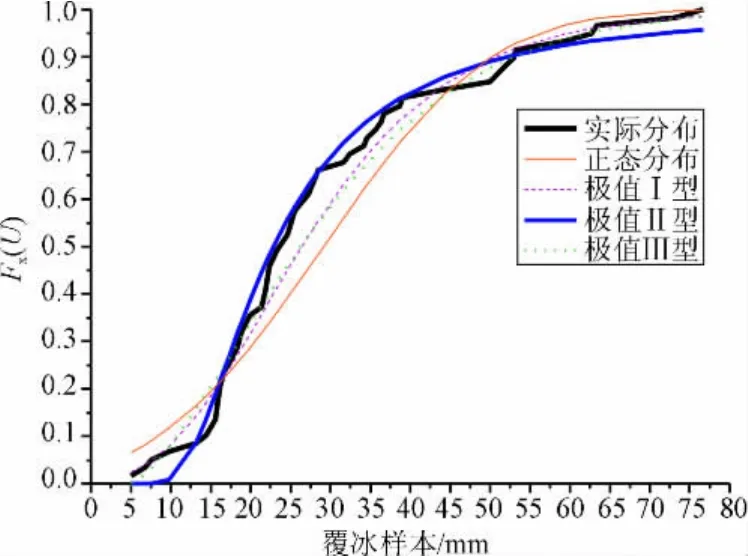
图1为分布函数拟合对比图，可以看出，拟合的最大偏差为DII

表5 极值III型不同重现期下的基本设计冰厚

图1 分布函数拟合对比图

3 各国规范对覆冰模型的陈述

我国 《重覆冰架空输电线路设计技术规程》规定：在有足够的覆冰观测资料，并确认资料有效性的情况下，应采用概率统计法确定线路设计冰厚，其概率模型宜采用极值Ⅰ型分布，即推荐使用极值Ⅰ型分布[6]。

美国ASCE74《guidelines for electrical transmission line structural loading》规定在处理覆冰数据时，使用的词是may be,即极值I型可以用来处理覆冰数据以得到设计覆冰厚度[7],但并非推荐使用该模型。

加拿大使用概率模型确定覆冰厚度时，使用的是IEC60826，IEC60826规定，如果有一个可靠的覆冰模型能估计若干年的最大覆冰荷载，此模型可以用来产生覆冰荷载数据，现场的数据用来校核[8]。

英国BS8100在说明用概率统计模型确定设计覆冰厚度时，也没有说明具体说明采用何种模型，只是说基本设计覆冰厚度r0可以从基于数据基础上的假设数理统计模型中推导得到[9-12]。

从以上分析可以得到，由于微气象等因素的影响，导地线的覆冰非常复杂，因此，在没有足够多的数据支撑条件下，不应确定覆冰荷载的统计模型，故美国ASCE74、IEC60826、英国BS8100规范对覆冰模型的规定比较谨慎，也是比较科学的。相比而言，我国幅员更辽阔，地形气象多样性更显著，而《重覆冰架空输电线路设计技术规程》作为一个行业规范，对覆冰统计模型的规定的科学性值得商讨。

4 结论

综上分析，可以得出以下结论：

1）同一组覆冰数据采用不同的统计分析模型得到的在同一重现期下基本设计覆冰厚度是不同的，甚至差别较大。为了使设计做到安全可靠、经济合理，在采用统计模型时应谨慎。

2）由以上对捷克的数据的分析可以看出，极值II型的拟合度更好，极值Ⅰ型并不是拟合度最好的统计模型,其他国家规范，包括美国、加拿大、英国，也没有明确推荐何种模型。中国地形复杂，气候多样，而《重覆冰架空输电线路设计技术规程》推荐采用极值I型分布，这种规定的合理性值得商榷。

3）基本设计覆冰厚度的概率统计模型应根据实测数据，采用拟合性较好的统计模型，不同的微气象条件下采用不同的概率统计模型，以得到安全经济的设计结果。

[1]Masoud Farzaneh.Atmospheric Icing of Power Networks[M].Canada:Springer Science+Business Media,2008.

[2]李喜来.我国南方地区电网覆冰灾害原因分析及完善措施[C]//输电线路专业委员会输电结构年会，北京：2008.

[3]中华人民共和国国家发展与改革委员会.DL/T 5440-2009重覆冰架空输电线路设计技术规程 [S].北京：中国标准出版社，2009.

[4]陈魁.应用概率分析[M].北京：清华大学出版社,2005.

[5]马开玉.三参数weibull分布参数估计的一种新方法[J].气象科学，1990，10（2）:208-212.

[6]杨靖波,李正,杨风利,等.2008年电网冰灾覆冰及倒塔特征分析[J].电网与清洁能源，2008,24(4):4-8.

[7]Committee on Structural Loading.ASCE74（2005）Guidelines for Electrical Transmission Line Structural Loading[S].USA:ASCE,1991.

[8]International Electrotechnical Commission.IEC60826（2003）Design Criteria of Overhead Transmission Lines[S].Switzerland：HIS，2003.

[9]王琨,谷永刚,彭青宁,等.山区超高压输电线路玻璃绝缘子串防覆冰闪络措施研究 [J].电网与清洁能源，2008,24(8):9-12.

[10]张永飞.福建沿海输电线路设计风速取值探讨[J].防灾减灾工程学报,2009，29(4):411-415.

[11]彭坚,刘强,曹珍崇,等.广西500kV输电线路覆冰倒塔原因分析[J].电网与清洁能源，2008,24(4):9-14.

[12]British Standard Institution.BS8100（1986）Lattice Towers and Masts[S].Britain:BSI,1986.

Study on Probability Distribution Model Of Designed Ice Load For Transmission Lines

ZOU Ming-hua，DENG Hong-zhou
（Department of Building Engineering,Tongji University,Shanghai 200092,China）

Based on the ice load data of Studnice Meteorological Station from1940 to1999, the design ice load ofthe area is calculated and analyzed by normal distribution, Gumbel extreme vaule type I distribution, Frechet extreme vaule type II distribution andWeibull extreme vaule type III distribution respectively. The test result of The Kolmogorov goodness fit λshows that the Frechet extre mevaluetype IIdistributi on is the optimum curvet of iticedistribution of the district. Because of the effect of to pography, the probability distributionmodel differs fromone place to another. The ice load is a key factor of the design of transmission lines toobtain economyand safety, therefore it is suggested that probabilitydistribution model ofice load be chosen based on the records of the sites.

transmission lines；design of ice load;probability distribution model

根据捷克斯洛伐克Studnice覆冰观测站1940—1999年的覆冰观测数据，分别采用正态分布、极值I型Gumbel分布、极值Ⅱ型Frechet分布、极值Ⅲ型Weibull分布对该数据进行了统计分析。由科尔莫戈罗夫-斯米尔诺夫λ拟合度检验结果表明，极值Ⅱ型Frechet分布能较好地拟合该地区的年最大覆冰荷载。由于微地形等因素的影响，线路覆冰厚度的统计分布随地区而异。覆冰厚度是影响冰区输电线路安全、经济的一个重要因素，可根据覆冰观测数据选择概率模型确定设计冰厚。

输电线路；设计覆冰厚度；概率分布模型

国家自然科学基金项目（50078040）。

1674-3814（2010）01-0040-05

TM726

A

2009-10-12。

邹明华（1985—），男，硕士研究生，研究方向为输电线路塔线体系的抗风、抗冰；

邓洪洲（1960—），男，教授，博士生导师，工学博士，主要研究方向为输电塔和结构抗风、抗冰。

（编辑 董小兵）