一种四螺旋混沌系统仿真研究★
吴国增
(聊城大学东昌学院 山东聊城 252000)
0 引言
混沌现象广泛存在于电子学、物理学、化学、生物学以及技术科学、社会科学等各个领域[1]。混沌信号具有丰富的非线性动力学特征,混沌及其混沌控制在电子系统、保密通信、密码学、流体混合、生物系统、图像数据加密、神经网络等众多领域中得到了广泛的应用[2]。
采用线性反馈控制方法控制混沌Lorenz系统[3], 陈关荣等人在1999 年发现了一种与混沌Lorenz系统类似但不拓扑等价的混沌Chen 系统后[4],引起了研究者寻找新的混沌系统并对其非线性动力学现象和应用等研究的极大兴趣。2002年,吕金虎等人[5]相继发现了混沌Lü系统和连接Lorenz、Chen和Lü三个混沌系统的统一混沌系统;2003年,L iu等人[6]发现了在三维连续自治混沌系统中能产生四螺旋吸引子的混沌系统。近年来,学者们对这些新的混沌系统的动力学特性、电路实现、控制与同步及混沌应用等诸多方面开展了研究工作,取得了丰富的具有理论意义和实际价值的研究成果[7]。2004年,吕金虎等人基于L iu系统[8]提出了一个新的三维连续自治混沌系统[9],简称新Lü系统,利用一个常数控制器可以使得新系统同时产生两个单螺旋(具有3个平衡点)或双螺旋(具有5个平衡点)的奇异吸引子;也可以利用一个常数控制器把两个双螺旋的上吸引子和下吸引子无缝连接起来,得到一个四螺旋的奇异吸引子。作者首先基于新Lü系统,采用线性反馈控制的方法,构建一个新四维连续自治耗散混沌系统;其次运用数值仿真手段对新系统进行详细的动力学特性的研究;最后设计一个新系统的实验电路,并进行相应的电路仿真验证。
1 四螺旋鲁棒混沌吸引子
200 4 年吕金虎等人提出的新Lü系统的动力学常微分方程组可以描述为:
Dx/dt = - [ab / (a + b)]x - yz
Dy/dt = ay + xz
Dz/dt = bz + xy
其中, a和b为负实数,设a = - 10, b = - 4,当初始值为(x0, y0, z0) 且z0 > 0时,系统(1) 能生成一个双螺旋上吸引子;当初始值为(x0, y0, z0) 且 z0<0时,系统(1) 能生成一个双螺旋下吸引子。
基于系统(1) , 添加一维由线性方程式组成的控制器,反馈到第二方程式上,可以构造出一个新的4阶混沌系统(2)如下:
Dx/dt = - [ab / (a + b)]x - yz
Dy/dt = ay + xz +w
Dz/dt = bz + xy
Dw/dt = c (z +w )
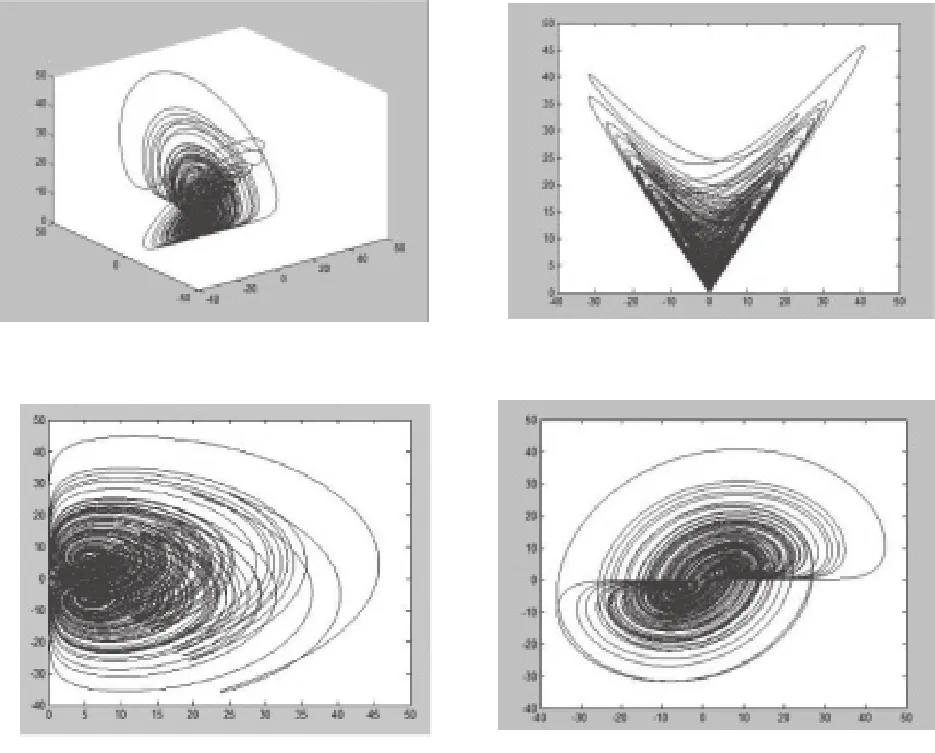
图1 系统(1)吸引因子仿真图形
其中, c为一个负实数。当a = - 1 0, b = - 4和c =- 5时,系统(2) 是混沌的, 产生了奇异的四螺旋混沌吸引子,如图1所示。这里,初始值为(10, 10,10,0) ,其Lyapunov指数为L E1 = 1. 0312, L E2 = 0,L E3 = - 4. 6811, L E4 = - 12. 4739,相应的在x =0截面上的庞加莱映射如图2 (a) 所示,可以看到混沌吸引子的截面有着更多的折叠;图2 (b) 则示出了该系统(2) 的x (t) 时域波形, 它是非周期的, 可以发现系统(2) 的吸引子有着更复杂的拓扑结构。

图2 系统(2)吸引因子仿真图形
从图2双螺旋混沌吸引子的相轨图可以观察出:(a) 在x - y平面上, 双螺旋吸引子只保留了四螺旋吸引子在x = y直线方向上的吸引子; (b) 在x- w平面上,双螺旋吸引子只保留了四螺旋吸引子的下吸引子; (c) 在y - z平面上,双螺旋吸引子只保留了四螺旋吸引子的上吸引子; (d) 而在z - w平面上,双螺旋吸引子只保留了四螺旋吸引子的下右吸引子。

图3 lyapunov指数
从图3中可以观察到,系统(2)的最大Lyapunov指数有三个 始终大于零,且变化区间内几乎恒等不变, 这意味着系统(2) 具有较良好的混沌鲁棒性。随参数的变化, 系统(2) 的运行状态主要演变历经了以下两种混沌轨道状态,一种是死螺旋的一种是双螺旋的。
2 电路仿真
本文所提出的四维自治混沌系统的实验电路原理图如图4所示。
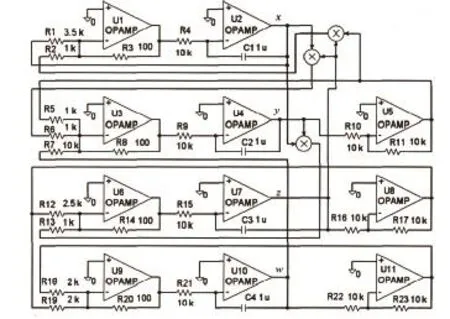
图4 电路图
设计思路为在新Lü系统电路上外加一个由加法器、积分器和反相器组成的线性控制器,构成一个由4个状态变量输出的混沌信号发生器电路。电路元器件参数值如图5中所示,运算放大器可采用型号为LF353N等器件,模拟乘法器一般采用AD633器件。
通过调节电阻R20的值来改变新混沌系统电路的参数,利用PSp ice对图5所示电路的瞬态特性进行仿真分析。当R20 = 100Ω时,图5所示混沌系统电路中运算放大器U2与U10输出端的相轨图分别如图6 (a)和(b)所示,其相轨图分别与图1 (b)和图4 (b)相轨图基本一致。

图5 电路仿真图
3 结束语
在新Lü混沌系统上添加线性控制器, 构造出了一个新的混沌系统,能在控制参数变化较大的范围内生成新奇的混沌吸引子。通过计算新系统Lyapunov指数谱,证明新系统的混沌特性具有鲁棒稳定性。随着控制参数逐步改变, 新提出系统由四螺旋混沌吸引子演变成了双螺旋混沌吸引子。MultiSim 10.1电路仿真软件,通过对系统方程构建的相应系统电路进行了实验仿真,其结果表明与理论分析和数值计算的结果具有很好的一致性。
[1]Sajid I, Masood A, SuhailA Q. Investigation of chaotic be2havior in DC2DC converters [J]. Int Journal of Electrical,Computer, and Systems Engineering, 2007, 1(3) : 166 -169.
[2]Donato C, Giuseppe G. Bifurcation and chaotic behavior in boost converters: experimental results [J]. Nonlinear Dy2 namics, 2006, 44: 251-262.
[3]L iu Z, Zhu X H, HuW, et al. Princip les of chaotic signal radar [J]. Int J Bifur Chaos, 2007, 17 (5) : 1735-1739.
[4]Bao Bocheng, Xu J ianp ing, L iu Zhong. Study on stability control of ramp compensation for switched DC2DC converter [J]. Journal of University of Electronic Science and Tech2 nology of China, 2008, 37(3) : 397-400.
[4]包伯成,许建平,刘中. 开关DC2DC变换器斜坡补偿的稳定性控制研究[J]. 电子科技大学学报, 2008,37 (3) : 397-400.
[5]Venkatasubramanian V, Leung H. A novel chaos2based high2resolution imaging technique and its app lication to through2the2wall imaging [J]. IEEE Sign Process Lett,2005, 12: 528-531.
[6]Abel A, Schwarz W. Chaos communications2Princip les, schemes, and system analysis [J]. Proc IEEE, 2002,90: 230.
[7]Stewart I. The Lorenz attractor exists [J]. Nature,2002,406: 948-949.
[8]Chen G,Ueta T. Yet anthor chaotic attractor [J]. Int J Bi2 fur Chaos, 1999, 9 (6) : 1465-1466.
[9]Ueta T, Chen G. Bifurcation analysis of Chen’s attractor[J]. Int J Bifur Chaos, 2000, 10: 1917-1931.

