基于时域滤波互谱密度的扩频信号测向

李 钢,贾 峰

(1.中国电子科技集团公司第五十四研究所,河北石家庄050081;2.空军驻石家庄地区军事代表室,河北石家庄050081)

0 引言

直接序列扩频信号具有良好的低功率谱密度发射带来的隐蔽性,伪随机编码所带来的保密能力和信号相关处理所带来的抗干扰能力等优点,在现代通信系统,尤其是军事通信系统中的应用日益广泛。随着扩频信号在通信中应用的迅猛发展,在电子对抗中必须研究如何侦测和截获扩频信号。

基于相位测量和幅度相位测量的测向体制,如干涉仪、空间谱估计,前提条件之一是信号为窄带,直扩信号利用高速率伪随机码对数据进行调制,将信号带宽大大扩展,此时测向已无法直接应用上述算法,而必须增加预处理,实现起来比较复杂。基于时差测量的测向体制,如时差测向,利用到达不同天线单元的时间差测量方位,与频率测量无关,不受信号带宽的限制,具有原理简单、精度高的特点。但受器件等技术水平的限制,国内尚未将时差测向技术应用于实际工程。

时域滤波互谱密度法是一种适用于扩谱信号侦测的技术,通过对2路空间分离的天线接收信号进行互相关处理,并对零时间偏移附近很窄范围内的互相关函数加窗处理和傅里叶变换,形成时域滤波互谱密度,检测到扩频信号并确定带宽后,可以通过测量信号带宽内的相位斜率来估计信号到达方位。

1 时域滤波互谱密度法

1.1 系统实现框图

双接收机互相关系统采用2路空间分离的天线和独立接收机以及后处理器组成系统。2部接收机的输出包含信号、天线噪声和接收机内部噪声。其中,接收机的内部噪声相互独立,天线感应的外部噪声虽然同源,但如果这些源发出的信号以不同时延到达2个天线,则可以认为2个天线的输入噪声无关。由于信号与噪声不相关,2路噪声也不相关,所以噪声分量会均匀地分布于相关器输出的整个宽度内。系统中2路接收机同时通过天线接收信号经过转换后输出生成互相关函数具有宽带特性,而信号分量即扩频信号的窄自相关函数却主要集中在零点附近,一般扩频信号可以通过对互相关器输出峰值进行门限判决就可以在时域检测有无扩频信号。检测到扩谱信号后可以根据信号的幅度相位信息估计来波方向。

双接收机互相关系统组成如图1所示。图1中,d为基线长度;θ为信号的到达方向;td为信号到达2个天线的时间差;c为光速;ctd为波程差。

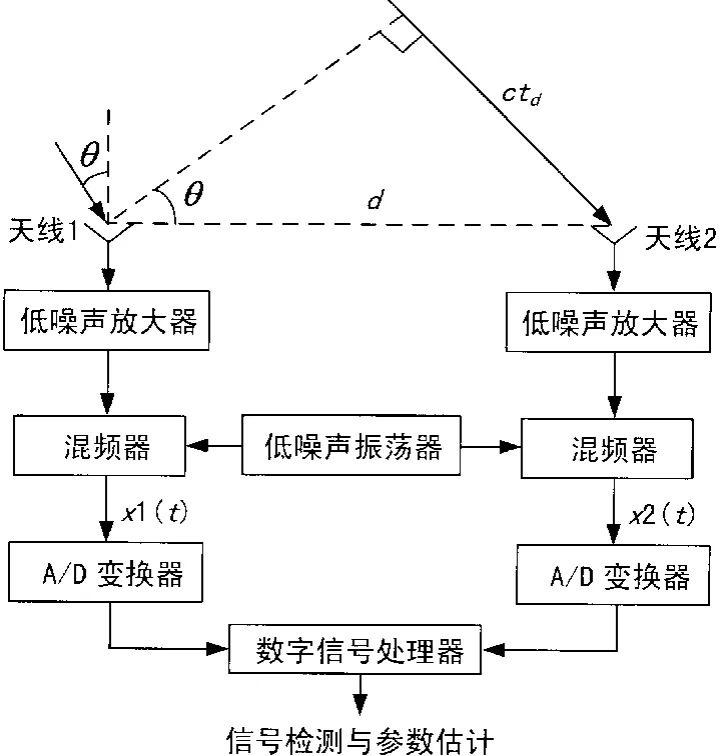
图1 双接收机互相关系统简化框图

1.2 数学模型

双接收机互相关系统是基于2个天线的输入噪声无关的基础上建立的,系统要求2个天线的距离足够大,2路噪声可视为不相关。这里讨论的扩频信号条件仅限于比较简单的单信号源情况,此时,2路观测数据x1(t)、x2(t)的互相关函数等于信号的自相关函数加上噪声,即

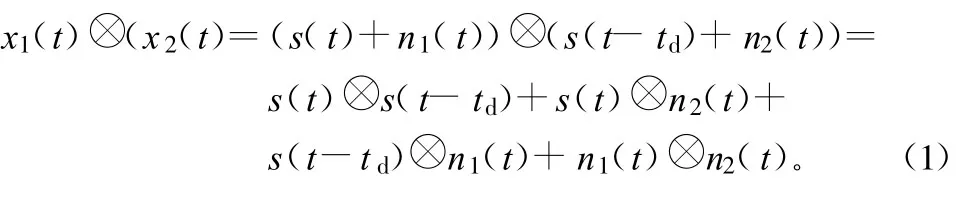
式中,⊗表示互相关。

互相关函数中的信号部分等于扩频信号的时移自相关函数,信号带宽越宽,自相关函数越窄,而互相关函数中的噪声部分则均匀散布于全部时间宽度,如果使用一个时域滤波器选取互相关函数中心很窄的一部分,可以捕获全部信号,而抑制绝大多数噪声。对加窗互相关函数进行傅里叶变换,产生时域滤波互谱密度,通过门限检测可以检测扩频信号的存在,并有可能根据时域滤波互谱密度在信号带宽内的相位谱斜率估计到达方向。

2 扩频信号的检测和测向

2.1 扩频信号检测

扩频信号检测主要是计算相关器的输出SNR的值,通过门限检测比对得出扩频信号是否存在。由式(1)可知,相关器输出互相关函数的第1项是信号自相关函数,后3项是噪声部分,包括2个信号—噪声互相关和一个噪声 — 噪声互相关,对于低信噪比(SNR＜0 dB)情况,噪声 —噪声互相关起决定作用。如果相关器2个输入的噪声相同,则噪声自相关函数会在相关函数中心处呈现大而窄的峰值,根据上一节关于噪声的假设条件,相关器的2个输入噪声无关,其相关函数不存在这样的峰值。

经推导,相关器的输出SNR等于:

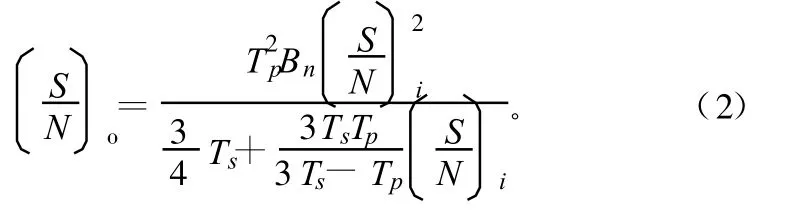
式中,(S/N)i为相关器的输入SNR;Bn为接收机带宽;Bs为信号带宽;Ts为采样时间;Tp为信号持续时间,对于CW信号,Ts≡Tp,此时,式(2)可简化为:

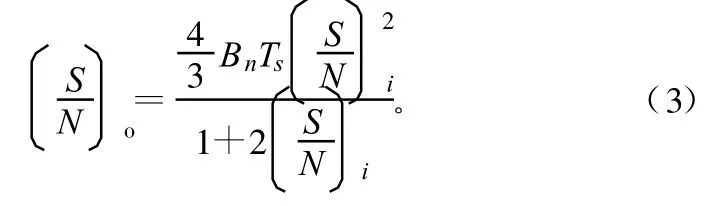
离散傅里叶变换视其采样信号为周期连续信号的一个时间周期,因此基于FFT的相关器输出不同于有限采样时域相关器,后者认为信号采样值是孤立的脉冲,时域相关器的输出长度是2Ts,而基于FFT相关器的输出长度是Ts,另外,噪声 — 噪声互相关、信号 —噪声互相关的幅度包络亦不相同,类似地,可得基于FFT相关器的输出SNR为:

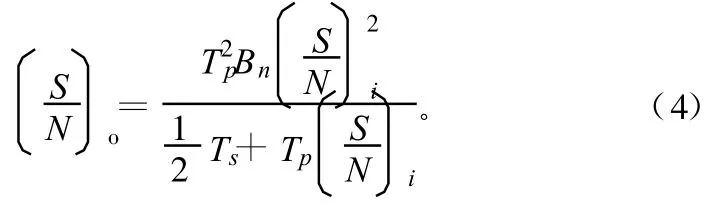
对于CW信号,式(4)可简化为:

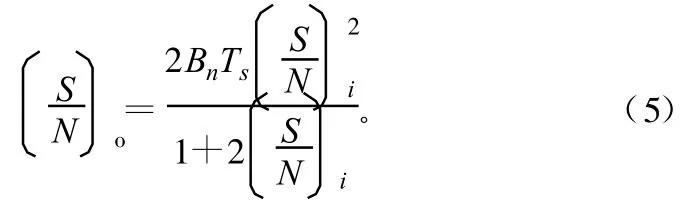
对互相关函数求傅里叶变换,得到互谱密度,此时互谱密度的输出SNR为:

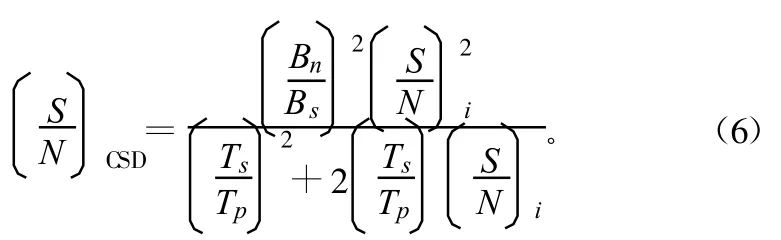
对于CW信号,式(6)可简化为:

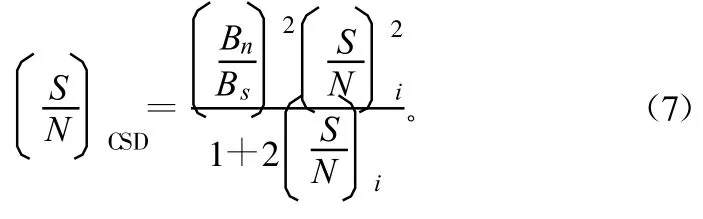
对互相关函数时域加窗后,求付里叶变换,得到时域滤波互谱密度。对CW信号时域滤波互谱密度的输出SNR为:

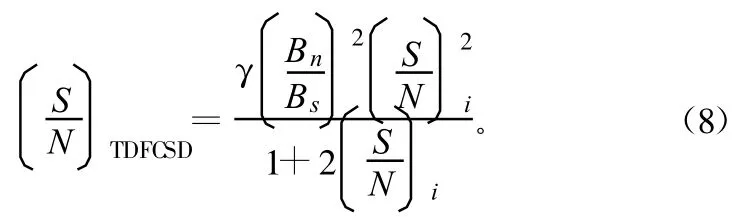
式中,γ为放大因子,

2.2 扩频信号测向

扩频信号的测向是通过测量信号自相关函数位置的方法可以实现测向,该位置相对于互相关函数中心的时间偏移等于信号入射到2个天线单元的时间差,但是当基线较短时,直接由互相关函数估计时间差是不现实的。考虑没有任何先验信息的情况,根据时域滤波互谱密度的相位斜率估计到达时差,即时域中的时间偏移对应于频域中的线性相位斜率为:

利用线性回归法拟合时域滤波互谱密度相位谱的一组点,即可估计出时域滤波互谱密度的相位斜率m,进而计算时差:

根据时差测向公式:

得到只考虑时间差测量误差引起的测向误差为:

进一步得出时域滤波互谱密度法估计方向 θ的方差为:

3 仿真试验及结果分析

3.1 仿真试验

利用扩频信号中典型的chirp信号和BPSK两种样式的信号通过计算机仿真对时域滤波互谱密度测向算法进行验证。

chirp信号方针条件为信号频率在500 μ s的时间内从50MHz扫描到70MHz,信号带宽为20MHz,假设接收机噪声带宽100 MHz。入射方位角21°。信噪比0 dB。通过仿真可以得出chirp信号的互相关函数,2路信号之间具有很强的相关性,当信号之间的延时量取-10 ns时,相关函数出现峰值,在实际信号方位角=22.7°,SNR=6 dB的条件下方位角估计值为23.14°。图2中给出在上述条件下chirp信号的时域滤波互谱密度的幅度、相位和去弯折后的相位信息。

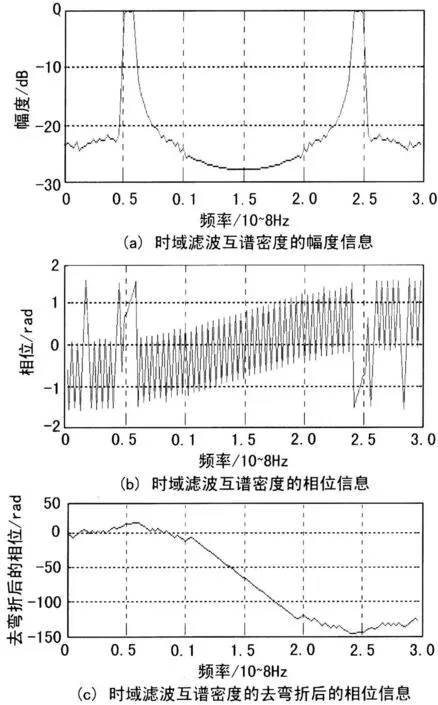
图2 chirp信号的时域滤波互谱密度

对BPSK信号进行仿真,在BPSK信号的码速率为10 MHz,接收机噪声带宽100 MHz,假设BPSK信号的入射方位角为33.6°,SNR=6 dB,通过仿真计算方位角估计值为32.28°。

3.2 结果分析

针对chirp信号在不同信噪比条件下对其进一步仿真,得到输入信噪比与测向精度的关系如图3所示,当信噪比在-5 dB以上时,算法较为稳定,测向精度较好,能够满足一般工程使用。信噪比在-5 dB以下时,性能恶化。

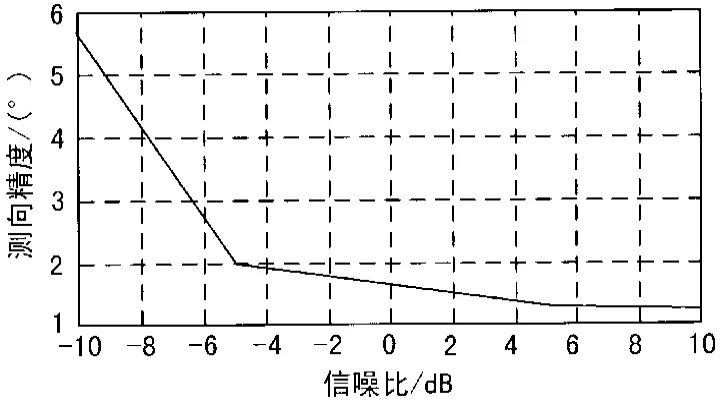
图3 时域滤波互谱密度法测向精度与输入SNR的关系

4 结束语

理论分析和仿真试验表明,基于阵列天线各路信号之间强相关性推导出的时域滤波互谱密度函数,对于较低信噪比下的扩频信号的检测和测向具有良好的性能。当互谱密度超过检测门限时,认为发现信号,此时信号带宽越宽,测向精度越高,对于带宽越宽的扩频信号检测概率和测向精度则更高。文中仅仅考虑了单信号情况,多信号的检测和测向是下一步的研究内容。

[1]HOUGHTON A W,REEVE C D,Detection of Spread-Spectrum Signalsusing the Time-Domain Filtered cross Spectral Density[J].IEE Proc.-Radar,Sonar Navig.,1995,142(6):286-292.

[2]HOUGHTON A W,REEVE C D,Direction Finding on Spread-Spectrum Signals using the Time-Domain Filtered cross Spectral Density[J].IEE Proc.-Radar,Sonar Navig.,1997,144(6):315-320.

[3]山娟苗,张海瑛.直扩信号的相关函数包络检测法[J].无线电工程,2006,36(6):16-18.